数据结构 C语言实现霍夫曼树的编码译码详解

数据结构 C语言实现霍夫曼树的构造及编码译码详解

本代码数据结构很特别，借鉴了某位大佬的霍夫曼数据结构
写的比较复杂，编码为makecode2函数，译码为decode函数，本人原创嘻嘻

本人是双非大二混子，学习方向为机器学习，云计算，欢迎大家私信交流

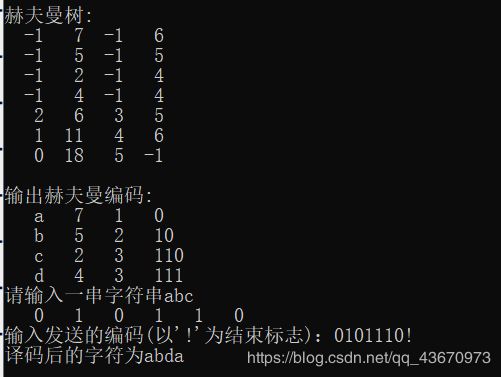
下面对部分结构进行超级详细解析 ：下图为本次代码的霍夫曼树

本代码霍夫曼树均存放权值，按照权值进行树结点的标号排序
（下图赫夫曼树第二列 权值为7是a，5是b，2是c，4是d，）

这里我要解释一下，这个赫夫曼树存放的是他的权值，-1就表示空的，木有东西，下面代码有注释 然后按照tree[]数组结点标号，temp[] 这个数组依次存的是字符a，b，c，d，标号以此为0，1，2，3.所以temp[]的四位和tree[]前四位标号对应的字母应该是一致的，这在编码译码就起到了巨大作用。见上面小黑图的赫夫曼树第二列 7是0号位，18就是6号位在decode译码中，需要理解i=6是什么含义哦我要解释的就这么多，废话不多说，看代码（数据结构比较复杂，代码逻辑晦涩难懂（别担心，注释很多），好事多磨，我也是大二学生，一起噶油啊！

/*
实现对赫夫曼编码主要步骤：
生成一个节点数组用来存放树的节点信息
初始化
从中找出权值最小和权值次小节点然后生成这两个节点的双亲节点权值最小节点是该双亲节点的左孩子次小为右孩子然后将该双亲节点加入到节点数组中并标记为已加入
重复三步骤直到赫夫曼树构造成功
*/
#include
#include
#define LEN_CODE sizeof(HaffmanCode)
#define LEN_NODE sizeof(haffmannode)
#define MAXWEIGHT 1000  //用来存储最大的权值数
#define MaxBits 30      //用来存储转化后的编码
#define MaxNodes 30     //总节点数

typedef struct HaffManTree
{
    int weight;                         //存放节点的权值
    int LeftChild,RightChild,Parent;    //采用仿真指针方法存放节点的左右孩子和双亲下标
    int flag;           //用来判断该节点是否已经加入了赫夫曼树中(0表示未加入，1表示已经加入 )
}haffmannode;

typedef struct HaffMancode
{
    int bits[MaxBits];  //用来存放赫夫曼编码
    int weight;         //用来存放对应的权值
    int length;         //赫夫曼编码长度
}HaffmanCode;

void MakeTree(int weight[],int n,haffmannode haffmantree[]);
void MakeCode(haffmannode haffmantree[],int n,HaffmanCode haffmancode[]);
void DispCode(char temp[],haffmannode tree[],HaffmanCode Code[],int n);


/*功能函数的实现*/
void MakeTree(int weight[],int n,haffmannode haffmantree[])
{
    int i,j,m1,m2,x1,x2;
    //初始化（n个叶节点一共 2*n-1 个节点）
    for(i=0;i < 2*n-1; i++)
    {
        if(i < n)  //处理 n 个叶子节点
            haffmantree[i].weight=weight[i];
        else
            haffmantree[i].weight=0;

        haffmantree[i].LeftChild=-1;  //开始时候让左右孩子和双亲的下标为 -1
        haffmantree[i].RightChild=-1;
        haffmantree[i].Parent=-1;
        haffmantree[i].flag=0;
    }

    //每次从中选出权值最小的和次小的构成树的左右子树
    //处理 n-1 个非叶子节点
    for(i=0; i<n-1;i++)
    {
        m1=m2=MAXWEIGHT;
        x1=x2=0;
        //从有权值的节点中查找 m1 用来存放权值最小的 m2 用来存放权值次小的 x1 用来存放权值最小的下标 x2 用来存放权值次小的下标
        for(j=0;j < n+i; j++)
        {
            if(haffmantree[j].weight < m1 && haffmantree[j].flag==0)
            {
                m2=m1;
                x2=x1;
                m1=haffmantree[j].weight;
                x1=j;
            }
            else if(haffmantree[j].weight < m2 && haffmantree[j].flag==0)
            {
                m2=haffmantree[j].weight;
                x2=j;
            }
        }
        haffmantree[x1].Parent=n+i; // 比如第一个双亲节点的下标就是 n 第二个双亲节点的下标就是 n+1 --------
        haffmantree[x2].Parent=n+i;
        haffmantree[x1].flag=1;
        haffmantree[x2].flag=1;
        haffmantree[n+i].weight=haffmantree[x1].weight + haffmantree[x2].weight;  //权值求和
        haffmantree[n+i].LeftChild=x1;
        haffmantree[n+i].RightChild=x2;
    }
}

//本函数用来实现对赫夫曼编码的解决
void MakeCode(haffmannode haffmantree[],int n,HaffmanCode haffmancode[])
{
    int i,j;
    int Child,Parent;
    HaffmanCode *code;
    code=(HaffmanCode *)malloc(LEN_CODE);  //用来存放临时数据
    for(i=0;i < n ;i++)
    {
        code->weight=haffmantree[i].weight;
        code->length=0;
        Child=i;
        Parent=haffmantree[Child].Parent;
        while(Parent != -1) //当双亲节点不为根节点时候
        {
            if(haffmantree[Parent].LeftChild==Child)  //如果当前节点是双亲节点的左孩子就将0加入到该编码中，如果是右孩子就将1加入到编码中
                code->bits[code->length]=0;
            else
                code->bits[code->length]=1;
            code->length++;
            Child=Parent;               //自底向上移动判断
            Parent=haffmantree[Child].Parent;
        }

        for(j=0;j < code->length;j++) //把该编码加入到对应的编码数组中
            haffmancode[i].bits[j]=code->bits[code->length-1-j];

        haffmancode[i].weight=code->weight; //把对应的权值加入到对应编码数组的权值中去
        haffmancode[i].length=code->length; //将长度复制结构
    }
}


//本函数主要用来实现哈夫曼编码的输出
void DispCode(char temp[],haffmannode tree[],HaffmanCode Code[],int n)
{
    int i,j;
    printf("\n输出赫夫曼编码:\n");
   	for ( i=0;i<n;i++)
	{
        printf("%4c",temp[i]);
		printf("%4d",Code[i].weight);
		printf("%4d   ",Code[i].length);
		for (int j=0;j<Code[i].length;j++)  printf("%d",Code[i].bits[j]);
		printf("\n");
	}
}
void makecode2 (char temp[],haffmannode tree[],HaffmanCode Code[] )
{   
	int i;
	int j;
	int k;
	char s[5];
    printf("请输入一串字符串");
    gets(s);
	i=0;
	while(i<=4)
	{
	  for(j=0;j<4;j++)
	     if (s[i]==temp[j])
          	for (k=0;k<Code[j].length;k++)  printf("%4d",Code[j].bits[k]);
		 
       i++;
	}
	printf("\n");
}
void decode(haffmannode tree[],char temp[])//依次读入电文，根据哈夫曼树译码
{
 int i,j=0;
 char b[100];
     //电文结束标志取!
 i=6;             //从根结点开始往下搜索
 printf("输入发送的编码(以'!'为结束标志)：");
 gets(b);
 printf("译码后的字符为");
 while(b[j]!='!')
 {
  if(b[j]=='0')
   i=tree[i].LeftChild;   //走向左孩子
  else
   i=tree[i].RightChild;   //走向右孩子
  if(tree[i].LeftChild==-1)     //tree[i]是叶结点
  {
   printf("%c",temp[i]);
   i=6;      //回到根结点
  }
  j++;
 }
 printf("\n");
 if(tree[i].LeftChild!=-1&&b[j]!='!')   //电文读完，但尚未到叶子结点
  printf("\nERROR\n");  //输入电文有错
}//decode

int main()
{
    int weight[MaxNodes]={7,5,2,4};
    haffmannode haffmantree[MaxNodes];
    HaffmanCode haffmancode[4];
    char temp[80]="abcd";

    MakeTree(weight,4,haffmantree);

    printf("\n赫夫曼树:\n");
	for (int i=0;i<7;i++)
	{
		printf("%4d",haffmantree[i].LeftChild);
		printf("%4d",haffmantree[i].weight);
		printf("%4d",haffmantree[i].RightChild);
		printf("%4d",haffmantree[i].Parent);
		printf("\n");
	}

    MakeCode (haffmantree,4,haffmancode);
    DispCode (temp,haffmantree,haffmancode,4);
	makecode2(temp,haffmantree,haffmancode);
	decode(haffmantree,temp);
    return 0;
}

结果展示