中文分词器的基本原理和简单实现
对“大学生活”这句话做分词,通常来说,一个分词器会分三步来实现:
- 找到“大学生活”这句话中的全部词做为一个集合,即:[大、大学、大学生、学、学生、生、生活、活]
- 在第一步中得到的集合中找到所有能组合成“大学生活”这句话的子集,即:
[大、学、生、活]
[大、学、生活]
[大、学生、活]
[大学、生、活]
[大学、生活]
[大学生、活]
- 在第二步中产生的所有子集中挑选一个最有可能的作为最终的分词结果。
为了得到第1步需要的集合,通常我们需要一个词典。大部分的分词器都是基于词典去做分词的(也就是说也可以不基于词典来做分词,在此暂时不做讨论)。那么现在假设我们有一个小词典:[大学、大学生、学习、学习机、学生、生气、生活、活着]。首先要在“大学生活”这句话里面匹配到这个词典里面的全部词,有些同学脑中可能会出现这种过程:
public class Demo1{
//加载词典中的所有词汇
static Set dic = new HashSet(){{
add("大学");
add("大学生");
add("学习");
add("学习机");
add("学生");
add("生气");
add("生活");
add("活着");
}};
//匹配句子中词典中存在的所有词汇
static List getAllWordsMatched(String sentence){
List wordList = new ArrayList<>();
for(int index = 0;index < sentence.length();index++){
for(int offset = index+1; offset <= sentence.length();offset++){
String sub = sentence.substring(index,offset);
if(dic.contains(sub)){
wordList.add(sub);
}
}
}
return wordList;
}
public static void main(String[] args){
String sentence = "大学生活";
getAllWordsMatched(sentence).forEach(System.out::println);
}
} 执行这段代码会输出:
大学
大学生
学生
生活似乎到这里,我们已经完美地完成了在词典中找到词的任务。然而真实的分词器的词典往往有几十万甚至几百万的词汇量,使用上面这种算法性能太低了。高效地实现这种匹配的算法有很多,下面简单介绍一种:
AC自动机(Aho-Corasick automaton)
AC自动机是一种常用的多模式匹配算法,基于字典树(trie树)的数据结构和KMP算法的失败指针的思想来实现,有不错的性能并且实现起来非常简单。
字典树(trie树)
引用一下百度百科对于trie树的描述:Trie树,是一种树形结构,是一种哈希树的变种。典型应用是用于统计,排序和保存大量的字符串(但不仅限于字符串),所以经常被搜索引擎系统用于文本词频统计。它的优点是:利用字符串的公共前缀来减少查询时间,最大限度地减少无谓的字符串比较,查询效率比哈希树高。
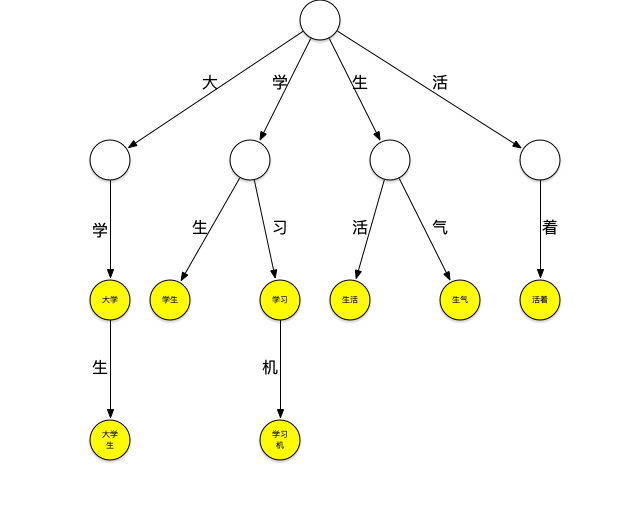
下面一个存放了[大学、大学生、学习、学习机、学生、生气、生活、活着]这个词典的trie树:
它可以看作是用每个词第n个字做第n到第n+1层节点间路径哈希值的哈希树,每个节点是实际要存放的词。
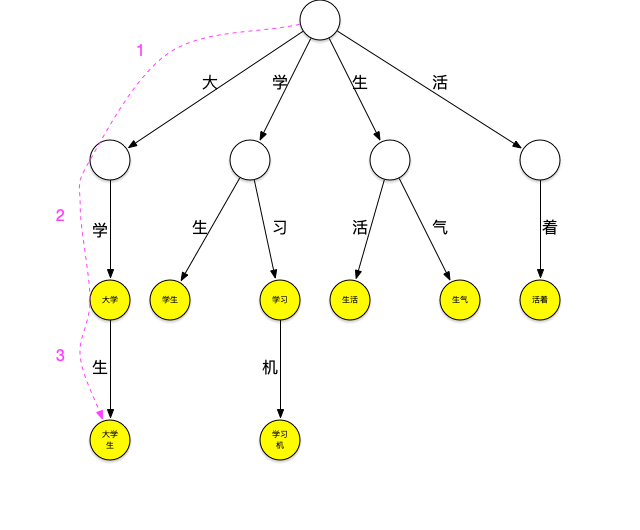
现在用这个树来进行“大学生活”的匹配。依然从“大”字开始匹配,如下图所示:从根节点开始,沿最左边的路径匹配到了大字,沿着“大”节点可以匹配到“大学”,继续匹配则可以匹配到“大学生”,之后字典中再没有以“大”字开头的词,至此已经匹配到了[大学、大学生]第一轮匹配结束。
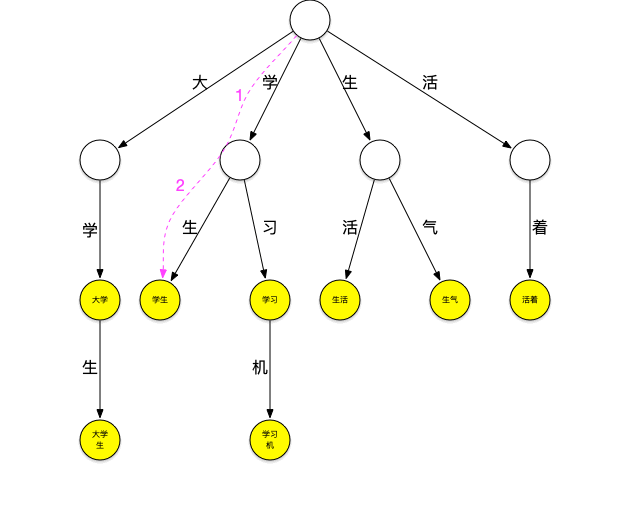
继续匹配“学”字开头的词,方法同上步,可匹配出[学生]
继续匹配“生”和“活”字开头的词,这样“大学生活”在词典中的词全部被查出来。
可以看到,以匹配“大”字开头的词为例,第一种匹配方式需要在词典中查询是否包含“大”、“大学”、“大学”、“大学生活”,共4次查询,而使用trie树查询时当找到“大学生”这个词之后就停止了该轮匹配,减少了匹配的次数,当要匹配的句子越长,这种性能优势就越明显。
失败指针
再来看一下上面的匹配过程,在匹配“大学生”这个词之后,由于词典中不存在其它以“大”字开头的词,本轮结束,将继续匹配以“学”字开头的词,这时,需要再回到根节点继续匹配,如果这个时候“大学生”节点有个指针可以直指向“学生”节点,就可以减少一次查询,类似地,当匹配完“学生”之后如果“学生”节点有个指针可以指向“生活”节点,就又可以减少一次查询。这种当下一层节点无法匹配需要进行跳转的指针就是失败指针,创建好失败指针的树看起来如下图:
图上红色的线就是失败指针,指向的是当下层节点无法匹配时应该跳转到哪个节点继续进行匹配。
失败指针的创建过程通常为:
1.创建好trie树。
2.BFS每一个节点(不能使用DFS,因为每一层节点的失败指针在创建时要确保上一层节点的失败指针全部创建完成)。
3.根节点的子节点的失败指针指向根节点。
4.其它节点查找其父节点的失败指针指向的节点的子节点是否有和该节点字相同的节点,如果有则失败指针指向该节点,如果没有则重复刚才的过程直至找到字相同的节点或根节点。
查询过程如下:
下面简单实现做了一个AC自动机的简单实现:
import java.util.ArrayList;
import java.util.Arrays;
import java.util.HashMap;
import java.util.List;
public class AcAutomaton {
/**
* trie树的根节点
* */
private static TrieNode rootNode;
/**
* 添加词
* */
public static void addWord(String word) {
if (null == rootNode) {
rootNode = new TrieNode();
}
TrieNode currentNode = rootNode;
for (char c : word.toCharArray()) {
if (null == currentNode.getSubNodes()) {
currentNode.setSubNodes(new HashMap<>());
}
if (!currentNode.getSubNodes().containsKey(c)) {
TrieNode node = new TrieNode();
currentNode.getSubNodes().put(c, node);
}
currentNode = currentNode.getSubNodes().get(c);
}
currentNode.setWord(word);
}
/**
* 广度优先创建失败指针
* */
private static void bfsFailePointProcess(List nodes) {
if (nodes.isEmpty()) {
return;
}
List nextNodes = new ArrayList<>();
nodes.stream().forEach(node -> {
if (null != node.getSubNodes()) {
node.getSubNodes().forEach((k, v) -> {
nextNodes.add(v);
if (node.getFaileNode() == null) {
v.setFaileNode(node);
} else {
TrieNode currentNode = node;
while (currentNode.getFaileNode().getSubNodes() == null || !currentNode.getFaileNode().getSubNodes().containsKey(k)) {
currentNode = currentNode.getFaileNode();
if (null == currentNode.getFaileNode()) {
v.setFaileNode(currentNode);
break;
}
}
if (null == v.getFaileNode()) {
v.setFaileNode(currentNode.getFaileNode().getSubNodes().get(k));
}
}
});
}
});
bfsFailePointProcess(nextNodes);
}
/**
* 节点类
* */
static class TrieNode {
// 子结点
private HashMap subNodes;
// 失败指针
private TrieNode faileNode;
// 词条信息,若到此结点不是词则为null
private String word;
public HashMap getSubNodes() {
return subNodes;
}
public void setSubNodes(HashMap subNodes) {
this.subNodes = subNodes;
}
public TrieNode getFaileNode() {
return faileNode;
}
public void setFaileNode(TrieNode faileNode) {
this.faileNode = faileNode;
}
public String getWord() {
return word;
}
public void setWord(String word) {
this.word = word;
}
}
/**
* 匹配词
* */
public List matchWord(String sentence) {
List words = new ArrayList<>();
TrieNode currentNode = rootNode;
for (int i = 0; i < sentence.length(); i++) {
char c = sentence.charAt(i);
TrieNode nextNode = null;
while (null == currentNode.getSubNodes() || null == currentNode.getSubNodes().get(c)) {
if (currentNode.getFaileNode() == null) {
break;
}
currentNode = currentNode.getFaileNode();
if(null != currentNode.getWord())
words.add(currentNode.getWord());
}
if (null != currentNode.getSubNodes()) {
nextNode = currentNode.getSubNodes().get(c);
}
if (nextNode == null) {
continue;
}
if (null != nextNode.getWord()) {
words.add(nextNode.getWord());
}
currentNode = nextNode;
}
return words;
}
public static void main(String[] args){
AcAutomaton acAutomaton = new AcAutomaton();
Arrays.asList("大学","大学生","学习","学习机","学生","生气","生活","活着").forEach(word -> acAutomaton.addWord(word));
bfsFailePointProcess(Arrays.asList(rootNode));
String sentence = "大学生活";
acAutomaton.matchWord(sentence).forEach(System.out::println);
}
} 执行这段代码会输出:
大学
大学生
学生
生活在匹配到了词典中所有出现在句子中的词之后,继续第二步:在得到的集合中找到所有能组合成“大学生活”这个句子的子集。但是在这个地方遇到了一个小问题,上面查到的4个词中仅有“大学”和“生活”这两个词可以组成“大学生活”这个句子,而“大学生”和“生活”则无法在匹配到的词中找到能够与其连接的词汇。现实情况中,词典很难囊括所有词汇,所以这种情况时有发生。在这里,可以额外将单个字放到匹配到的词的集合中,这得到了一个新集合:
[大学、大学生、学生、生活]U[大、学、生、活] = [大学、大学生、学生、生活、大、学、生、活]
可以用一个有向图来表示这个集合的分词组合,从开始节点到结束节点的全部路径就是所有分词方式。
代码实现上,这种有向图可以使用邻接链表或者十字链表来存放。
那么在这些可能的分词组合中,应该选取哪一种作为最终的分词结果呢?大部分分词器的主要差异也体现在这里,有些分词器可能有很多不同的分词策略供使用者选择。例如最少词策略,就是在有向图中选择能够达到结束节点的全部路径中最短(经过最少节点)的一条。对于上面这张有向图,最短路径有两条,分别是“大学,生活”与“大学生,活”最终的分词结束就在这两条路径中选择一条。这种选择方法最为简单,性能也很高,但是准确性较差。其实仔细考虑一下不难发现,无论使用哪种分词策略,其目的都是想要挑选出一条最可能正确的,也就是概率最大的一种。“大学生活”分词为[大、学、活]的概率为P(大)P(学|大)P(生|大,学)P(活|大,学,生),这就是说,想要计算其的概率,需要知道“大”的出现概率,“大”出现时“学”出现的概率,“大”、“学”同时出现时“生”的概率,“大”,“学”,“生”同时出现时出现“活”的概率。这些出现概率可以在一份由大量文章组成的文本库中统计得出,但是问题是,如果词典要记录任意N个词出现时出现词W的概率,一个存放M个词汇的词典需要存放M^N量级的关系数据,这个词典会太大,所以通常会限制N的大小,一般来说,N为2或者为3,计算条件概率时只考虑到它前面2到3个词,这是基于马尔可夫链做的简化。当N为2时称为二元模型,N为3时称为三元模型。一个有50万词的词典的二元模型需要50万*50万条关系,这也是相当大的一个量级,可以对其进行压缩或转化为其它近似形式,这部分相对比较复杂,在此不作讲解,这里使用更简单一些的形式,假设每个词的出现都是独立事件,令P(大,学,生,活)=P(大)P(学)P(生)P(活)。要计算这个概率,只需要知道每个词的出现概率,一个词的出现概率=词出现的次数/文本库中词总量。那么将之前使用的词典更新为[大学5、大学生4、学习6、学习机3、学生5、生气8、生活7、活着2] 后面的数字是这些词在文本库中出现的次数,文本库中词的问题就是这些词出现次数之和=5+4+6+3+5+8+7+2=40
那么P(大学,生活)=P(大学)P(生活)=5/40*7/40
P(大学生、活)=P(大学生)P(活)=4/40*0/40 在这个地方出现了问题,对于词典里不存在的词,它的概率是0,这将会导致整个乘积是0,这是不合理的,对于这种情况可以做平滑处理,简单地来说,可以设词典中不存在的词的出现次数为1,于是P(大学生、活)=P(大学生)P(活)=4/40*1/40
最终可以挑选出一条最有可能的分词组合。至此第三步结束。
因为后续两步的代码相对复杂,代码不在此处贴出,感兴趣的可以参考我在git上分享的一份分词器代码。https://github.com/fuhongyuan/EasyTokenizer 初次发博文,水平有限,难免出现错误和讲述不清的地方,望各位理性指出共同进步。