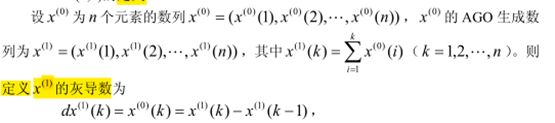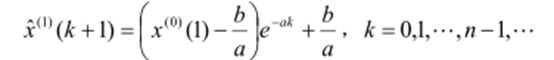【数学建模】数模day13-灰色系统理论I-灰色关联与GM(1,1)预测

接下来学习灰色系统理论。

0.

什么是灰色系统？

部分信息已知而部分信息未知的系统，我们称之为灰色系统。相应的，知道全部信息的叫白色系统，完全未知的叫黑色系统。

为什么采用灰色系统理论？

在给定信息不多，并且无法建立客观的物理原型，其作用原理亦不明确，内部因素难以辨识或之间关系隐蔽，人们很难准确了解这类系统的行为特征，因此对其定量描述难度较大。这时就采用“灰色系统理论”。

比如说，社会、经济、农业、生态问题的系统中，噪声普遍存在，一般受随机侵蚀的系统理论立足于【概率统计】，比如回归分析、方差分析、主成分分析等等。但是这些在小样本（数据不足）、样本没有较好的统计分布规律、难以量化等问题下，都不能够很好的胜任。尤其是，涉及到预测问题时，直接回归方程代入数得”预测“明显不符合客观规律，而使用灰色预测（通常使用GM(1,1)）更可靠。

1.

关联分析

这个方法解决的是：因素之间关联性如何，关联程度如何量化的问题。

讨论因素之间关联性如何，之前我们采用【回归分析】，即因变量对自变量求回归方程，这是基于更多样本的量化讨论。为了做【整体系统分析】，得到一个好的【直观过程】，以及为了【定性描述】，可以考虑采用【关联分析】。

实际上，实际应用中，我们可以【关联分析】+【回归分析】一起做。

关联分析实际上是动态过程发展态势的量化比较分析。

简而言之，关联分析是从整体态势上把握两（多）变量（每个变量的不同样本构成数列）之间的相关程度，并且从整体上分析减少了异常点的影响。
所谓发展态势比较，也就是系统各时期有关统计数据的几何关系的比较。

1) 做关联分析首先讨论数据变换技术。

通过数据变换消除【量纲】，使其具有【可比性】。

2) 做关联分析：

3) 关联分析案例：

分析求解：

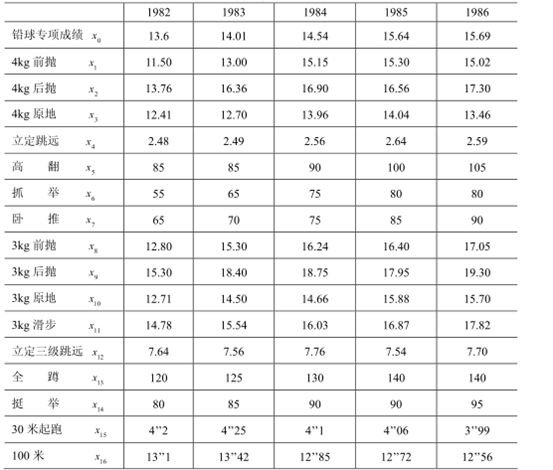
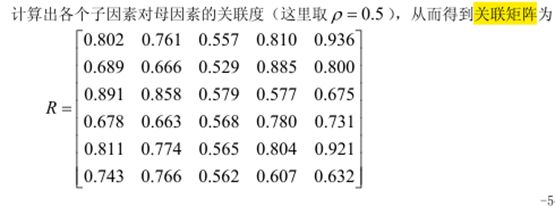
依照问题的要求，我们自然选取铅球运动员专项成绩作为参考数列，将其余的各个数列的初始化数列代入计算关联度公式，易算出各数列的关联度如下表：

关联度表：

matlab程序如下：

数据：x.txt

13.6  14.01  14.54  15.64  15.69
 11.50  13.00  15.15  15.30  15.02
 13.76  16.36  16.90  16.56  17.30
 12.41  12.70  13.96  14.04  13.46
 2.48  2.49  2.56  2.64  2.59
 85  85  90  100  105
 55  65  75  80  80
 65  70  75  85  90
 12.80  15.30  16.24  16.40  17.05
 15.30  18.40  18.75  17.95  19.30
 12.71  14.50  14.66  15.88  15.70
 14.78  15.54  16.03  16.87  17.82
 7.64  7.56  7.76  7.54  7.70
 120  125  130  140  140
 80  85  90  90  95
 4.2  4.25  4.1  4.06  3.99
 13.1  13.42  12.85  12.72  12.56

程序：

 1 % 关联分析
 2 load x.txt
 3  for i = 1:15
 4      x(i,:) = x(i,:)/x(i,1); %前15数列做标准化
 5 end
 6  for i = 16:17
 7      x(i,:) = x(i,1)./x(i,:); %后两个做标准化
 8 end
 9  data = x;
10  n = size(data,2); %矩阵列数，即观测时刻的个数
11 ck = data(1,:); %选第一列是参考数列
12 bj = data(2:end,:);%其余列是比较数列
13 m2 = size(bj,1);%比较数列个数
14 for j = 1:m2
15      t(j,:) = bj(j,:)-ck;
16  end
17  mn = min(min(abs(t'))); %最小差
18 mx = max(max(abs(t'))); %最大差
19 rho = 0.5; %分辨系数设置
20 ksi = (mn + rho*mx)./(abs(t)+rho*mx);%求关联系数
21 r = sum(ksi')/n %关联度
22 [rs,rind] = sort(r,'descend') %关联度排序‘

matlab结果：

依次打印关联度：

r =

  1 至 6 列

    0.5881    0.6627    0.8536    0.7763    0.8549    0.5022

  7 至 12 列

    0.6592    0.5820    0.6831    0.6958    0.8955    0.7047

  13 至 16 列

    0.9334    0.8467    0.7454    0.7261

排序后：

rs =

  1 至 6 列

    0.9334    0.8955    0.8549    0.8536    0.8467    0.7763

  7 至 12 列

    0.7454    0.7261    0.7047    0.6958    0.6831    0.6627

  13 至 16 列

    0.6592    0.5881    0.5820    0.5022

rind =

  1 至 10 列

    13    11     5     3    14     4    15    16    12    10

  11 至 16 列

     9     2     7     1     8     6

2.

优势分析：

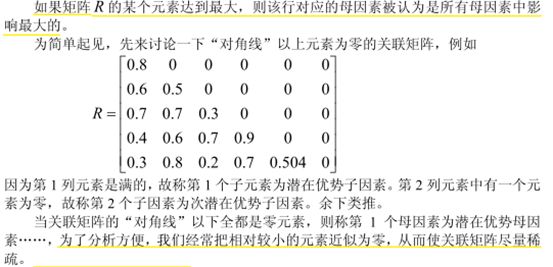
一个例子：假如有关联度矩阵如下：

分析：

3.

生成数：

我们主要使用【累加生成】，其理论如下：

应用中，最常用的是 1 次累加生成。
一般地，经济数列等实际问题的数列皆是非负数列，累加生成可使非负的摆动与非摆动的数列或任意无规律性的数列转化为非减的数列。

有些实际问题的数列中有负数（例如温度等），累加时略微复杂。有时，由于出现正负抵消这种信息损失的现象，数列经过累加生成后规律性非但没得到加强，甚至可能被削弱。对于这种情形，我们可以先进行【移轴】，然后再做【累加生成】。

4.

灰色GM(1,1)模型

GM是Grey Model的简写。

1）GM(1,1)定义：

2）GM(1,1)的白化型：

应当注意,GM(1,1)表示模型师一阶方程并且只有一个变量；推广之，加入有m个方程，n个变量则为G(m,n)。pdf讨论了G(1,N)/G(2,N)等，用到再说，对于这里，我们首先详细使用G(1,1)。

5.

灰色预测

灰色预测是指利用 GM 模型对系统行为特征的发展变化规律进行估计【预测】，同时也可以对行为特征的异常情况发生的时刻进行估计计算(把异常时间作为数列)，以及对在特定时区内发生事件的未来时间分布情况做出研究等等。这些工作实质上是将“随机过程”当作“灰色过程”，“随机变量”当作“灰变量”，并主要以灰色系统理论中的 【GM(1,1)模型】来进行处理。

1) 灰色预测的方法

2) 灰色预测处理的步骤(使用)

1. 数据的检验和处理

2. 建立模型

参考上述GM(1,1)方法，建立GM(1,1)模型，并求解该微分方程，得到预测值：

3. 检验预测值

4. 预测预报

由模型 GM(1,1)所得到的指定时区内的预测值，根据实际问题的需要，给出相应的
预测预报。

另一个应用--灾变预测

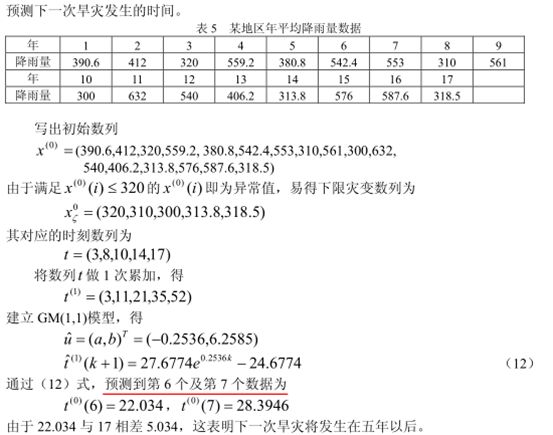
一个案例：

假定小于320为异常。预测下一次异常出现的时间(旱灾)。

6.

灰色预测计算实例：如何使用、求解以及分析

灰色G(1,1)预测步骤：

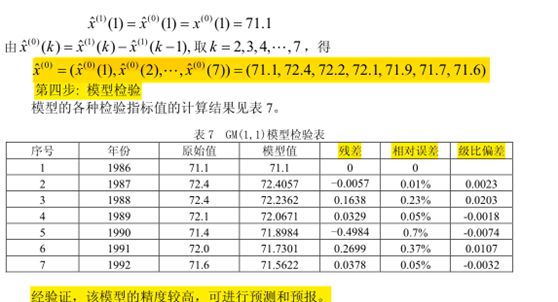
步骤： 第一步：级比检验 (1)求级比，列出级比向量。 (2)级比判断：若所有级比都落在可容覆盖内，则通过，说明原始数据适合使用GM(1,1)   第二步：GM(1,1)建模 （1）原始数据做一次累加 （2）列出GM(1,1)模型 第三步：求解模型 （1）最小二乘法求解GM(1,1) （2）求生成数列预测值以及模型还原值 （3）相应可以得到预测值-真实值比较表格 第四步：模型检验 （1）原始值-模型值-残差-相对误差0级比偏差表格 （2）根据表格作出说明

一个实例：

北方某城市 1986～1992 年道路交通噪声平均声级数据如下：

                                    

序号	年份	Leq
1	1986	71.1
2	1987	72.4
3	1988	72.4
4	1989	72.1
5	1990	71.4
6	1991	72.0
7	1992	71.6

求解分析：

求解MATLAB程序如下：

%此程序原著pdf上程序是有bug的，以下已经调通

 1 clc,clear
 2  x0=[71.1 72.4 72.4 72.1 71.4 72.0 71.6]';%注意这里为列向量
 3 n=length(x0);
 4  lamda=x0(1:n-1)./x0(2:n) %计算级比
 5 range=minmax(lamda') %计算级比的范围
 6 x1=cumsum(x0); %累加运算
 7 B=[-0.5*(x1(1:n-1)+x1(2:n)),ones(n-1,1)];
 8  Y=x0(2:n);
 9  u=B\Y %最小二乘，拟合参数
10 syms x(t)
11  x=dsolve(diff(x)+u(1)*x==u(2),x(0)==x0(1));
12  x=subs(x,{'a','b','x0'},{u(1),u(2),x1(1)});
13  yuce1=subs(x,t,[0:n-1]);
14  yuce1 = double(yuce1);
15  %为提高预测精度，先计算预测值，再显示微分方程的解
16 y=vpa(x,6) %其中的 6 表示显示 6 位数字
17 yuce=[x0(1),diff(yuce1)] %差分运算，还原数据
18 epsilon=x0'-yuce %计算残差
19 delta=abs(epsilon./x0') %计算相对误差
20 rho=1-(1-0.5*u(1))/(1+0.5*u(1))*lamda' %计算级比偏差值

求解结果如下：

级比：

lamda =

    0.9820
     1.0000
     1.0042
     1.0098
     0.9917
     1.0056

级比范围：
range =

    0.9820    1.0098

模型参数：
u =

    0.0023
    72.6573

求解模型得方程：
y = 31000.0 - 30928.9*exp(-0.00234379*t)
 

模型值：

yuce =

  1 至 6 列

   71.1000   72.4057   72.2362   72.0671   71.8984   71.7301

  7 列

   71.5622

残差：
epsilon =

  1 至 6 列

         0   -0.0057    0.1638    0.0329   -0.4984    0.2699

  7 列

    0.0378

相对误差：
delta =

  1 至 6 列

         0    0.0001    0.0023    0.0005    0.0070    0.0037

  7 列

    0.0005

级比偏差：
rho =

    0.0203    0.0023   -0.0018   -0.0074    0.0107   -0.0032

转载于:https://www.cnblogs.com/duye/p/9400503.html