降噪自动编码器（Denoising Autoencoder)

起源：PCA、特征提取....

随着一些奇怪的高维数据出现，比如图像、语音，传统的统计学-机器学习方法遇到了前所未有的挑战。

数据维度过高，数据单调,噪声分布广，传统方法的“数值游戏”很难奏效。数据挖掘？已然挖不出有用的东西。

为了解决高维度的问题，出现的线性学习的PCA降维方法，PCA的数学理论确实无懈可击，但是却只对线性数据效果比较好。

于是，寻求简单的、自动的、智能的特征提取方法仍然是机器学习的研究重点。比如LeCun在1998年CNN总结性论文中就概括了今后机器学习模型的基本架构。

 

当然CNN另辟蹊径，利用卷积、降采样两大手段从信号数据的特点上很好的提取出了特征。对于一般非信号数据，该怎么办呢？？

 

Part I  自动编码器（AutoEncoder）

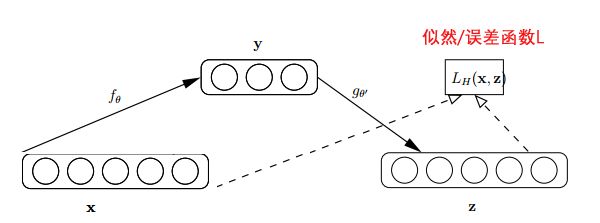
自动编码器基于这样一个事实：原始input（设为x）经过加权（W、b)、映射（Sigmoid）之后得到y，再对y反向加权映射回来成为z。

通过反复迭代训练两组（W、b），使得误差函数最小，即尽可能保证z近似于x，即完美重构了x。

那么可以说正向第一组权（W、b）是成功的，很好的学习了input中的关键特征，不然也不会重构得如此完美。结构图如下：

 

从生物的大脑角度考虑，可以这么理解，学习和重构就好像编码和解码一样。

 

这个过程很有趣，首先，它没有使用数据标签来计算误差update参数，所以是无监督学习。

其次，利用类似神经网络的双隐层的方式，简单粗暴地提取了样本的特征。 

这个双隐层是有争议的，最初的编码器确实使用了两组（W，b），但是Vincent在2010年的论文中做了研究，发现只要单组W就可以了。

即W'=W^T, W和W’称为Tied Weights。实验证明，W'真的只是在打酱油，完全没有必要去做训练。

逆向重构矩阵让人想起了逆矩阵，若W^-1=W^T的话，W就是个正交矩阵了，即W是可以训成近似正交阵的。

由于W'就是个酱油，训练完之后就没它事了。正向传播用W即可，相当于为input预先编个码，再导入到下一layer去。所以叫自动编码器，而不叫自动编码解码器。

 

 

Part II 降噪自动编码器（Denoising Autoencoder）

Vincent在2008年的论文中提出了AutoEncoder的改良版——dA。推荐首先去看这篇paper。

论文的标题叫 "Extracting and Composing Robust Features"，译成中文就是"提取、编码出具有鲁棒性的特征"

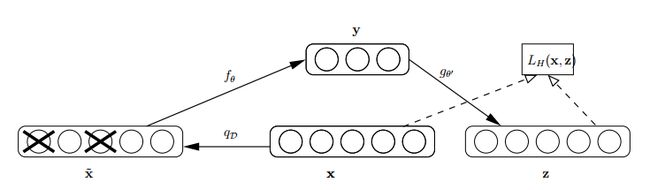
怎么才能使特征很鲁棒呢？就是以一定概率分布（通常使用二项分布）去擦除原始input矩阵，即每个值都随机置0,  这样看起来部分数据的部分特征是丢失了。

以这丢失的数据x'去计算y，计算z，并将z与原始x做误差迭代，这样，网络就学习了这个破损（原文叫Corruputed）的数据。

这个破损的数据是很有用的，原因有二：

其之一，通过与非破损数据训练的对比，破损数据训练出来的Weight噪声比较小。降噪因此得名。

原因不难理解，因为擦除的时候不小心把输入噪声给×掉了。

其之二，破损数据一定程度上减轻了训练数据与测试数据的代沟。由于数据的部分被×掉了，因而这破损数据

一定程度上比较接近测试数据。（训练、测试肯定有同有异，当然我们要求同舍异）。

这样训练出来的Weight的鲁棒性就提高了。图示如下：

关键是，这样胡乱擦除原始input真的很科学？真的没问题？  Vincent又从大脑认知角度给了解释：

paper中这么说到：人类具有认知被阻挡的破损图像能力，此源于我们高等的联想记忆感受机能。

我们能以多种形式去记忆（比如图像、声音，甚至如上图的词根记忆法），所以即便是数据破损丢失，我们也能回想起来。

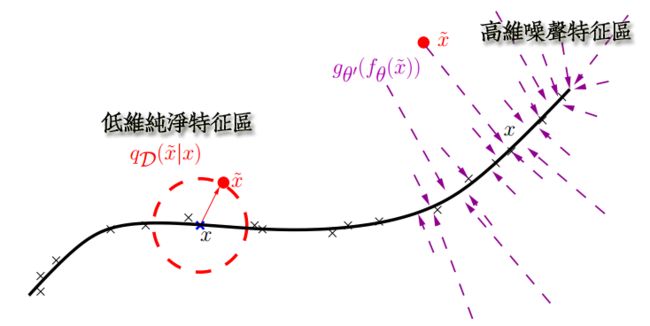
另外，就是从特征提取的流形学习(Manifold Learning)角度看：

破损的数据相当于一个简化的PCA，把特征做一个简单的降维预提取。

 

Part III  自动编码器的奇怪用法

自动编码器相当于创建了一个隐层，一个简单想法就是加在深度网络的开头，作为原始信号的初级filter，起到降维、提取特征的效果。

关于自动编码器取代PCA的基本用法，参考 http://www.360doc.com/content/15/0324/08/20625606_457576675.shtml

当然Bengio在2007年论文中仿照DBN较之于RBM做法：作为深度网络中各个layer的参数初始化值，而不是用随机小值。

即变成了Stacked AutoEncoder。

当然，这种做法就有一个问题，AutoEncoder可以看作是PCA的非线性补丁加强版，PCA的取得的效果是建立在降维基础上的。

仔细想想CNN这种结构，随着layer的推进，每层的神经元个数在递增，如果用了AutoEncoder去预训练，岂不是增维了？真的没问题？

paper中给出的实验结果认为AutoEncoder的增维效果还不赖，原因可能是非线性网络能力很强，尽管神经元个数增多，但是每个神经元的效果在衰减。

同时，随机梯度算法给了后续监督学习一个良好的开端。整体上，增维是利大于弊的。

 

Part IV  代码与实现

具体参考  http://deeplearning.net/tutorial/dA.html

有几个注意点说下：

①cost函数可以使用交错熵(Cross Entroy)设计，对于定义域在[0,1]这类的数据，交错熵可用来设计cost函数。

其中Logistic回归的似然函数求导结果可看作是交错熵的特例。参考 http://en.wikipedia.org/wiki/Cross_entropy

也可以使用最小二乘法设计。

②RandomStreams函数存在多个，因为要与非Tensor量相乘，必须用shared版本。

所以是  from theano.tensor.shared_randomstreams import RandomStreams

而不是 from theano.tensor import RandomStreams