python时间序列（ARIMA）分析步骤

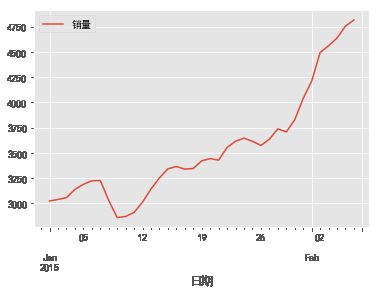
data = pd.read_excel(r'C:\Users\Administrator\Desktop\arima_data.xls',index_col = '日期')

data.plot()

单调递增的，不平稳

单位根检验下

from statsmodels.tsa.stattools import adfuller as ADF

ADF(data['销量'])

>>>
(1.8137710150945274,
 0.9983759421514264,
 10,
 26,
 {'1%': -3.7112123008648155,
  '10%': -2.6300945562130176,
  '5%': -2.981246804733728},
 299.46989866024177)

元组第二个值为p值，p>0.05，接受原假设，存在单位根

 

差分（1阶）

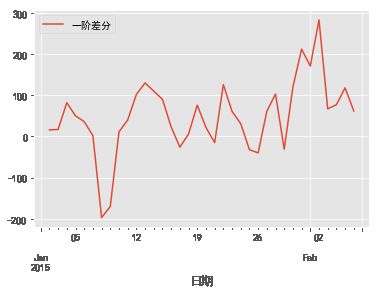
d_data = data.diff().dropna()
d_data.columns = ['一阶差分']
d_data.plot()

再次单位根检验下

ADF(d_data['一阶差分'])

>>>
(-3.1560562366723532,
 0.02267343544004886,
 0,
 35,
 {'1%': -3.6327426647230316,
  '10%': -2.6130173469387756,
  '5%': -2.9485102040816327},
 287.5909090780334)

p<0.05,拒绝原假设，不存在单位根了。

随机性检验（白噪声检验）

from statsmodels.stats.diagnostic import acorr_ljungbox

acorr_ljungbox(d_data,lags =1)

>>>
(array([11.30402222]), array([0.00077339]))

p=0.00077339<0.05，拒绝原假设，所以一阶差分后的序列不是随机的。

确定阶数p,q建模

一、根据自相关系数和偏自相关系数目测

模型	自相关系数（ACF）	偏自相关系数（PACF）
AR（P）	拖尾	p阶截尾
MA（q）	q阶截尾	拖尾
ARMA（p，q）	p阶拖尾	q阶拖尾

p看pacf，q看acf

from statsmodels.graphics.tsaplots import plot_acf
from statsmodels.graphics.tsaplots import plot_pacf

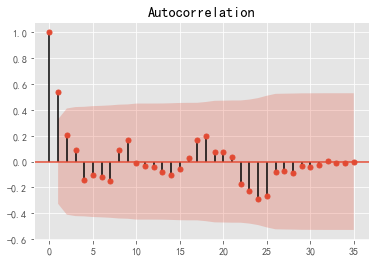
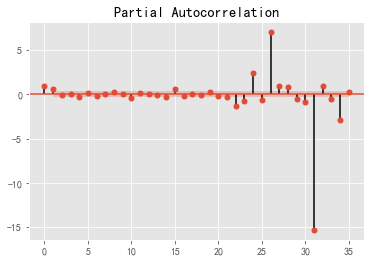
plot_acf(d_data)
plot_pacf(d_data)

由上图可知，p = 0，q=1

二、根据bic遍历p，q值，取bic最小时对应的p，q

from statsmodels.tsa.arima_model import ARIMA

tmp = []
for p in range(4):
    for q in range(4):
        try:
            tmp.append([ARIMA(data,(p,1,q)).fit().bic,p,q])
        except:
            tmp.append([None,p,q])

tmp = pd.DataFrame(tmp,columns = ['bic','p','q'])
tmp[tmp['bic'] ==tmp['bic'].min()]

>>>
	   bic     	p	q
	422.510082	0	1

与目测一样，综上p = 0，q = 1

 

建模预测

model = ARIMA(data,(0,1,1)).fit()
model.summary()

>>>
ARIMA Model Results
Dep. Variable:	D.销量	No. Observations:	36
Model:	ARIMA(0, 1, 1)	Log Likelihood	-205.880
Method:	css-mle	S.D. of innovations	73.086
Date:	Tue, 31 Jul 2018	AIC	417.760
Time:	15:12:13	BIC	422.510
Sample:	01-02-2015	HQIC	419.418
- 02-06-2015		
coef	std err	z	P>|z|	[0.025	0.975]
const	49.9561	20.139	2.481	0.018	10.484	89.428
ma.L1.D.销量	0.6710	0.165	4.071	0.000	0.348	0.994
Roots
Real	Imaginary	Modulus	Frequency
MA.1	-1.4902	+0.0000j	1.4902	0.5000


yp = model.forecast(5)#预测未来5年
yp[0]
>>>
array([4873.9665477 , 4923.92261622, 4973.87868474, 5023.83475326,
       5073.79082178])

完！