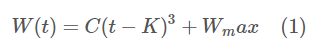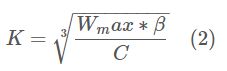CUBIC拥塞拥塞控制算法

背景和意义

随着Internet的发展，网络中出现了越来越多的高速和长距离链路，这些链路的特点是时延带宽积（BDP=bandwith*RTT）很大，也就是说，这些链路所能容纳的总数据量很大。

传统TCP协议，例如TCP-Reno、TCP-NewReno、TCP-SACK中，每过一个RTT（Round Trip Times），窗口增加一个单位，这使得TCP的数据传输速度缓慢，远不能充分利用网络带宽。当碰上高带宽环境时，可能需要经历很多个RTT，拥塞窗口才能接近于一个BDP。如果数据流很短，可能拥塞窗口还没增长到一个BDP，数据流就已经结束了，这种情况的带宽利用率就会非常低。

假设网络带宽是10Gbps，RTT是100ms，数据包是固定的1250字节，则此网络所能容纳的数据包总量是：\(\dfrac{10\times 10^9\times 0.1}{1250\times 8}=10^5\)个数据包。假设窗口从50000开始增长，也需要50000个RTT（1.4个小时）才能达到网路的满负荷，如果一个TCP流在此之前结束（显然往往如此），则未充分利用带宽。

BIC-TCP

BIC-TCP采用二分搜索的方式来决定拥塞窗口的增长尺度，首先它会记录拥塞窗口的一个最大值点，这个最大值就是TCP最近一次出现丢包时拥塞窗口的值；还会记录一个最小值点，即在一个RTT周期内没有出现丢包事件时窗口的大小。二分搜索就是取最小值和最大值的中间点，当拥塞窗口增长到这个中间值且没有出现丢包的话，就说明网络还可以容纳更多的数据包。那么将这个中值设为新的最小值，在新的最小值和最大值间搜索中间值。当前拥塞窗口的值还远没有达到通道的容量时，其增长速度很快；相反，当拥塞窗口的值接近于通道的容量时，其拥塞窗口增长函数是一个简化的对数凸函数。这个凸函数使拥塞窗口在饱和点或平衡点比凹函数或线性函数保持更长的时间，在饱和点处，凸函数和线性函数具有最大的窗口增量，因此在丢包发生时会出现大量的数据包被丢失。

BIC-TCP的主要特征是在前面说过的其独特的窗口增长函数，图1给出了BIC-TCP的窗口增长函数。当出现丢包事件时，BIC-TCP通过乘以因子 \(\beta\) 来缩小窗口，缩小之前的窗口大小被设置为最大值\(W_{\max}\) ，并且缩小之后的窗口大小被设置为最小值\(W_{\min}\) 。 然后，BIC-TCP使用这两个参数执行二分搜索，拥塞窗口的下一个取值会是\(W_{\max}\) 和\(W_{\min}\) 之间的“中点” \(W_{mid}\) 。

为了防止拥塞窗口从\(W_{\min}\) 增长到 \(W_{\max}\) 的步长step太大，BIC-TCP还设置了一个常数\(S_{\max}\) ，当step>\(S_{\max}\) 时，BIC-TCP会取下一个增长点为 \(W_{\min}\)+\(S_{\max}\) 而不是 \(W_{mid}\) （加法增加阶段），如果没有出现丢包的话，再更新\(W_{\min}\) ，直到step< \(S_{\max}\) 为止。与此同时BIC-TCP还设置一个另一个控制参数\(S_{\min}\) ，当窗口增量小于 \(S_{\min}\) 时，BIC-TCP会将当前拥塞窗口值设为最大值。

如果窗口增长超过最大值，则说明当前窗口最大值还不是一个饱和点，网络还可以容纳更多的数据包，窗口还有增长的空间，一个新的窗口最大值需要被探索。于是BIC-TCP会进入一个新的阶段，叫做最大值探索阶段。最大探测使用一个与在加法增长和二分搜索阶段完全对称的窗口增长函数。图1中给出了在最大探索阶段期间的窗口增长函数。在最大探测期间，窗口最初缓慢地增长以发现附近新的最大值，经过一段时间的缓慢增长，如果没有找到新的最大值（即没出现包丢失），则它猜测新的最大值离得很远，所以它给窗口大小增加一个大的固定增量，使用加法增加切换到更快的增加速度。BIC-TCP的良好性能来自 \(W_{\max}\) 附近的缓慢增加以及在加法增加和最大探测期间的线性增加。

BIC-TCP在高速网络中具有良好的可扩展性、多个流竞争的公平性和低窗口振荡的稳定性。然而，BIC-TCP的增长功能对于TCP来说仍然过于激进，特别是在短RTT或低速网络下。此外，窗口控制的几个不同阶段（二进制搜索增加、最大探测、\(S_{\max}\) 和 \(S_{\min}\) ）增加了协议实现和性能分析的复杂性。

算法与推导

算法简述

CUBIC是BIC-TCP的下一代版本。 它通过用三次函数（包含凹和凸部分）代替BIC-TCP的凹凸窗口生长部分，大大简化了BIC-TCP的窗口调整算法, 该函数在保留BIC-TCP的优点（特别是其稳定性和可扩展性）的同时，简化了窗口控制，增强了其TCP友好性。实际上，任何奇数阶多项式函数都具有这种形状。三次函数的选择是偶然的，但是也是出于方便。CUBIC的关键特征是其窗口增长仅取决于两个连续拥塞事件之间的时间。一个拥塞事件是指出现TCP快速恢复的时间。因此，窗口增长与RTT无关。 这个特性允许CUBIC流在同一个瓶颈中竞争，有相同的窗口大小，而不依赖于它们的RTT，从而获得良好的RTT公平性。而且，当RTT较短时，由于窗口增长率是固定的，其增长速度可能比TCP标准慢。 由于TCP标准（例如，TCP-SACK）在短RTT下工作良好，因此该特征增强了协议的TCP友好性。

CUBIC窗口增长函数

CUBIC的窗口增长函数是一个三次函数，非常类似于BIC-TCP的窗口增长函数，CUBIC的函数图像如图2所示。CUBIC的详细运行过程如下，当出现丢包事件时，CUBIC同BIC-TCP一样，会记录这时的拥塞窗口大小作为\(W_{\max}\)，接着通过常数因子\(\beta\) 执行拥塞窗口的乘法减小，这里 \(\beta\) 是一个窗口降低常数，并进行正常的TCP快速恢复和重传。从快速恢复阶段进入拥塞避免后，使用三次函数的凸函数增加窗口。三次函数设置在 \(W_{\max}\) 处达到稳定点，如果存在新的最大窗口（网络带宽发生变化）, 然后使用三次函数的凹函数开始探索新的最大窗口。

CUBIC的窗口增长函数公式如下所示：

\(C\)是一个CUBIC的参数， \(t\)是从窗口上次降低开始到现在的时间，是一个弹性值，而 \(K\) 是上述函数在没有进一步丢包的情况下将当前的拥塞窗口 \(W\) 增加到 \(W_{\max}\) 经历的时间。

\(K\)计算公式如下：

在拥塞避免阶段每收到一个ACK，CUBIC都会使用方程（1）计算在下个RTT的窗口增长速率。CUBIC使用$W\left( t+RTT \right) $作为拥塞窗口的候选值，假设当前拥塞窗口大小为 \(cwnd\)。根据 \(cwnd\)的值，CUBIC有三种运行模式。在linux内核实现中，\(K\)值立方根求取使用得是牛顿迭代法，这是因为牛顿迭代法的性能优于二分法。

如果\(cwnd\) 小于（标准）TCP在上次丢包事件之后 \(t\) 时刻到达的窗口大小，那么CUBIC处于TCP模式（我们将在下面描述如何根据时间确定标准TCP的窗口大小）。

如果\(cwnd\) 小于\(W_{\max}\) ，那么CUBIC在三次函数的凸函数区域。

如果\(cwnd\) 大于\(W_{\max}\) ，那么CUBIC处于三次函数的凹区域。

TCP友好型区域

标准TCP协议在网络时延带宽积小或者RTT小的情况下表现仍不错，CUBIC被设计为在这两种情况下可以很好的兼容标准TCP协议。算法执行过程中，每收到一个ACK后都会判断当前是否处于标准TCP阶段，即TCP友好域，以此来更好的兼容TCP。因此需要通过TCP的AIMD（加法增、乘法减）特性并使用加法因子 $\alpha $ 和乘法因子 \(\beta\) 去估算在TCP传统拥塞算法下的拥塞窗口大小。

\(W_{\max}\left( 1-\beta \right)\)是当发生拥塞事件时减少后的初始 \(cwnd\)， \(3\frac{\beta}{2-\beta}\)为线性增长的大小(斜率)， \(\frac{t}{RTT}\)为从发生拥塞窗口到至今需要经历RTT的个数。如果当前的 \(cwnd\) 小于\(W_{tcp\left( t \right)}\) ，则处于TCP模式，因此每次接受ACK时，都会将 \(cwnd\)设置为\(W_{tcp\left( t \right)}\) 。

凸区域

当在拥塞避免阶段收到一个ACK，如果协议不处于TCP模式，且\(cwnd\)小于\(W_{\max}\)，那么协议就处于凸区域，在这个区域，\(cwnd\) 的增量为：

凹区域

当前的\(cwnd\) 大于\(W_{\max}\) 时，协议就会进入凹区域。由于 \(cwnd\)大于先前的饱和点\(W_{\max}\) ，这表明自上次拥塞事件以来，网络条件可能受到干扰，这可能意味着在一些竞争流离开后，可用带宽会增加。由于网络是高度异步的，可用带宽的波动总是存在的。凹区域使得窗口在开始时增长非常缓慢，并逐渐增加其增长率。由于CUBIC正在搜索一个新的\(W_{\max}\) ，我们也将此阶段称为最大探测阶段。由于没有修改凹区域的窗口增长函数，因此两个区域的窗口增长函数保持不变。因此 \(cwnd\)的增量同样为：

乘法降低

当出现数据包丢失时，CUBIC会通过乘法因子 $\beta $ 来降低拥塞窗口，这里取\(\beta =0.2\) 。虽然自适应性的设置 $\beta $ 会导致更快的收敛，但是会使协议的分析变得更加困难，并影响协议的稳定性。

快速收敛机制

新的流量加入网络时，网络中的现有流量需要放弃其部分带宽份额，以使新流量有一定的增长空间。在发生丢包前，CUBIC会记录一个最大窗口值\(W_{\max}\) 。当发生丢包后，在降低窗口前，CUBIC又会记录当前的窗口值作为新的\(W_{\max}\) ，为了不至于混淆，可以将之前记录的\(W_{\max}\) 记为$ W_{last_max}\(。当发生丢包时，CUBIC会比较\) W_{last_max}$ 和\(W_{\max}\) 的大小，如果\(W_{\max}\) 小于$ W_{last_max}$ ，这表明由于可用带宽的变化，该流的窗口饱和点正在降低。这种情况下，CUBIC的做法是通过进一步的减小\(W_{\max}\) 来释放更多的可用带宽，使得新加入的流量有一定的增长空间。

伪码示例

对所需要的参数进行初始化，其中tcp_friendliness决定TCP友好型区域是否开启，默认为开启状态；fast_convergence决定快速收敛机制是否开启，默认为开启状态；其余的参数值需要放入cubic_reset()函数中，因为这些参数在每次发生拥塞时间后，都需要进行重置。其中 \(W_{last\_max}\) 为上一次发生拥塞窗口时所记录的窗口值；epoch_start会记录每次发生拥塞的时间；origin_point则记录\(W_{last\_max}\) 和当前的 \(cwnd\) 之间的最大值；dMin记录最小的RTT（往返传输时间）； \(W_{tcp}\)为TCP模式时的计算得出的窗口值； \(K\)是在没有进一步丢包的情况下将当前的拥塞窗口 \(W\)增加到\(W_{\max}\) 经历的时间；ack_cnt 记录接收到ACK的数量。

每当接受到一个ACK时，dMin会去记录自身与当前RTT的最小值，保证dMin记录着最小的RTT，这样做的原因是由于网络的不确定性因素，导致每个ACK对应的RTT可能也会有增加，因此需要找到最接近实际的RTT。ssthresh判断当前状态为慢启动还是拥塞避免阶段的阈值，如果当前的cwnd小于或等于ssthresh，那么进入慢启动阶段，每接收到一个ACK，cwnd相应自加一，直到cwnd大于ssthresh，则需要进入拥塞避免阶段，cubic_update()函数会计算得出一个cnt值，与cwnd_cnt进行比较，以此判断cwnd是否需要增长。

当包丢失（拥塞事件）时，通过快速恢复阶段，接下来就会重新进入拥塞避免。因此epoch_start需要置为0。如果发生拥塞事件时的cwnd小于上一次发生拥塞事件的\(W_{last\_max}\) ，并且快速收敛机制为开启状态，即意味着是由于新流的加入，导致cwnd小于\(W_{last\_max}\) ，因此需要将当前的cwnd需要让出一部分带宽给新流；否则就是由于网络的波动（带宽减少或增加）导致cwnd小于或大于\(W_{last\_max}\) ，那么只需要将当前的cwnd记录到\(W_{last\_max}\) 即可。当cwnd和ssthresh进行乘法减少后，重新开始拥塞避免阶段（即凸函数区域）

Cubic_update()函数为核心算法的实现。当epoch_start为零时，意味着重新进入拥塞避免后阶段，如果cwnd小于\(W_{last\_max}\)，需要计算cwnd到达\(W_{last\_max}\) 的时间K；反之如果cwnd大于\(W_{last\_max}\) ，意味着网络的带宽增加了，需要进行窗口最大值探索(凹函数区域)。时间\(t\)记录的是以拥塞避免阶段为起点时间到当前的时间之差，而后与dMin之和，因而去计算出下一个dMin所需要到达的目标窗口值target。如果target大于当前窗口值cwnd，需要增加窗口的增长率；反之，意味着当前窗口值已经到达平稳期，需要去降低窗口的增长率。

同时，也需要计算如果是在传统的TCP拥塞控制算法下的窗口值\(W_{tcp}\) ，然后\(W_{tcp}\) 与在CUBIC拥塞控制算法下的cwnd进行比较，以此判断是否进入tcp友好型区域。这样通过与TCP传统拥塞控制算法的组合，能够得到更高的网络质量。

总体流程

原理推导

CUBIC窗口增长函数的推导

从作者的角度来看，是如何从通过改进BIC算法得到CUBIC算法，最主要的还是窗口增长函数的变化。

从上图，可以看出该函数的斜率是从高到低，而后又慢慢增大。因此，可以直观假设其导数为二次曲线函数，以\(g\left( x \right) =3x^2-2x\)为例，它的图像如下图所示。

由此，可以得到它的原函数为\(f\left( x \right) =x^3-x^2+1\) ，即它的图像为

以上仅仅是个例子，目的在于确定CUBIC的曲线形状，上面的图像和BIC的窗口探测曲线很像，在确定了曲线的形状之后，最终要确定曲线的参数，而曲线的通用方程应该是：

\[f\left( x \right) =ax^3+bx^2+cx+d \]

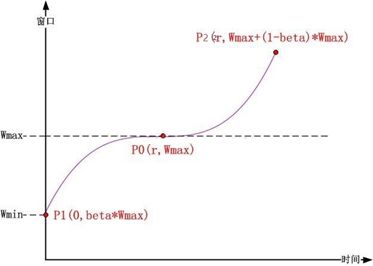
对于参数的确定，需要联系CUBIC拥塞控制算法的过程，\(W_{\min}\)实际上就是上次拥塞事件发生后最大窗口（ \(W_{\max}\) 记录着拥塞事件发生时所测量出的对应的最大窗口值，即为已知）乘法减少后的值，因此 \(W_{\min}=W_{\max}\times beta\)，再者由于函数的对称特性，能够计算得出最高点值为$W_{\max}+W_{\max}\left( 1-beta \right) $ 。

因此，可以得出以下的图像，由于这个函数增长图像对应着一次拥塞避免状态的重新开始，因此P1点处的时间为零，而由P1到P0的时间假设为r已知，根据对称的特性，因而P2处的时间也为2r。

由于曲线本身是关于P0(x=r, y=\(W_{\max}\) )这个点对称的，因此可以确定曲线方程的常数因子为\(W_{\max}\) ，所以能够将曲线方程写成如下的形式：

\[f\left( x \right) =h\left( x \right) +W_{\max}\ \ \ \ \ \ \left( 0 \right) \]

现在的目标就是求h(x)，再由于P1和P2点已知：

\[f\left( 0 \right) =\beta W_{\max}\ \ \ \ \left( 1 \right) \]

\[f\left( 2r \right) =2W_{\max}-\beta W_{\max}\ \ \ \ \ \left( 2 \right) \]

\[f\left( r \right) =W_{\max}\ \ \ \ \ \left( 3 \right) \]

由0、1、3式可得：

\[h\left( r \right) =0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \left( 4 \right) \]

\[h\left( 0 \right) =\left( \beta -1 \right) W_{\max}\ \ \ \ \ \ \ \left( 5 \right) \ \ \]

根据4式以及f(x) ,即h(x)为三次函数的特性，可以假设：

\[h\left( x \right) =C\left( x-K \right) ^3\ \ \ \ \ \ \left( 6 \right) \]

其中C为一常量，因此我们需要将5式代入6式中，可得：

\[K=\sqrt[3]{\frac{\left( 1-\beta \right) W_{\max}}{C}}\ \ \ \ \ \ \ \left( 7 \right) \]

综上可得：

\[f\left( x \right) =h\left( x \right) +W_{\max}=C\left( x-K \right) ^3+W_{\max}=C\left( x-\sqrt[3]{\frac{\left( 1-\beta \right) W_{\max}}{C}} \right) ^3+W_{\max} \]

TCP友好型区域\(W_{\max}\)窗口值公式的推导

上图为在TCP传统拥塞控制算法(New-Reno)下，窗口值随时间的变化过程，其中W对应着发生拥塞事件时的窗口值（最大窗口值），由于上图具有周期性，因此只需对第一个周期的图像进行分析即可，在发生拥塞事件后，需要对\(W\)进行乘法减少，即\(\left( 1-b \right) W\)(起点)，而后通过TCP的累计确认机制以固定的速率a去进行窗口值的增长，直到到达W。

显然，通过等差数列公式，可以得出：

\[\left( 1-b \right) W+na=W\ \ \ \ \ \ \ \left( 1 \right) \]

\[n=\frac{bW}{a}\ \ \ \ \ \ \ \ \ \ \ \ \ \left( 2 \right) \]

又该等差数列应该从零开始，所以

\[n=\frac{bW}{a}+1\ \ \ \ \ \ \ \ \left( 3 \right) \]

\(\left( 1-b \right) W\)需要n次RTT才能到达\(W\) ，因此在这一个周期内的平均窗口值\(S\)，应该拿窗口值总和，除以迭代增长的次数\(n\)。

\[S=\frac{n\left[ \left( 1-b \right) W+W \right]}{2n}=\frac{2-b}{2}W\ \ \ \ \ \ \ \left( 4 \right) \]

假设RTT为R时间（second），因此每秒的发包速率为：

\[T=\frac{2-b}{2R}W\ \ \ \ \ \ \ \ \ \left( 5 \right) \]

假设在这个一个周期内，发送窗口的总和为P，则

\[P=nS=\left( \frac{b}{a}W+1 \right) \left( \frac{2-b}{2}W \right) \approx \frac{b\left( 2-b \right)}{2a}W^2\ \ \ \ \left( 6 \right) \]

因此丢包率(丢一个包时)p为

\[p=\frac{1}{P}=\frac{2a}{b\left( 2-b \right) W^2+a\left( 2-b \right) W}\approx \frac{2a}{b\left( 2-b \right) W^2}\ \ \ \ \left( 7 \right) \]

由此可得

\[W\approx \sqrt{\frac{2a}{b\left( 2-b \right) p}}\ \ \ \ \ \ \ \ \ \left( 8 \right) \]

然后，再将8式代入5式得到每秒的平均发包速率为

\[\hat{T}=\frac{1}{R}\sqrt{\frac{a\left( 2-b \right)}{2bp}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{符号替换} \]

\[\hat{T}=\frac{1}{R}\sqrt{\frac{\alpha \left( 2-\beta \right)}{2\beta p}}\,\,\,\,\,\,\,\,\,\,\,\,\ \ \,\,\,\,\left( 9 \right) \ \]

又在TCP传统得拥塞控制算法中，\(\alpha =1\) \(\beta =0.5\) ， \(\hat{T}=\frac{1}{R}\sqrt{\frac{3}{2}\frac{1}{p}}\) 。因此在CUBIC算法中保持这种关系，只有当\(\alpha =\frac{3\beta}{2-\beta}\) 时满足，且\(\alpha\) 为TCP拥塞控制算法窗口增加的加法因子，所以在CUBIC中计算 \(W_{tcp}\)的公式为：

\[W_{tcp}=W_{\max}\left( 1-\beta \right) +\alpha \frac{t}{R}=W_{\max}\left( 1-\beta \right) +3\frac{\beta}{2-\beta}\frac{t}{R} \]

源码分析

/*
 * Compute congestion window to use.
 */  //从快速恢复退出并进入拥塞避免状态之后，更新cnt
static inline void bictcp_update(struct bictcp *ca, u32 cwnd)
{
    u64 offs;//时间差|t - K|
    //delta是cwnd差，bic_target是预测值，t为预测时间
    u32 delta, t, bic_target, max_cnt;

    ca->ack_cnt++;    /*ack包计数器加1   count the number of ACKs */

    if (ca->last_cwnd == cwnd && //当前窗口与历史窗口相同
        (s32)(tcp_time_stamp - ca->last_time) <= HZ / 32)//时间差小于1000/32ms
        return; //直接结束

    ca->last_cwnd = cwnd;//记录进入拥塞避免时的窗口值
    ca->last_time = tcp_time_stamp;//记录进入拥塞避免时的时刻

    if (ca->epoch_start == 0) {//丢包后，开启一个新的时段
        ca->epoch_start = tcp_time_stamp;    /*新时段的开始 record the beginning of an epoch */
        ca->ack_cnt = 1;            /*ack包计数器初始化  start counting */
        ca->tcp_cwnd = cwnd;            /*同步更新 syn with cubic */

        //取max(last_max_cwnd , cwnd)作为当前Wmax饱和点
        if (ca->last_max_cwnd <= cwnd) {
            ca->bic_K = 0;
            ca->bic_origin_point = cwnd;
        } else {
            /* Compute new K based on
             * (wmax-cwnd) * (srtt>>3 / HZ) / c * 2^(3*bictcp_HZ)
             */
            ca->bic_K = cubic_root(cube_factor
                           * (ca->last_max_cwnd - cwnd));
            ca->bic_origin_point = ca->last_max_cwnd;
        }
    }

    /* cubic function - calc*/
    /* calculate c * time^3 / rtt,
     *  while considering overflow in calculation of time^3
     * (so time^3 is done by using 64 bit)
     * and without the support of division of 64bit numbers
     * (so all divisions are done by using 32 bit)
     *  also NOTE the unit of those veriables
     *      time  = (t - K) / 2^bictcp_HZ
     *      c = bic_scale >> 10 == 0.04
     * rtt  = (srtt >> 3) / HZ
     * !!! The following code does not have overflow problems,
     * if the cwnd < 1 million packets !!!
     */

    /* change the unit from HZ to bictcp_HZ */
    t = ((tcp_time_stamp + (ca->delay_min>>3) - ca->epoch_start)
         << BICTCP_HZ) / HZ;

     //求| t - bic_K |
    if (t < ca->bic_K)        // 还未达到Wmax
        offs = ca->bic_K - t;
    else
        offs = t - ca->bic_K;//已经超过Wmax

    /* c/rtt * (t-K)^3 */     //计算立方，delta =| W(t) - W(bic_K) |
    delta = (cube_rtt_scale * offs * offs * offs) >> (10+3*BICTCP_HZ);



     //t为预测时间，bic_K为新Wmax所对应的时间，
     //bic_target为cwnd预测值，bic_origin_point为当前Wmax饱和点
    if (t < ca->bic_K)                                    /* below origin*/
        bic_target = ca->bic_origin_point - delta;
    else                                                    /* above origin*/
        bic_target = ca->bic_origin_point + delta;

    /* cubic function - calc bictcp_cnt*/
    if (bic_target > cwnd) {// 相差越多，增长越快，这就是函数形状由来
        ca->cnt = cwnd / (bic_target - cwnd);//
    } else {//目前cwnd已经超出预期了，应该降速
        ca->cnt = 100 * cwnd;              /* very small increment*/
    }



    /* TCP Friendly —如果bic比RENO慢，则提升cwnd增长速度，即减小cnt
     * 以上次丢包以后的时间t算起，每次RTT增长 3B / ( 2 - B)，那么可以得到
      * 采用RENO算法的cwnd。
      * cwnd (RENO) = cwnd + 3B / (2 - B) * ack_cnt / cwnd
     * B为乘性减少因子，在此算法中为0.3
     */
    if (tcp_friendliness) {
        u32 scale = beta_scale;
        delta = (cwnd * scale) >> 3; //delta代表多少ACK可使tcp_cwnd++
        while (ca->ack_cnt > delta) {        /* update tcp cwnd */
            ca->ack_cnt -= delta;
            ca->tcp_cwnd++;
        }

        if (ca->tcp_cwnd > cwnd){    /* if bic is slower than tcp */
            delta = ca->tcp_cwnd - cwnd;
            max_cnt = cwnd / delta;
            if (ca->cnt > max_cnt)
                ca->cnt = max_cnt;
        }
    }

    ca->cnt = (ca->cnt << ACK_RATIO_SHIFT) / ca->delayed_ack;
    if (ca->cnt == 0)            /* cannot be zero */
        ca->cnt = 1; //此时代表cwnd远小于bic_target，增长速度最大
}

巨人的肩膀

http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.153.3152&rep=rep1&type=pdf

http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.37.7442&rep=rep1&type=pdf

https://blog.csdn.net/dog250/article/details/53013410