引言
本为主要对我在开发JAVA黑白棋人机算法过程中所用的博弈思想、估值函数、搜索算法分3个方面进行了阐述,由于本人水平有限,如果大家希望了解更多有关黑白棋博弈策略以及人机算法的深入的理论研究,可以参看本文最后的参考文献,或者搜索其他相关资料。
黑白棋,又叫反棋(Reversi)、奥赛罗棋(Othello)、苹果棋或翻转棋。黑白棋在西方和日本很流行。游戏通过相互翻转对方的棋子,最后以棋盘上谁的棋子多来判断胜负。它的游戏规则简单,因此上手很容易,但是它的变化又非常复杂。有一种说法是:只需要几分钟学会它,却需要一生的时间去精通它。(本段摘自百度百科)
正文
一、黑白棋人机博弈思想
1.棋局阶段应合理划分(一般分为三个阶段),开局应尽量用优秀的定式
之所以要使用开局定式,个人的观点为:即使最顶级的机器能够从第一步一直搜索到最后一步,也必然不能断定谁最终会赢,要不然这个游戏就没有存在的价值了。
基于上面的观点,必然走到某一种局面的时候,才可以断定输赢,当然这个输赢不是绝对的,更不是最终意义上的输赢,因为对方有可能不按最优路线行棋。于是我们便需要利用优秀的开局为自己争取尽可能大的优势,迫使对方失误或者为自己争取胜利的保障。
2.稳定子具有绝对优势
所谓稳定子,就是指再后续的行棋过程中始终不会被翻转的棋子。最明显的稳定子就是角位置的棋子,同时当角位置被占取之后,角周围的棋子,尤其是两条边上的,也会较容易成为稳定子。棋局终了时棋盘上的所有子都可以看做是稳定子。
当然,稳定子有绝对的优势,并不意味着我们见角就夺,比如斯通纳陷阱就是一个很好的例子。
3.内部子具有相对的优势
所谓内部子,就是被一方的棋子围困在内部的另一方的棋子。
内部子的优势主要体现在:①内部子是半稳定子或者稳定子,不易被对方吃掉;②拥有较多的内部子,可以提高己方的行动力(可下子位置的数量),限制对方的行动力,从而更容易设置陷阱,迫使对方走出很差的棋步,进而使自己占有一定的优势。
4.边缘子具有相对的劣势
所谓边缘子,可以看作是除去边角之外的周围有空位的棋子,或者可以理解为包围内部子且与内部子异色的周围有空位的棋子。
边缘子实际上是相对于内部子而言的,因为边缘子的劣势也恰好是与内部子相对的:①边缘子在现有棋局下多数是不稳定的,但在后续行棋过程中可能成为对方或者己方的稳定子;②为对方制造陷阱提供了更多的机会。
5.奇偶性理论
所谓奇偶性,就是指如果在对弈过程中没有任何一方停步,那么当黑棋下完后,棋盘总会有奇数个空位,而当白棋下完后,棋盘总会有偶数个空位。
我们可以推断,如果没有任何一方停步,那么白棋会走完最后一步棋并应该略微占优一定的优势。但如果有一方停步时,这个奇偶性就会颠倒过来,当再有一方停步的时候,奇偶性就又会恢复正常。
因此,黑棋总是希望构造强制性的奇数次停步。同时,黑棋想要获得奇偶性的优势的另外一个可行的办法就是:建立一种这样的局面,使得每次黑棋下完之后棋盘上有且仅有奇数个拥有奇数个空位的空白区域,并且这些区域是白棋无法进入的,或者一旦白棋进入,黑棋就会拥有绝对的优势。
二、机器容易实现的评判棋局优劣的因素,以及估值函数的实现
既然要评判棋局的优劣,那么就必然要想破译密码那样把棋盘上所有棋子的分布转化成一个数值,以数值的大小来衡量己方的收益情况,而转化的方式就是估值函数。
一般估值的形式有以下两种:
①采用概率的思想,数值的取值范围为[0,1],确定为胜局时值为1,败局时值为0,平局时值为0.5。假设当前无法判断输赢,对棋局的评估值计算后为a,那么综合值就是0.5+a。也可优化一下,把取值区间看做[-1,1],这样确定胜局时值为1,败局时值为-1,平局时值为0。
②将概率思想中的实数整数化,即对概率值乘以INF,这样取值区间就变成了[-INF,INF]。
估值函数这个模块是整个程序中最核心的一个模块,之所以这样说,是因为无论怎样优化搜索过程,在现有的条件下搜索层数也是有限的,如果这个模块没有做好,很容易出现这样的过程:不能确定输赢,取最优-->……-->不能确定输赢,取最优-->发现自己一定会输。当然,我们期望的过程是这样的:不能确定输赢,取最优-->……-->不能确定输赢,取最优-->发现自己一定会赢。
想要尽可能出现我们期望的过程,那么一般便有三种措施:一是选用优秀的开局定式,二是提高估值函数模块的性能,三是通过对搜索算法的优化来加深搜索层数。
对于选用优秀的开局定式,是受到百度百科上对一款外国棋力顶尖的黑白棋软件的简介的启发,但对于如何存储和实现开局定式,我还只是处于萌芽阶段,在此就不妄加分析了。对于对搜索算法的优化,我会放在下一个版块来阐述一些我的学习的心得。
下面就主要阐述一下我对如何让机器对人考虑机博弈思想并实现对棋局进行评估的一些看法,也即对提高估值函数这个模块的性能的一些看法。
1.对稳定子的考虑
对稳定子的考虑在理论上是很有意义的,因为最终棋局比的实际上还是稳定子的数量,但对稳定子进行判断这个过程是不容易实现的,而且我在一个论坛上也看到有个帖子说,在高强度的对局中,一般都要四五十步之后才会出现稳定子,而这时搜索函数已经可以搜索到底了。基于这一点,对稳定子判断的意义也就体现在40-60步中还不能确定谁输谁赢的情况。
考虑到这些,我决定放弃对稳定子的判断而转化成两个部分,一个是对边角位置利用权值表去判断己方的收益,另一个就是对中间部分的位置,转化成对内部子与边缘子的考虑,因为内部子、边缘子与稳定子之间是有一定的联系的。
2.对边角位置的考虑
说起权值表,我们肯定很容易想到角位权值大,而C位(与角相邻的边上的位置)和星位(与叫相邻的除去C位之后剩下的那个位置)的权值小。但对权值表的设定过程中,还要注意一些细节:
①为了方便计算,不妨把对己方有力的位置的权值取正,对己方不利的位置的权值取负,这样在运算时只需要各个值取相反数,就成为了对方在行棋时对我方收益而言的一张权值表,这样便只需要做一张权值表就可以了。
②对于各个位置权值的确定是要综合各种情况并不断试验的,但同时也要符合一些基本的逻辑。比如我们设角位的权值为a(a>0,对己方有利),星位的权值为b(b<0,对己方不利),那么应该有a+b>-b,因为如果a+b<-b,那么我们可以将其变形成-a-b>b,也就是说对方同时占角位和星位为我们带来的收益要大于我们只占一个星位而来带来的收益(这里的收益都是负值),也就是说,电脑宁肯让对方占一个角位和一个星位,自己也不会去只占那个星位而不占角位,这显然在大部分情况下是不符合逻辑的。
结合我个人针对自己的程序研发的权值表以及一张外国人研发的权值表,对其中有些值进行了修改,生成了一张新的权值表,也就是在v4.7中使用的权值表。权值表如下:
{100, -5, 10, 5, 5, 10, -5,100},
{ -5,-45, 1, 1, 1, 1,-45, -5},
{ 10, 1, 3, 2, 2, 3, 1, 10},
{ 5, 1, 2, 1, 1, 2, 1, 5},
{ 5, 1, 2, 1, 1, 2, 1, 5},
{ 10, 1, 3, 2, 2, 3, 1, 10},
{ -5,-45, 1, 1, 1, 1,-45, -5},
{100, -5, 10, 5, 5, 10, -5,100}
3.对内部子和边缘子的考虑
由于内部子和边缘子是相对的,在对程序要求不是很高的情况下,我们可以只研究其中一方。同时,结合实战经验,边缘子数量对棋局的影响程度要高于内部子,因而我们不妨抓住主要矛盾去研究边缘子的多少。
在对边缘子的研究过程中,我又研发了另一种间接统计边缘子的方式,即统计一个边缘子周边的空格数,然后取相反数(边缘子越多,一定程度上对己方越不利)作为这个边缘子的权值。之所以这么做,是希望能够融合对行动力(可落子位置的总数)的考虑,因为边缘子周围空位的数量一定程度上体现了对方行动力的大小。但后来在实际应用过程中,这种想法并没有达到我预想的效果,可能是因为对不同的情况,二者之间的线性关系并不明显,于是我便转而只单纯地去考虑边缘子的数量。
4.对奇偶性理论的考虑
因为对于这个部分,代码实现起来比较困难,所以我并没有把这个部分的理论应用到我的程序之中。但就百度百科上的资料显示,国外一个十分强大的黑白棋软件是把棋手行棋是否具有奇偶性也纳入了考虑范围之内的。
5.对可以搜到最终结果的情况的考虑
当机器可以搜到最终结果时,我们就不宜再用权值表等统计权值的方法来衡量棋局的优劣,因为最终子数多者一定获胜,但依棋局的估值函数,算出的权值却不一定时较大者。
因此,当可以搜索到最终结果时,我们便需要对估值函数的返回值做修改:
①如果我们选择的是取值为[-1,1]的实数概率的估值函数,那么当确定自己获胜的时候就可以返回1,失败时返回-1,平局时返回0。当然,更为方便的方法就是直接返回己方与对方的棋子数之差,同时,出于对规则的考虑,我们也要这么做,因为现行的规定是:双方分先下偶数局数的棋(如4局),胜1分,负0分,和0.5分,分数多的取胜,假如分数一样,就以棋子数目来计算胜负。于是,确定为赢时,我们赢得棋子越多越好,而确定会输的时候,输得越少越好。
②如果我们选择的是取值为[-INF,INF]的整数化概率的评估函数,那么当确定自己获胜时返回INF+己方与对方棋子之差,确定自己失败时则返回-INF+己方与对方棋子之差,平局时返回0。
6.估值函数的实现(也即对各项影响棋局因素的权值进行合并)
当可以搜索到最终结果的情况我们已经在前面讨论过了,因而在这里我就主要阐述一下对在搜索过程中无法得到最终结果时估值函数的实现的一些看法。
我们不妨设各项因素的权值分别为a1,a2……an,如果采用的是实数概率值的估值函数,那么一般同时满足-1
在合并的时候,按是否线性合并可以分为下面两种合并方式:
①非线性合并
若执行非线性合并,其优点在于最后的估值会更加精准,毕竟大多数涉及概率的函数都是非线性的,但缺点在于非线性合并的函数形式是比较难确定的。同时,因为涉及到整数进行非线性运算的精度的问题,如果采用整数化概率值的估值函数,是不宜使用非线性合并的。
②线性合并
线性合并的优点在于函数形式是确定的,我们后续的工作就是确定出各项的前导系数就可以了。
我们设线性合并公式中各项的前导系数分别为p1,p2,……,pn,那么最终的估值就是value=p1*a1+p2*a2+……+pn*an,并且如果选择的是实数概率的估值函数,那么一般还会满足p1+p2+……+pn=1。
出于容易实现这一角度的考虑,我还是选用了线性合并,由于我只考虑了每个位置的权值和边缘子的数量,如果两个因素的权值分别为a1、a2,那么我的程序的估值函数的形式就是value=p1*a1+p2*a2。
在选择了线性合并之后,那么最大的难题就在于确定p1与p2的值。在猜测两个参数的值时,我遵循了两条原则:①衡量各项估值之间的大小差异,做到尽量平衡,但又有所侧重;②选取尽量小的整数作为pn的值,这样需要测试的情况的种数也会减少很多。
通过这样的猜测和测试,最终v4.7采用的p1与p2的值分别为3和7。
三、黑白棋博弈树搜索算法及其实现
1.Min-Max搜索
在机器与人对弈的过程中,机器事先并不知道人的水平如何,因而机器只能假设人走的每一步都会为自己带来最小的收益,而机器走的每一步都要为自己争取最大的收益,这就是极大极小原理。
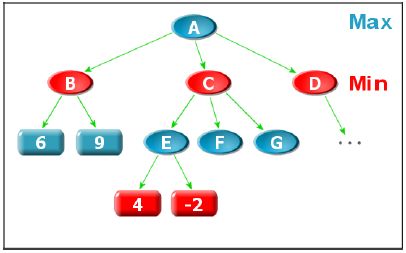
如果我们把机器和人接连走的每一步画成树状结构的话(也即博弈树,见上图),对于每一个节点,其子节点是下一步所有可能走的位置(有可能是对方走,也有可能是自己走),对于叶子节点我们运用一次估值函数得到叶子的权值,之后便一直向上反推,直到得到根节点的权值。我们把每一次机器要走的节点叫做Max节点,因为这个节点的值是其子节点所有值中的最大值,而把每一人要走的节点叫做Min节点,因为这个节点的值是其子节点所有值中的最小值。这样得到的根结点的值,就是机器走这一步的期望的最大收益。
基于这样的算法,我们进行迭代深搜是可以实现的。深搜函数的返回值对于Max节点而言就是所有子节点的最大值,而对于Min节点而言就是所有子节点的最小值。
同时,在深搜过程中,我们要不断更新、记录棋盘的状态,但对于黑白棋而言,比较棘手的一个问题就是自己每下一步,不仅会改变己方棋子的分布,同时还会改变对方棋子的分布,这样对于将下过一个棋子的棋盘还原成没下之前的棋盘是十分困难的,因而我们不能采用传统的深搜函数的形式(对访问位置做标记,深搜并得到返回值,抹去对访问位置的标记),于是我们在迭代的时候就要不断new一个数组来存储变化之后的棋盘,并作为深搜函数的参数,传递给下一个节点。
由于深搜节点的数量是指数级增长的,如果我们不对深搜层数进行一定的限制,那么程序的运行时间将是一个很庞大的数字。对于未加优化的的搜索,如果限定30s之内要行棋的话,最坏情况也只能搜索5层左右,因而我们必然要对Min-Max搜索算法进行优化,来提升程序的棋力,一种有效的方法就是对Min-Max进行α-β剪枝优化,也就是接下来要讨论的α-β搜索。
现在先抛开优化搜索算法的问题,我们在使用Min-Max搜索算法编出的程序时,会发现往往最后结局电脑往往会很快就能走出一步棋,原因在于到了后期,博弈树每层的节点数很变得很少,而这时机器完全有时间做出更深层次的搜索,因而我们可以采用用限定搜索节点的方式来取代限定搜索层数的方式进行深搜,这样我们就可以充分利用现有的时间,当节点多时就少搜几步,而当节点少时就多搜几步。具体实现的方法就是取一个变量branches记录当前节点还可以向下搜索的总节点数,而对当前节点的子节点进行深搜时,传递过去的参变量就变成了branches除以当前节点拥有的子节点的数量,当branches为0或者双方都无子可下时,就要调用估值函数了。
2.α-β搜索
前面已经说过了,α-β搜索实际上就是运用α-β剪枝优化后的Min-Max搜索,其基本的极大极小的思想是不变的。
我们首先引入两个变量α、β,表示当前节点在前面的深搜过程中,依据子节点的返回值来估计出的当前节
点最后的结果的下限和上限。
以下图为例,我们来讨论一下α-β搜索剪枝的原理:
首先,我们初始化A点的下限为-INF,上限为INF,要知道A点的值就要搜索B点,搜索B点后得知B的值为6,那么我们就可以更新A点的下限为6,因为A点是Max节点,也即A点的α值为6。这时我们继续搜索C点,我们将A点的下限6和上限INF同时作为参数传给子节点C,显然C的值至少要在6和INF之间A才有可能更新成C的值。要知道C点的值我们就要继续搜索E点,同样把下限6和上限INF传递给点E,显然E要在6和INF之间,C点的值才有可能在6和INF之间,那么A点才有可能更新成C点的值。而搜索E点时我们发现E点值为-2,不在6和INF之间,这时我们还有必要搜索F和G点吗?显然没有必要,因为反正A是不会更新成C的值了,我们当然没必要多搜索F和G了。
上面不去搜索F和G的过程就是剪枝的过程,确切来说是α剪枝的过程。下面就给出α剪枝和β剪枝的定义:
①如果当前节点是Min节点,当前节点的父节点是Max节点,那么当当前节点的一个子节点的值小于当前节点的α值时,那么当前节点的其余子节点就不用搜索了,这个过程称为α剪枝过程。
②如果当前节点是Max节点,当前节点的父节点是Min节点,那么当当前节点的一个子节点的值大于当前节点的β值时,那么当前节点的其余子节点就不用搜索了,这个过程称为β剪枝过程。
通过上面的实例,我们也观察到,当前节点α、β的值是不断依据子节点的返回值进行更新的,并作为深搜函数的参数进行下一个子节点的深搜。其中根节点的α、β的值分别初始化为-INF、INF。
一般来说,当前节点是Min节点时,如果子节点的返回值小于当前节点的β值,那么β值就会更新成为返回值,当返回值同时小于或者等于当前节点的α值时,如果同时当前节点的父节点是Max节点,就会产生剪枝的过程。
同样的,当前节点是Max节点时,如果子节点的返回值大于当前节点的α值,那么α值就会更新成为返回值,当返回值同时大于或者等于当前节点的β值时,如果同时当前节点的父节点是Min节点,就会产生剪枝的过程。
我们发现上面讨论的两种情况都是当前节点与父节点不是同类节点的情况,那么如果当前节点和父节点是同类节点呢(也即发生了停步的情况)?这时就没办法进行剪枝了。
通过上面的讨论,我们注意到,在深搜的过程中,我们同时要用一个参数来传递父亲节点的类型,如果父亲节点和当前节点是同类节点时,即便满足了一部分的剪枝条件,也是不能进行剪枝的。
后记
黑白棋的人机算法是博大精深的,一直到v4.7这个版本我才只是刚刚研究到最基本的对Min-Max搜索的优化,还有更多的诸如历史表和置换表以及启发式搜索等优化方法还有待进一步学习。
通过这次黑白棋项目的实践,我由衷的感觉到了算法的重要性,以后还要在ACM竞赛的准备中不断学习更多的算法并应用到软件开发中来。机器的优势在于快速而精准的暴力,而算法的作用就在于使其在有效实时间和空间内,尽可能地多得发挥它的优势。
参考文献
[1] 柏爱俊.几种智能算法在黑白棋程序中的应用.
[2] 黑白棋对弈策略指南-玄黄整理版
[3] 黑白文档
P.S. 黑白棋游戏的jar文件我挂在了另一篇博客《JAVA黑白棋之学习感悟》的下面,大家
可以下载下来玩一玩哈。如果有什么意见或者建议,还望各位不吝赐教哈O(∩_∩)O~