定长字符串匹配

奇怪的字符串匹配

1.题目：

字符串匹配 (100分)

给出一个最大长度为10^6的母串t，请你在t里面找到长度为len的出现次数最多的子串，如果找到多个出现次数一样的子串，请你输出字典序最小的。

输入格式:
在第一行输入一个正整数Len（Len<=10⁶），第二行输入一个母串t，t的长度小于等于10⁶

输出格式:
输出答案子串和它在t中的出现次数，用一个空格分隔，行末尾没有多余空格！

输入样例:
3
aba ababababababaaababababa

输出样例:
aba 11

时空限制

时间限制 ：2000 ms
内存限制 ：256 MB
注意空间的大小

2.题目分析：

我不熟悉像KMP，BP，Sunday这样的字符串匹配算法，看见题目第一感觉就是hash，内存给的不要太大。
对每一个子串求hash，如果位置是空的就给malloc一个节点，有东西就判断一下是不是等于我现在要插入的字符串，不是就冲突了。

void insert(char *x){
    int crash = 0;
    int hs = hash(x, crash);
    while (1){
        if (!table[hs]){
            table[hs] = malloc(sizeof(struct Node));
            table[hs]->cnt = 1;
            table[hs]->t = x;
            return;
        } else if (equal(table[hs]->t, x)){
            table[hs]->cnt++;
            return;
        }
        hs = hash(x, ++crash);
    }
}

不就完事了，最后统计一个字典序最小。一次作业就又水过去了(0.0)。
但是这题，花了十几个小时做hash优化。。。

3.爬坑过程：

记录一下爬坑的过程，如果不想看可以直接跳到下一部分

step.1

刚学hash没多久，就想着按着书本的方式，写一个hash函数，用链表来解决冲突，一计超时拍我脸上
之后一想估计是冲突解决的方案不太行
就改成了平方探测法， 就像下面这样

int hash(const char *x, int crash){
    if (crash){
        return (cache[x-s] + crash) % TABLE_SIZE;
    } else {
        unsigned long long sum = x[0];
        for (int i = 1; i < len; i++) {
            sum = (sum << 2) + x[i];
            sum %= TABLE_SIZE;
        }
        return sum;
    }
}

还超时，，，

step.2

是不是冲突太多次了，每次都算hash太慢，我整个数组存一下是不是就行了？
赶紧用个cache数组缓存一下数据

int cache[MAX_T_LEN];
int hash(const char *x, int crash){
    if (crash){
        return (cache[x-s] + (crash%2 ? 1: -1) * (1 << (crash-1)/2)) % TABLE_SIZE;
    } else {
        unsigned long long sum = (int)x[0];
        for (int i = 1; i < len; ++i) {
            sum = (sum << 2) + (int)x[i];
            sum %= TABLE_SIZE;
        }
        cache[x-s] = (int)sum;
        return cache[x-s];
    }
}

是不是每次都mod表长，太花时间了，毕竟是个除法

// 这个F设成全局变量，只要算一次
unsigned long long F = 0;
F = ~F; F = F>>2;

if (sum & F) sum %= TABLE_SIZE;

就是用位运算来判断一下我是不是要对表长取模了
解释一下，看之前的代码可以知道我是对sum左移两位来计算hash的，那么我只要判断一下最前头两位是不是有1了
比如 0111 1111 0101 0101，最前两位有一个1，要溢出了呀，根据取余一下.
if里用个按位与操作，F差不多是这样的 1100 0000 0000 0000，这样按位与 一下前面的sum就可以取出前面两位了

是不是比较字符串相等的时候太慢了，再来位运算

int equal(const char *a, const char *b){ //比较字符串是否相等，相等return 1
    if (a == b) return 1;  // 地址一样肯定是相等了
    for (int i = 0; i < len; ++i) {
        if (a[i]^b[i]) return 0;
    }
    return 1;
}

啊啊啊，还是超时！！！(又是最后一个点)事实证明，花里胡哨没什么用。

step.3

启动终极计划>>>>>把代码发给大佬
大佬说，散列表内部最好根据字典序对字符串排序，这样第一个出现次数等于max的就是答案了
省去了比较字符串大小的操作。
可是我不会呀，绞尽脑汁想出了一个hash表里套hash的方法。
就是"abcddd"过来了，放在table[1][2][3]这个hash表里，"bccc"放在table[2][3][3]这个表里
这样一来下标越小的字典序肯定小，问题就解决了。
最后绕来绕去，把我绕晕了，写了个0分

最后我干脆,把比较函数删了，管什么字典序
还是超时！！！
说明程序的时间卡在了hash相关的部分，而不是对字符串的排序。

重新考虑一下程序结构，一不做二不休，把比较两个字符串是不是相等的部分删了

void insert(char *x){
    int hs = hash(x);
    if (!table[hs]){
        table[hs] = malloc(sizeof(struct Node));
        table[hs]->cnt = 1;
        table[hs]->t = x;
    } else { // 设永远不会冲突
        table[hs]->cnt++;
    }
}

这个代码虽然答案错误，但他快的起飞，终于不再是运行超时了
现在问题的关键重新转移到了编写一个优秀的hash函数，让假设在大多数情况下成立

pass
稍稍总结一下上面的花里胡哨的优化
1.使用位运算代替简单却多次使用的语句
测试证明在比较两个字符串是否相等的算法中使用"&“会比”=="快20-30%
2.使用cache数组缓存可能多次用到的运算值
这是一个很常用的方法来用时间换取时间，有些时候同一个运算结果会被多次使用
重用次数越多效率提升越明显
3.某些循环的结束是需要计算的值，用一个变量缓存这个值，会提升循环效率，这是个好习惯
可以看下面的代码

for (int i = 1, end = s_len-len+1; i < end; ++i) {
    insert(s+i);
}

显然，如果每一次都计算end，会浪费一下算力， 只用一个int的空间就可以减少n次的额外运算
当代码运行在嵌入式设备是，这样的细节很关键

4.最终效果

通过截图

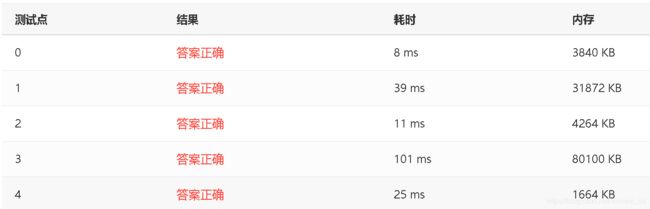
最后的通过代码使用了二维的哈希表，同时散列了2个值，分别对应表的二个维度
这样大大降低了碰撞的可能性，虽然会增加一些运行时间。
代码中不再对字符串进行比较，也就是假设hash不会冲突，不写冲突解决的代码
虽然这样做有可能会出现错误的答案，但在大多数情况下是正确的
这和MD5摘要算法一样保证的绝大多数情况下都不会出现两个源串会有同一个hash值
如果还不放心可以加大表长，甚至使用3维乃至n维的表
总的来说这是一个可行的算法，它有着较好的效率

核心算法

自然溢出法

对于C/C++(和一些其他语言) unsigned int 和unsigned long long,这些无符号的整型，加法或乘法会导致数据溢出
这效果等价与对2^{sizeof(TYPE)*8}取模，下面用unsigned long long举例子

unsigned long long a, c = 0;
c = ~c;   //c = 2^32-1
printf("MAX: %llu\n", c);
printf("MAX+1: %llu\n", a = c + 1); // 输出了0
c = c/2 + 1;  // 试试乘法
printf("2^31 * 2^32:%llu\n", a = c * c);

运行截图:

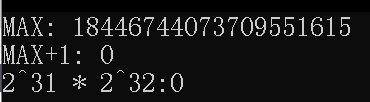
用自然溢出法省去了在计算hash过程中的取模运算,还是能节省一些运行时间的
但记得最后还是要对表长取模的

二维哈希表

二维的哈希表和普通的哈希表一样，只不过用2个不同的hash函数，对应2个维度，减少碰撞发生
以下用字符串的进制hash做例子

// 一般的hash
hash[i] = hash[i-1]*P + src[i];
// 这样用
table[hash[i]];

// 二维的hash
hash[x] = hash[x-1]*P + src[i];
hash[y] = hash[y-1]*P + src[i];
// 这样用
table[hash[x]][hash[y]];
// 最后要根据直接的算法对表长取余，或者用自然溢出法

对一块固定大小的内存，二维表的TABLE_SIZE_X和TABLE_SIZE_Y可以取sqrt(MAX_SIEZ)附近的素数
进制数P要求不高，可以自己尝试

进制hash(补充)

进制hash是我在程序中使用的hash策略，是下面正对题目优化的基础
进制hash一般来说是针对字符串的一种hash策略
来看看下面的代码, 我们用"123"来做例子，并且将进制数P设为10

char src[] = "123";
int len = 3;  //实际长度是4,'\0'当然不用计算hash
unsigned long long hash = 0;
const unsigned long long P = 10;
for (int i = 0; i < len; i++){
	hash = hash*P + src[i]-'0';
}
printf("hash: %llu\n", hash);

显然会输出123
这就是进制hash，用一个进制数来对前一个部分的hash值做累成，再加上现在的值
在例子里，'1’被乘上了10²,'2’被乘上了10¹,'3’被乘上了10⁰，10就是进制数P
只要把上面的代码，P改为你设置的进制数，且src[i]-‘0’改为src[i]-’ '或其他，就可以计算一个字符串的hash
这就是字符串的进制hash，和普通的十进制，十六进制是完全类似的

针对题目对hash函数的优化

进制hash O(1)求子串hash
对于进制hash有一个方法可以在O(1)的时间内求得子串的hash值：
hash=((hash[r]−hash[l−1]∗P^r−l+1)%mod+mod)%mod

l,r分别是子串的左右下标,P是进制数,mod可以是表长或者自然溢出法的2⁶⁴
简单验证一下：
先求"abcd"的hash，设P=10,src[i] = s[i] - ‘a’ + 1
那么"a"的hash就是1,"abcd"的hash就是1234
我们求"bcd"的hash,根据公式，hash[“bcd”] = hash[“abcd”] - hash[“a”]*10³
算出来就是234，发现正确。

但那mod又是拿来干嘛的呢？
如果这字符串很长，根据上面的直接算法，很有可能就超过了int,long long这些类型的范围
而导致溢出成负数，两次取模运算就是让hash始终为正。
进制法的hash对一个数取模居然不影响上面这个规则的成立，怎么证明我不知道，
如果你会请记得写下你的评论哦

对于题目

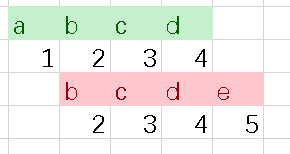
我们先进行初始化算出了abcd的hash是1234
现在用上面的公式递推就好了，可以算出bcde的hash是2345
这样极大优化了时间复杂度，对一个子串，复杂度从O(n)到了O(1)
对于程序需要处理每一个子串，复杂度从O(n²)降到了O(n)

对哈希表的一点理解

都知道，表长一定要选素数！！！
除了用二维的哈希表，如果必要你可以用更多维数的表，不过一般二维的足够了
hash表的关键是对hash函数的选择，要对每一种类型都特殊对待(字符串，数字还有其他)
表长越大冲突越少，典型的空间换时间
自然溢出真香
hash还有和二分一起的高端操作，别问，问就是 不会
听说ACM会卡hash的某些常用素数
进制数也最好选素数

5.代码

代码很烂，看看就好

// warning: Use UTF-8 encoding
/*
 * 程序使用二维的哈希表，来降低碰撞几率
 */

#include 
#include 
#include 
#define TABLE_SIZE_X 4001
#define TABLE_SIZE_Y 4027

const unsigned long long P_X = 293;
const unsigned long long P_Y = 17;
#define MAX_T_LEN 1000009

struct Node* table[TABLE_SIZE_X][TABLE_SIZE_Y];
int max = 1;
int len, s_len;
char s[MAX_T_LEN];
int index_len = 0;
int survive_index_x[MAX_T_LEN], survive_index_y[MAX_T_LEN];

struct Node{
    int cnt;
    char *t;
};

unsigned long long back1, back2;
unsigned long long p_pow_len1, p_pow_len2;
// 无符号长整型乘法溢出规则为，c = a*b % 2^64
void hash(const char *x, int *a, int *b){
    back1 = (back1*P_X - (s[x-s-1]-31)*p_pow_len1 + x[len-1]-31);
    back2 = (back2*P_Y - (s[x-s-1]-31)*p_pow_len2 + x[len-1]-31);
    *a = (back1 % TABLE_SIZE_X + TABLE_SIZE_X) %TABLE_SIZE_X;
    *b = (back2 % TABLE_SIZE_Y + TABLE_SIZE_Y) %TABLE_SIZE_Y;
}

int cmp(const char *a, const char *b){
    for (int i = 0; i < len; i++){
        if (a[i] > b[i]) return 1;
        else if (a[i] < b[i]) return 0;
    }
    return 0;
}

void insert(char *x){
    int a, b;
    hash(x, &a, &b);
    if (!table[a][b]){
        table[a][b] = (struct Node*)malloc(sizeof(struct Node));
        table[a][b]->cnt = 1;
        table[a][b]->t = x;
        survive_index_x[index_len] = a;
        survive_index_y[index_len++] = b;
    } else {    // 假设不会发生冲突
        table[a][b]->cnt++;
        if (table[a][b]->cnt > max){
            max = table[a][b]->cnt;
        }
    }
}

int main(){
    // 输入
    scanf("%d", &len);
    getchar();
    gets(s);
    s_len = strlen(s);
    s[s_len] = 0;
    // 初始化
    back1 = s[0]-31;
    back2 = s[0]-31;
    p_pow_len1 = P_X;  p_pow_len2 = P_Y;
    for (int i = 1; i < len; i++) {
        p_pow_len1 *= P_X;
        p_pow_len2 *= P_Y;
        back1 = back1*P_X + (s[i] - 31);
        back2 = back2*P_Y + (s[i] - 31);
    }
    int x0_t = back1 % TABLE_SIZE_X;
    int y0_t = back2 % TABLE_SIZE_Y;
    table[x0_t][y0_t] = (struct Node*)malloc(sizeof(struct Node));
    table[x0_t][y0_t]->cnt = 1;
    table[x0_t][y0_t]->t = s;
    survive_index_x[index_len] = x0_t;
    survive_index_y[index_len++] = y0_t;
    // 将子串插入hash表
    for (int i = 1, end = s_len-len+1; i < end; ++i) {
        insert(s+i);
    }
    // 若有多个出现次数相等的子串 则比较，找出最字典序小
    int min_x = survive_index_x[0];
    int min_y = survive_index_y[0];
    for (int i = 1; i < index_len; ++i) {
        int index_x = survive_index_x[i], index_y = survive_index_y[i];
        if (table[index_x][index_y]->cnt == max){
            if (cmp(table[min_x][min_y]->t, table[index_x][index_y]->t)){
                min_x = index_x;
                min_y = index_y;
            }
        }
    }
    // 输出结果
    table[min_x][min_y]->t[len] = 0;
    printf("%s", table[min_x][min_y]->t);
    printf(" %d\n", max);
    return 0;
}

6.感悟

这题花了我十多个小时，提交次数达到了惊人的180次。但都是值得，我对哈希表的理解有了很大提升。也真的做了一次时空的权衡

欢迎留下你的精彩评论！