1、有a,b,c,d四个人,其中一个是小偷;a说我不是小偷,b说一定是c,c说小偷是d,d说c在胡说八道;
其中三个人说的真话,一个人说的假话,请用编程得出谁是小偷
def thief_is():
for thief in ('a', 'b', 'c', 'd'):
sum = ('a' != thief) + (thief == 'c') + \
(thief == 'd') + (thief != 'd')
if sum == 3:
print("thief is %s"%thief)
thief_is()
2、有n阶台阶,一次可以跳1级,也可以跳2级,。。。也可以跳n级;那么跳上第n阶有几种方式,请用编程求出结果
def calnum(num):
if num <= 1:
result = 1
else:
result = num * calnum(num-1) # 函数内部调用自己
return result
print(calnum(1))
3、有一个列表,请使用编程实现对它的反转,直接修改原列表,不用内置方法
l = [1,2,3,4,5,6]
l1 = []
for i in range(len(l)):
l1.append(l[-i-1])
print(l1)
4、有模块B,其中有一个prinit("B");
模块A、C都导入了B;
启动文件main.py中,导入了A和C;
问prinit("B")被执行了几次
1次 单例模式,只有在首次导入时才会加载
5、数据库中有一个自增的用户表,用户名有重复的,请用sql命令删除重复的记录,并随机保留一条
假设有一样一张数据库表TNames,有两个字段 ID:主键 int;Name:nvarchar(50)
TNames表中有一些重复数据行 例如:
ID Name
---------------------------
1 wang
2 wang
3 lee
4 lee
5 lee
6 zhang
7 zhang
8 zhao
现要求从这张表删除重复的记录,结果要求为:数据表中最后剩下wang、lee、zhang、zhao四条不重的记录。
解题思路:1)首先要找到重复的Name 执行Sql为
select Name from TNames group by Name having count(*)>1
2)其次根据上一步的Sql找到每一组重复Name的最大ID或最小ID 执行Sql为
select max(id) from TNames where Name in(select Name from TNames group by Name having count(*)>1) group by Name
3)根据上两步查询删除TNames表中条件为 Name 包括在第一步执行Sql中,且ID不包括第二步执行Sql中的记录,具体Sql语句为
delete from TNames where id not in(
select max(id) from TNames where name in(
select name from TNames group by name having count(*)>1) group by name) and name in (select name from TNames group by name having count(*)>1)
经过第3步的执行,便可以从数据表中清除重复的记录。
6、有一个单链表,请用编程实现单链表的反转
class Node(object):
def __init__(self, data, next=None):
self.val = data
self.next = next
def fun4(head):
if head == None:
return None
L, M, R = None, None, head
while R.next != None:
L = M
M = R
R = R.next
M.next = L
R.next = M
return R
if __name__ == '__main__':
l1 = Node(1)
l1.next = Node(2)
l1.next.next = Node(3)
l1.next.next.next = Node(4)
print(type(l1))
print(type(l1.next))
print(type(l1.next.next))
l = Node.fun4(l1)
print(l.val, l.next.val, l.next.next.val, l.next.next.next.val)
7、如何实现数据库的热备份,并且由原来的表变成四个表
8、sqlalchemy的使用,关于阻塞的,我不记得具体问题了
9、用Python实现单链表,并实现它的逆序
10、用python中序遍历一个二叉树
先创建一颗二叉树:
class BinaryTree:
def __init__(self, data):
self.data = data
self.left = None
self.right = None
def get(self):
return self.data
def getLeft(self):
return self.left
def getRight(self):
return self.right
def setLeft(self, node):
self.left = node
def setRight(self, node):
self.right = node
好,这里我们定义好了一个二叉树类,并给它添加了一下方法,然后我们来实例化一颗二叉树:
binaryTree = BinaryTree(0)
binaryTree.setLeft(BinaryTree(1))
binaryTree.setRight(BinaryTree(2))
binaryTree.getLeft().setLeft(BinaryTree(3))
binaryTree.getLeft().setRight(BinaryTree(4))
binaryTree.getRight().setLeft(BinaryTree(5))
binaryTree.getRight().setRight(BinaryTree(6))
实例化好的二叉树是长这个样子的:
中序遍历的顺序是:先遍历树的左节点,再遍历树的父节点,再遍历树的右节点。
对于我们上面创建的二叉树,它的中序遍历结果就是:3 -> 1 -> 4 -> 0 -> 5 -> 2 -> 6
在前序遍历的时候是先遍历父节点,所以result.append(now.data),就在遍历左节点和右节点的前面。
而中序遍历要先遍历左节点,所以result.append(now.data)就要在遍历左节点的后面,遍历右节点的前面。
def intermediateTraversal(now, result=[]):
if now == None:
return result
intermediateTraversal(now.left, result)
result.append(now.data)
intermediateTraversal(now.right, result)
return result
print(intermediateTraversal(binaryTree))
# 执行结果:[3, 1, 4, 0, 5, 2, 6]
11、不额外增加内存实现对数组的翻转,不能使用python内置方法(sorted(reverse=True),[::-1])
language = ['java', 'c语言', 'python']
for index, val in enumerate(language):
if index <= len(language)//2:
temp = language[-index-1]
language[-index - 1] = val
language[index] = temp
print(language)
-
python名次 1 优点:简单上手快 , java名次 2 优点:稳定,用者多,市场大 , c语言名次 3 优点:编程的基础
language = ['java', 'c语言', 'python'] ranking = (1,3,2) advantage = ({'优点':'简单好上手',}, {'优点':'编程的基础'},{'优点': '用者多,市场大'})题解
# 1.请按名次升序排列语言,以字典的形式展示; ranking = list(ranking) ranking[0],ranking[2] = ranking[2],ranking[0] # print(ranking) dict_language = dict(zip(ranking,language)) print({k:dict_language[k] for k in (sorted(dict_language.keys()))}) ''' {1: 'python', 2: 'java', 3: 'c语言'} '''# 2.请按名次降序排列优点,以字典的形式展示; dict_advantage = dict(zip(ranking,advantage)) print({k:dict_advantage[k] for k in (sorted(dict_advantage.keys(),reverse=True))})- 给定无序正整数数组,线性时间内找出第K大的值。
无序正整数数组 = [3,4,4,5,5,61,1,2,2,3,3,3,3,6,7,7,7,7,8,9]
解题思路:去重,用线性算法(归并排序和桶排序)排序,取出第K大的值。 参考博客:算法与数据结构
-
list1 = ['a','b','c'],list2 = [1,2,3],以list1的元素为键,以list2的元素为值,生成一个字典,并按照从键小到大的顺序排序
list_key = ['a','b','c']
list_value = [1,2,3]
dict1 = {k:v for k,v in sorted(zip(list_key,list_value),reverse=True)}
print(dict1)
- 求斐波那契数列第n项的值。
# 方式1:简单递归
def fib(n):
if n < 2:
return n
else:
return fib(n-1) + fib(n-2)
if __name == "__main__":
result = fib(100) # 你等到天荒地老,他还没有执行完
# 如上所示,代码简单易懂,然而这代码却极其低效。先不说这种递归的方式造成栈空间极大浪费,就仅仅是该算法的时间复杂度已经属于O(2^n)了。指数级别时间复杂度的算法跟不能用没啥区别!
# 方式2:
def fib(n):
results - list(range(n+1)) # 用于缓存以往结果,以便复用(目标2)
for i in range(n+1): # 按照顺序从小往大算(目标2)
if i < 2:
results[i] = i
else:
# 使用状态转移方程(目标1), 同时复用以往结果(目标2)
results[i] = results[i-1] + results[i-2]
return results[-1]
if __name == "__main__":
result = fib(100) # 秒算
15.一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为“Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为“Finish”)。
问总共有多少条不同的路径?
例如,上图是一个7 x 3 的网格。有多少可能的路径?
解这题,如前所述,我们需要完成三个子目标
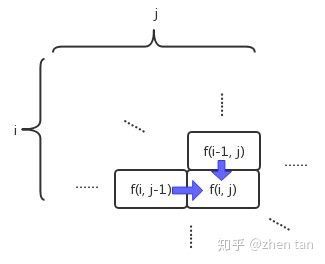
- 建立状态转移方程。该题就难在这里,这一步搞不定基本上就GG了。实际上,如图3所示,第i行第j列的格子的路径数,是等于它左边格子和上面格子的路径数之和:
2.缓存并复用以往结果。与之前说的一堆数列不同,这里的中间结果可以构成一个二维数列(如上图),所以需要用二维的数组或者列表来存储。
3.按顺序从小往大算。这次有两个维度,所以需两个循环,分别逐行和逐列让问题从小规模到大规模计算。
代码实现:
# m是行数,n是列数
def count_paths(m,n):
results = [[1]*n]*m # 将二维列表初始化为1,以便之后用于缓存(目标2)
# 题外话:results的空间复杂度不是O(nm),是O(n)
# 第0行和第0列的格子路径数显然均取值为1,所以跳过
for i in range(1,m): # 外循环逐行集散(目标3)
for j in range(1,n): # 内循环逐行计算(目标3)
# 状态方程(目标1),以及中间结果复用(目标2)
results[i][j] = results[i-1][j] + results[i][j-i]
return results[-1][-1]
if __name == "__main__":
result = count_paths(7,3) # 结果为28
- 把一元的钞票换成一分、二分、五分的硬币(每种至少一枚),问有多少种兑换方法。(请用伪代码或擅长语言进行逻辑实现)
# 方式一:暴力破解法
n=int(input())
cnt=0
for fen5 in range(n//5,0,-1):
for fen2 in range(n//2,0,-1):
for fen1 in range(n,0,-1):
if (fen5 * 5+fen2 * 2+fen1 == n):
print('fen5:{:d}, fen2:{:d}, fen1:{:d}, total:{:d}'.format(fen5, fen2, fen1, fen1+fen2+fen5))
cnt=cnt+1
print('count = {:d}'.format(cnt))
# 方式二:
count = 0
x = int(input()) #x∈(8,100)
a = x // 5
for m in range(a,0,-1): #fen5
b = (x - (m * 5)) // 2
for n in range(b,0,-1): #fen2
c = x - (5 * m) - (2 * n) #fen1
if m > 0 and n > 0 and c > 0: #每种硬币至少有一枚
print("fen5:{}, fen2:{}, fen1:{}, total:{}".format(m,n,c,m + n + c))
count += 1
print("count = {}".format(count))