抛出问题
给定\(N\)个数(\(int\)范围内),一共\(M\)次询问,每次都要询问区间\([l,r]\)的第\(k\)大的数。
其中\(N,M,l,r\)均不超过\(2\times 10^5\),保证询问有答案。
点我去模板题
解决问题
暴力法
显而易见,最暴力的办法就是区间排序然后输出排序后第\(k\)个数。最坏情况的时间复杂度是\(O(nm\lg n)\),不超时才怪。
主席树(可持久化线段树)法
于是针对这个问题,新的数据结构诞生了,也就是主席树。
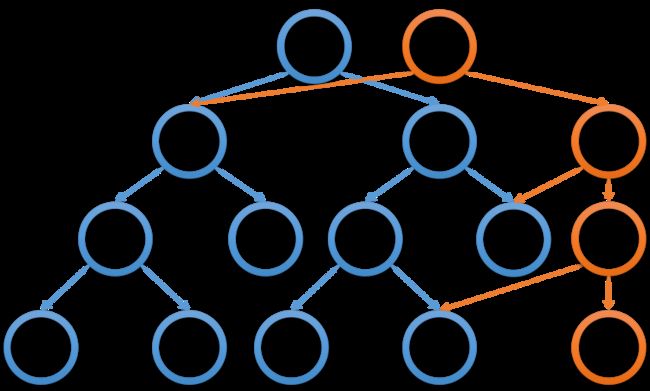
主席树本名可持久化线段树,也就是说,主席树是基于线段树发展而来的一种数据结构。其前缀"可持久化"意在给线段树增加一些历史点来维护历史数据,使得我们能在较短时间内查询历史数据,图示如下。
图中的橙色节点为历史节点,其右边多出来的节点是新节点(修改节点)。
下面我们来讲怎么构建这个数据结构。
主席树教程
- 要求:掌握线段树这个数据结构。
- 注意:一般主席树一类的题目,难的不是写主席树,而是主席树的运用。
主席树的点修改
不同于普通线段树的是主席树的左右子树节点编号并不能够用计算得到,所以我们需要记录下来,但是对应的区间还是没问题的。
//节点o表示区间[l,r],修改点为p,修改值根据题意设定(此处我们先不谈题目,只谈数据结构)
int modify(int o, int l, int r, int p)
{
int oo = ++node_cnt;
lc[oo] = lc[o]; rc[oo] = rc[o]; sum[oo] = sum[o] + 1;//新节点,这里是根据模板题来的
if(l == r)//递归底层返回新节点编号,修改父节点的儿子指向
{
//sum[oo] = t;如果题目要求sum是加t的再这样弄,然后上面的+1就去掉
return oo;
}
int mid = (l + r) >> 1;
if(p <= mid) lc[oo] = modify(lc[oo], l, mid);
else rc[oo] = modify(rc[oo], mid+1, r);
//sum[oo] = sum[lc[oo]] + sum[rc[oo]];在该题中,不需要这样做,但是很多情况下是要这样更新的
return oo;
}至于主席树的区间修改,其实也不难,但是复杂度有点高,简单点的题目一般只有点修改,有时候区间修改可以转化为点修改(比如NOIP2012借教室,有区间修改的解法也有点修改的解法)。
主席树的询问(历史区间和)
int ql, qr;//查询区间[l,r]
int query(int o, int l, int r)//节点o代表区间[l,r]
{
int ans = 0, mid = ((l + r) >> 1);
if(!o) return 0;//不存在的子树
if(ql <= l && r <= qr) return sum[o];//区间包含返回区间值
//都是线段树标准操作,只不过是左右子树多了一个记录而已
if(ql <= mid) ans += query(lc[o], l, mid);
if(qr > mid) ans += query(rc[o], mid+1, r);
return ans;
//点操作就不用说了
}主席树复杂度分析
如果只按照上述做法去做的话,每次修改的时间复杂度是\(O(\lg n)\),每次询问的复杂度也是\(O(\lg n)\)。
模板题教程
模板题就是主席树的典型例题,询问区间第\(k\)大。先不说区间\([l,r]\)吧,就说说\([1,r]\)怎么做。
模板题的[1,r]情况
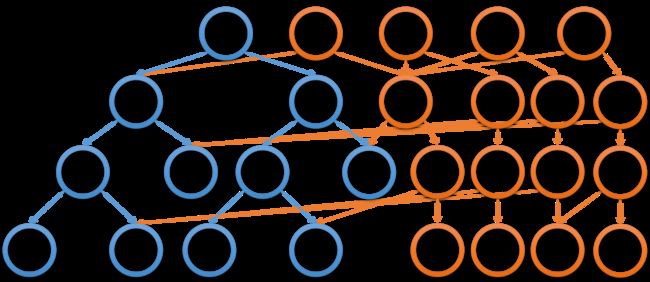
由题意知道我们肯定要对区间进行排序,但是我们的排序不是每次询问才排序,是初始化就排序离散化——针对数字较大但数据较小的情况(具体见方法)。排序离散化完毕后,以离散化数组建主席树,设\(i\)属于区间\([1,n]\),对原数组的\([1,i]\)区间的数做统计(例如下图,区间中按离散化数组顺序统计\(1\)的个数、\(2\)的个数、\(3\)的个数、\(4\)的个数、\(8\)的个数、\(9\)的个数),有序地插入节点到离散化数组的主席树中,记录好原数组每个节点对应的线段树起点,针对样例有几个示意图。注意,这里的橙色节点是新节点,与之前出现的那个图不一样。
我们按照上面的做法构建的主席树是为了方便我们查找第\(k\)小值。因为我们是以离散数组构建的主席树,那么从根节点出发,左子树部分的数必定不大于右子树部分的数。于是就可以将左儿子的节点个数\(x\)与\(k\)做比较,若\(k\leq x\),则第\(k\)小值一定在左子树里面,若\(x\leq k\),则第\(k\)小值一定在右子树里面,然后递归往下走,缩小范围。值得注意的是,前者递归时,\(k\)直接传下去即可,后者递归时,需要将\(k\)减去左子树的数的个数再传递这个\(k\)值。
例如我们查找\([1,4]\)中第\(2\)小的值,图示如下,绿色节点为该值存在的区间位置。
需要注意的是,第二个绿色节点才是绿色根节点的左子树,因为左子树表示的区间是靠前的那一半。
方法总结如下:
- 将原始数组复制一份,然后排序好,然后去掉多余的数,即将数据离散化。推荐使用C++的STL中的
unique函数; - 以离散化数组为基础,建一个全\(0\)的线段树,称作基础主席树;
- 对原数据中每一个\([1,i]\)区间统计,有序地插入新节点(题目中\(i\)每增加\(1\)就会多一个数,仅需对主席树对应的节点增加\(1\)即可);
- 对于查询\([1,r]\)中第\(k\)小值的操作,找到\([1,r]\)对应的根节点,我们按照线段树的方法操作即可(这个根节点及其子孙构成的必定是一颗线段树)。
模板题的解决
现在我们真正来解决区间询问\([l,r]\)的问题。
构建主席树的方法是没有问题的,问题正在于区间询问怎么写。其实,解决方案就是将主席树\([1,r]\)减去主席树\([1,l-1]\)就行了。其实这个原因并不难想,首先看到主席树的底层,全部是对数的统计。当主席树\([1,r]\)减去主席树\([1,l-1]\)时,统计也跟着减了,也就是说,现在统计记录的是\([l,r]\)区间。
而我们不需要单独减,只需要边递归查询边减,具体见查询部分代码。
//初始的u和v分别代表的是点l-1和点r,l和r分别表示线段树点代表的区间,初始的k如题
int query(int u, int v, int l, int r, int k)
{
int ans, mid = ((l + r) >> 1), x = sum[lc[v]] - sum[lc[u]];
//因为主席树是区间统计好了的,只要减一下即可,无需递归到叶子再处理
if(l == r)//找到目标位置
return l;
if(x >= k) ans = query(lc[u], lc[v], l, mid, k);
else ans = query(rc[u], rc[v], mid+1, r, k-x);//右子树记得改变k的值
return ans;
}模板题完整代码
至此,模板题也就解决了,下面是完整代码。注意,修改点定义为了全局变量。
#include
#include
#define M 200010
using namespace std;
int node_cnt, n, m;
int sum[M<<5], rt[M], lc[M<<5], rc[M<<5];//线段树相关
int a[M], b[M];//原序列和离散序列
int p;//修改点
void build(int &t, int l, int r)
{
t = ++node_cnt;
if(l == r)
return;
int mid = (l + r) >> 1;
build(lc[t], l, mid);
build(rc[t], mid+1, r);
}
int modify(int o, int l, int r)
{
int oo = ++node_cnt;
lc[oo] = lc[o]; rc[oo] = rc[o]; sum[oo] = sum[o] + 1;
if(l == r)
return oo;
int mid = (l + r) >> 1;
if(p <= mid) lc[oo] = modify(lc[oo], l, mid);
else rc[oo] = modify(rc[oo], mid+1, r);
return oo;
}
int query(int u, int v, int l, int r, int k)
{
int ans, mid = ((l + r) >> 1), x = sum[lc[v]] - sum[lc[u]];
if(l == r)
return l;
if(x >= k) ans = query(lc[u], lc[v], l, mid, k);
else ans = query(rc[u], rc[v], mid+1, r, k-x);
return ans;
}
int main()
{
int l, r, k, q, ans;
scanf("%d%d", &n, &m);
for(register int i = 1; i <= n; i += 1)
scanf("%d", &a[i]), b[i] = a[i];
sort(b+1, b+n+1);
q = unique(b+1, b+n+1) - b - 1;
build(rt[0], 1, q);
for(register int i = 1; i <= n; i += 1)
{
p = lower_bound(b+1, b+q+1, a[i])-b;//可以视为查找最小下标的匹配值,核心算法是二分查找
rt[i] = modify(rt[i-1], 1, q);
}
while(m--)
{
scanf("%d%d%d", &l, &r, &k);
ans = query(rt[l-1], rt[r], 1, q, k);
printf("%d\n", b[ans]);
}
return 0;
} 题目复杂度分析
题目一开始的离散化复杂度为\(O(n\lg n)\),构建基础主席树复杂度为\(O(n\lg n)\),统计并插入的复杂度是\(O(n\lg n + n\lg n)=O(n\lg n)\),询问的复杂度是\(O(m\lg n)\)。复杂度总和就是\(O((m+n)\lg n)\)。
尾注
至今还不知道为什么叫主席树。。。
这道题目是离线的,也就是使用的静态主席树。在线修改的一类题目也不难,在此不作讲解,但是以后可能会另写博客。
主席树这个数据结构还是非常棒的,这也提醒我们应该学会创造性思维。
- 感谢LMH大佬的帮助;
- 感谢洛谷平台的帮助;
- 感谢那些写题解的大佬的帮助。
写在最后
感谢大家的关注和阅读。
本文章借鉴了少许思路,最后经过本人思考独立撰写此文章,如需转载,请注明出处。