自适应稳定快速RLS算法---（SFTRLS算法）

在上一篇的博客文章中(浅谈自适应滤波器—（快速RLS算法）)，我给出了关于RLS的快速算法（简称FTRLS），但是它有一个缺点就是不够稳定，虽然我给出的例子里是稳定的，这主要是Matlab默认的计算精度是double型的，非常的高，所以没有出现问题。后来我在C6678 DSP用C语言实现该算法的时候使用的是float型的，得到的结果较Matlab的要差一些。

---

不稳定性分析

针对这种不稳定问题，一些研究人员对此进行了分析，研究发现不稳定的原因就是该算法内部存在正反馈的机制（可以类比电子电路当中的正反馈）。基于这种解释产生了如下思想，即如果能够得到数值误差的具体测量值，则可以通过其反馈使负反馈在误差传播中起主要的作用（这就好比通过引入合适的反馈网络使一个不稳定的放大电路变得稳定）。
具体的办法就是找出计算误差大的量，然后通过不同的公式来计算该量，因为在有限精度实现中，利用不同公式计算得到的结果是有差异的，而它们的差值可以很好的度量该参量的累计误差。然后可以将该误差进行反馈以便使算法稳定。那么现在的问题就是需要确定哪一个参量引入计算冗余度才能使误差传播变得稳定。在早期提出的解决方法中，只选择对一个参量引入冗余度。后来，人们发现至少需要两个参量才能保证FTRLS算法的稳定性。另一个相关问题是，在算法中应该使误差反馈到何处？一种自然的选择，是将误差反馈到与之相关的参量表达式中。这意味着对于每个引入冗余的参量，其最终值是用两种形式的组合来计算得到的。
在文献(D.T.M. Slock, T. Kailath, Numerically stable fast transversal filters for recursive least squares adaptive filtering. IEEE Tran. Signal Process. 39, 92-113(1991))中，提出了一种方法使得FTRLS算法得以稳定。其通过在γ(k,N)和e_b (k,N)中引入冗余来修正非稳定模式。这些量可以利用不同关系式来计算，为了加以区别，在其描述中增加了一个额外标志。
先验后向误差可以采用不同的形式进行描述，比如

和

其中，FTRLS算法采用了第一种形式，第二种形式对应于先验后向误差的内积实现。第三种是前面两种形式的线性组合，将这两种形式之间的数值差值进行反馈，以便确定出e_(b,i) (k,N,3)的最终值，这个值在稳定算法中的不同位置将会用到。对于每一个k_i，i = 1，2，3，选择不同的值，以保证相关特征值小于1。
转换因子γ(k,N)可能是第一个呈现出算法非稳定特性的参数。该参数也可以利用不用关系式计算出来，要求这些关系能够保证误差传播系统的所有模式都是稳定的。第一个关系式为

其中，ϕ_0 (k,N+1)是ϕ(k,N+1)的第一个元素。转换因子的第二个表达式为

第三个表达式为

计算出来的γ(k,N+1,1)通过下式作用到整个算法中。

利用转换因子和具有冗余的先验后向误差的各种表达式，我们就可以得到稳定快速横向RLS算法(SFTRLS)，下面给出了完整的算法描述

通过对比我在上一篇博客中给出了FTRLS算法，可以知道SFTRLS算法乘法量级为9N，而FTRLS为7N，计算量有所增加，这是由于加入的冗余计算导致的。

---

Matlab仿真

首先还是给出m代码

%FTF快速横向滤波算法
clc;
clear all;
close all;
%************************生成仿真信号**************************************
Fs = 10000;                                                     %设置采样频率
t = 0:1/Fs:3.5;  
t = t';
Size_t = size(t,1);
F1 = 2;
F2 = 10;
F3 = 20;
F4 = 1000;
Signal = sin(2*pi*F1*t) + 0.5*sin(2*pi*F2*t) + 0.25*sin(2*pi*F3*t); %生成信号
noise_amp = 1;                                           %定义噪声的标准差
noise1 = noise_amp*randn(Size_t,1);                        %生成高斯白噪声
noise2 = noise_amp*randn(Size_t,1);
noise3 = 5*sin(2*pi*F4*t);

noise = noise2;
Signal_noise = Signal + 0.2*noise;                           %加入高斯白噪声
Signal_noise(2:end) = Signal_noise(2:end) + 0.15*noise(1:end-1);
Signal_noise(3:end) = Signal_noise(3:end) + 0.1*noise(1:end-2);

subplot(2,1,1);
plot(t,Signal);
title('原始信号');
subplot(2,1,2);
plot(t,Signal_noise);
title('加入干扰噪声的信号');
%*************************************************************************
N = 3;                     %定义FIR滤波器阶数
Signal_Len = Size_t;       %定义信号数据的个数
lambda = 1.0001;                %定义遗忘因子1-0.4/(N+1)
delta = 0.01;    
y_out = zeros(Signal_Len,1);
Eta_out = zeros(Signal_Len,1);
w_out = zeros(Signal_Len,N);
for i = 1:Signal_Len
    %初始化数值
    if i==1
        w_f_last = zeros(N,1);
        w_b_last = zeros(N,1);
        w_last = zeros(N,1);
        Phi_last = zeros(N,1);
        gamma_last_3 = 1;
        xi_f_last = delta;
        xi_b_last = delta;
        k1 = 1.5;
        k2 = 2.5;
        k3 = 1;
        x_N_1 = zeros(N+1,1);
    end

    %输入数据
    if i<= N
        x_N_1(1:i) = noise(i:-1:1,1);
    else        
        x_N_1 = noise(i:-1:(i-N),1);
    end    
    d = Signal_noise(i);

    %算法主体
    e_f = x_N_1' * [1;-w_f_last];                                            %(1)(1)
    epsilon_f = e_f * gamma_last_3;                                          %(2)(2)
    Phi_N_1 = [0;Phi_last] + e_f/(lambda * xi_f_last)*[1;-w_f_last];         %(3)(5)
    Phi_N_1_0 = Phi_N_1(1);
    Phi_N_1_N_1 = Phi_N_1(end);
    gamma_N_1_1 = 1/(1/gamma_last_3 + Phi_N_1_0 * e_f);                      %(4)
    xi_f = 1/(1/(lambda * xi_f_last) - gamma_N_1_1 * Phi_N_1_0 * Phi_N_1_0); %(5)
    w_f = w_f_last + Phi_last * epsilon_f;                                   %(6)(4)
    e_b_1 = lambda * xi_b_last * Phi_N_1_N_1;                                %(7)(7)
    e_b_2 = [-w_b_last',1] * x_N_1;                                          %(8)
    e_b_3_1 = e_b_2 * k1 + e_b_1 * (1-k1);                                   %(9)
    e_b_3_2 = e_b_2 * k2 + e_b_1 * (1-k2);
    e_b_3_3 = e_b_2 * k3 + e_b_1 * (1-k3);
    gamma_2 = 1/(1/gamma_N_1_1 - Phi_N_1_N_1 * e_b_3_3);                     %(10)
    epsilon_b_3_1 = e_b_3_1 * gamma_2;                                       %(11)
    epsilon_b_3_2 = e_b_3_2 * gamma_2;
    xi_b = lambda * xi_b_last + epsilon_b_3_2 * e_b_3_2;                     %(12)(10)
    Phi = Phi_N_1 - Phi_N_1_N_1 * [-w_b_last;1];                             %(13)(11)
    Phi = Phi(1:end-1); 
    w_b = w_b_last + Phi * epsilon_b_3_1;                                    %(14)(12)
    x = x_N_1(1:N);
    gamma_3 = 1/(1 + Phi' * x);                                              %(15)
    %联合过程估计
    y = w_last'* x;                                                  
    e = d - y;                                                               %(16)(13)
    epsilon = e * gamma_3;                                                   %(17)(14)
    w = w_last + Phi * epsilon;                                              %(18)(15)
    %变量更替
    xi_f_last = xi_f;
    w_f_last = w_f;
    gamma_last_3 = gamma_3;
    xi_b_last = xi_b;
    Phi_last = Phi;
    w_b_last = w_b;
    w_last = w;
    %滤波结果存储
    y_out(i) = y;
    Eta_out(i) = e;
    w_out(i,:) = w';
end
figure;
subplot(2,1,1);
plot(y_out);
title('滤波器输出');
subplot(2,1,2);
plot(Eta_out);
title('输出误差');

figure;
plot(t,w_out(:,1),'r',t,w_out(:,2),'b',t,w_out(:,3),'y');
title('自适应滤波器系数');

运行一下得到如下结果



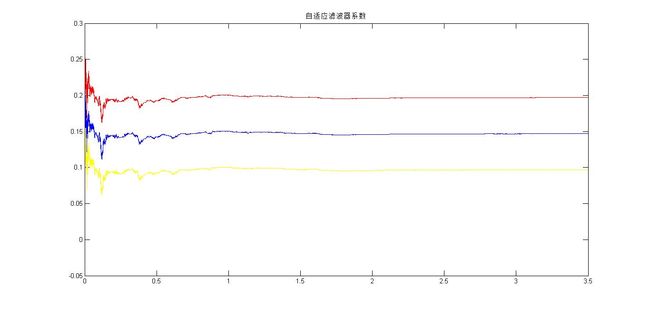
从运行得到的结果来看和FTRLS的差不多，在这里需要特别提醒一下的是初始化的时候一定要格外的小心，我刚开始把这个算法敲完后一运行，结果老是发散，我开始以为是哪个公式我搞错了，检查了半天也没有发现什么问题，后来在我吃饭的时候，突然灵光一闪，我才发现是输入的数据向量x(k,N+1)搞错了，原来在FTRLS上这么错误的初始化没有问题程序可以正常的运行，但是在SFTRLS上这样就不行了，究其原因是它增加了冗余计算，并且是靠误差来抑制正反馈，结果我在一开始就人为的引入了一个额外的误差，很快的就使Matlab浮点运算溢出了，怎么调节都调节不回来了。后来我改过来就好使了，也就是你们现在看到的程序。

---

在上一篇博客的最后我给大家说我准备用TMS320F2812来做一个声学回声消除的扩音系统，我趁着这个中秋研究了一下，发现我的那个板子上的DAC更新速度太慢了只能达到100KHz，ADC还好可以达到1MHz，但是如果以40KHz（语音信号的有效频带为400Hz~4KHz）为调节频率的话，每个调节周期（25us）大概有一半的时间是在采集数据和输出数据，还有一半的时间用来计算，2812是定点的DSP没有浮点运算单元，主频为150MHz，像这种情况需要的FIR滤波器阶数至少是几百阶，也就是说当采用最简单的LMS算法，每次要进行几百次的浮点运算，这个时间已经超出了12.5us，所以用2812已经是行不通了。
但是这个声学回声消除扩音系统还是要做的，我手上现在正好有TMS320C6678，它是一个八核浮点DSP用它是搓搓有余了，不过我得自己画板子外挂高速的ADC和DAC，也罢正好我用C语言写的LMS算法、FTRLS算法、SFTRLS算法都是在它上面验证的，本来想在硬件上偷个懒的，用2812省事一些，看来这个懒偷不成了，慢慢来吧，祝我好运。