深度学习——感知机（perceptron）图文详解

一，什么是感知机

感知机是由美国学者FrankRosenblatt在1957年提出来的。感知机是作为神经网络（深度学习）的起源的算法。因此，学习感知机的构造也就是学习通向神经网络和深度学习的一种重要思想。
感知机接收多个输入信号，输出一个信号。这里所说的“信号”可以想象成电流或河流那样具备“流动性”的东西。像电流流过导线，向前方输送电子一样，感知机的信号也会形成流，向前方输送信息。但是，和实际的电流不同的是，感知机的信号只有“流/不流”（1/0）两种取值。这里我们认为0对应“不传递信号”， 1对应“传递信号”。
下图1就是一个接收两个输入信号的感知机的例子。

图1 两个输入的感知机
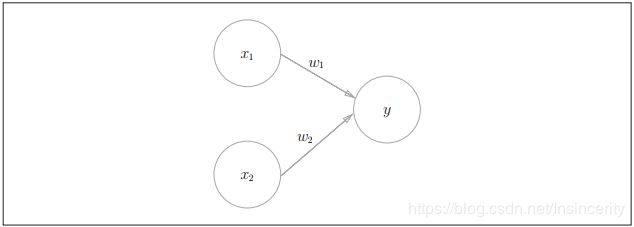
x1、 x2是输入信号，y是输出信号， w1、 w2是权重（w是weight的首字母）。图中的○称为“神经元”或者“节点”。输入信号被送往神经元时，会被分别乘以固定的权重（w1x1、 w2x2）。神经元会计算传送过来的信号的总和，只有当这个总和超过了某个界限值时，才会输出1。这也称为“神经元被激活” 。这里将这个界限值称为阈值，用符号θ表示。
感知机的运行原理只有这些！把上述内容用数学式来表示，就是下面这个式子（1）。
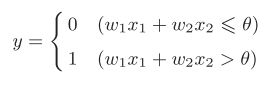感知机的多个输入信号都有各自固有的权重，这些权重发挥着控制各个信号的重要性的作用。也就是说，权重越大，对应该权重的信号的重要性就越高。

二，用感知机搭建简单逻辑电路

2.1 与门

知道了上面那些概念，那如何用感知机来解决简单的问题呢？这里首先以逻辑电路为题材来思考一下与门（AND gate）。与门是有两个输入和一个输出的门电路。下图这种输入信号和输出信号的对应表称为“真值表”。如图所示，与门仅在两个输入均为1时输出1，其他时候则输出0。

图2 与门真值表
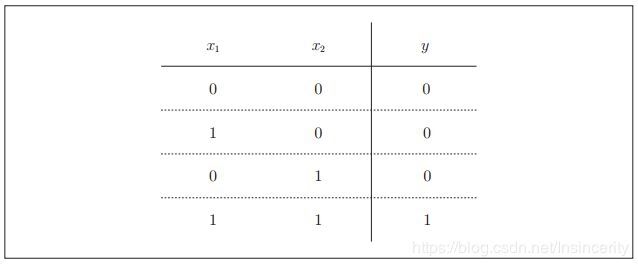
下面考虑用感知机来表示这个与门。需要做的就是确定能满足图中的真值表的w1、 w2、 θ的值。那么，设定什么样的值才能制作出满足图中条件的感知机呢？实际上，满足上图条件的参数选择方法有无数多个。比如，当(w1, w2, θ) = (0.5, 0.5, 0.7) 时，可以满足图中条件。此外，当 (w1, w2, θ)为(0.5, 0.5, 0.8)或者(1.0, 1.0, 1.0)时，同样也满足与门的条件。设定这样的参数后，仅当x1和x2同时为1时，信号的加权总和才会超过给定的阈值θ。

2.2 与非门，或门

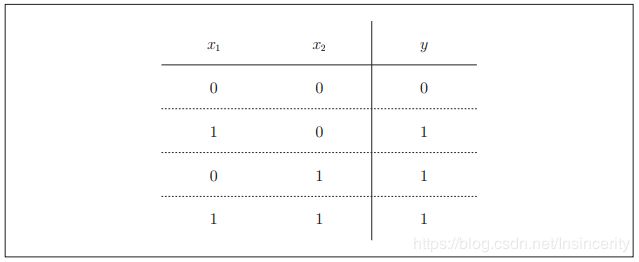
接着，我们再来考虑一下与非门（NAND gate）。NAND是Not AND的意思，与非门就是颠倒了与门的输出。用真值表表示的话，如下图所示，仅当x1和x2同时为1时输出0，其他时候则输出1。？

图3 与非门真值表
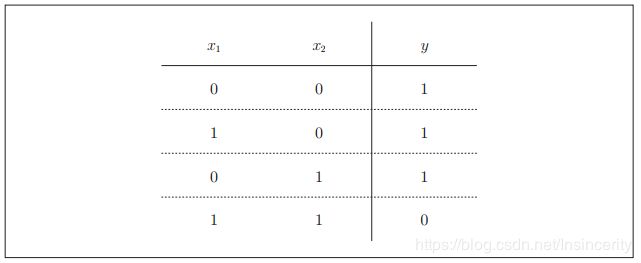
要表示与非门，可以用(w1, w2, θ) = (−0.5, −0.5, −0.7)这样的组合（其他的组合也是无限存在的）。实际上，只要把实现与门的参数值的符号取反，就可以实现与非门。接下来咱们再来看一下下面这张图所示的或门。或门是“只要有一个输入信号是1，输出就为1”的逻辑电路。
图4 或门真值表
注意：这里决定感知机参数的并不是计算机，而是我们人。我们看着真值表这种“训练数据”，人工考虑（想到）了参数的值。而机器学习的课题就是将这个决定参数值的工作交由计算机自动进行。 学习是确定合适的参数的过程，而人要做的是思考感知机的构造（模型），并把训练数据交给计算机。
如上所示，我们已经知道使用感知机可以表示与门、与非门、或门的逻辑电路。这里重要的一点是：与门、与非门、或门的感知机构造是一样的。实际上， 3个门电路只有参数的值（权重和阈值）不同。也就是说，相同构造的感知机，只需通过适当地调整参数的值，就可以像“变色龙演员”表演不同的角色一样，变身为与门、与非门、或门。

三，感知机的实现

3.1 简单感知机的实现

我们用Python来实现刚才的逻辑电路。这里，先定义一个接收参数x1和x2的AND函数。

def AND(x1, x2):
	w1, w2, theta = 0.5, 0.5, 0.7
	tmp = x1*w1 + x2*w2
	if tmp <= theta:
		return 0
	elif tmp > theta:
		return 1

在函数内初始化参数w1、 w2、 theta，当输入的加权总和超过阈值时返回1，否则返回0。我们来确认一下输出结果是否如图2 与门真值表所示。

AND(0, 0) # 输出0
AND(1, 0) # 输出0
AND(0, 1) # 输出0
AND(1, 1) # 输出1

和我们预想的输出一样，这样我们就实现了与门。按照同样的步骤，也可以实现与非门和或门。

3.2 导入权重和偏置

下面让我们来对上面的简单感知机的实现稍作修改。刚才与门的实现比较直接、容易理解，但是考虑到以后的事情，我们将其修改为另外一种实现形式。在此之前，首先把式子（1）的θ换成−b，于是就可以用式（2）来表示感知机的行为了。

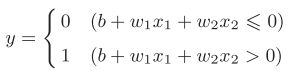
式（1）和式（2）虽然有一个符号不同，但表达的内容是完全相同的。此处， b称为偏置， w1和w2称为权重。如式（2）所示，感知机会计算输入信号和权重的乘积，然后加上偏置，如果这个值大于0则输出1，否则输出0。下面，我们使用NumPy，按式（2）的方式实现感知机。在这个过程中，我们用Python的解释器逐一确认结果。

>>> import numpy as np
>>> x = np.array([0, 1]) # 输入
>>> w = np.array([0.5, 0.5]) # 权重
>>> b = -0.7 # 偏置
>>> w*x
array([ 0. , 0.5])
>>> np.sum(w*x)
0.5
>>> np.sum(w*x) + b
-0.19999999999999996 # 大约为-0.2（由浮点小数造成的运算误差）

如上例所示，在NumPy数组的乘法运算中，当两个数组的元素个数相同时，各个元素分别相乘，因此w*x的结果就是它们的各个元素分别相乘（[0, 1] [0.5, 0.5] => [0, 0.5]）。之后， np.sum(wx)再计算相乘后的各个元素的总和。最后再把偏置加到这个加权总和上，就完成了式（2）的计算。

3.3 使用权重和偏置的实现

使用权重和偏置，可以像下面这样实现与门。

def AND(x1, x2):
	x = np.array([x1, x2])
	w = np.array([0.5, 0.5])
	b = -0.7
	tmp = np.sum(w*x) + b
	if tmp <= 0:
		return 0
	else:
		return 1

这里把−θ命名为偏置b，但是请注意，偏置和权重w1、 w2的作用是不一样的。具体地说， w1和w2是控制输入信号的重要性的参数，而偏置是调整神经元被激活的容易程度（输出信号为1的程度）的参数。比如，若b为−0.1，则只要输入信号的加权总和超过0.1，神经元就会被激活。但是如果b为−20.0，则输入信号的加权总和必须超过20.0，神经元才会被激活。像这样，偏置的值决定了神经元被激活的容易程度。另外，这里我们将w1和w2称为权重，将b称为偏置，但是根据上下文，有时也会将b、 w1、 w2这些参数统称为权重。（实际上，在式(2) 的b + w1x1 + w2x2的计算中，当输入x1和x2为0时，只输出偏置的值。）
接着，我们继续实现与非门和或门。

def NAND(x1, x2):
	x = np.array([x1, x2])
	w = np.array([-0.5, -0.5]) # 仅权重和偏置与AND不同！
	b = 0.7
	tmp = np.sum(w*x) + b
	if tmp <= 0:
		return 0
	else:
		return 1
		
def OR(x1, x2):
	x = np.array([x1, x2])
	w = np.array([0.5, 0.5]) # 仅权重和偏置与AND不同！
	b = -0.2
	tmp = np.sum(w*x) + b
	if tmp <= 0:
		return 0
	else:
		return 1

我们在前面已经介绍过，与门、与非门、或门是具有相同构造的感知机，区别只在于权重参数的值。因此，在与非门和或门的实现中，仅设置权重和偏置的值这一点和与门的实现不同。

四，感知机的局限性

到这里我们已经知道了，使用感知机可以实现与门、与非门、或门三种逻辑电路。但现在我们来考虑一下异或门（XOR gate）吧。

4.1 异或门

异或门也被称为逻辑异或电路。如图2-5所示，仅当x1或x2中的一方为1时，才会输出1（“异或”是拒绝其他的意思）。那么，要用感知机实现这个异或门的话，应该怎么设定权重参数呢？

图5 异或门真值表
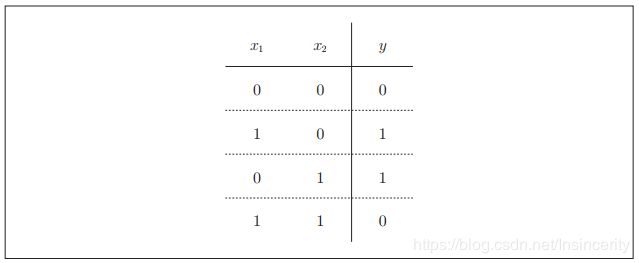
实际上，用前面介绍的感知机是无法实现这个异或门的。为什么用感知机可以实现与门、或门，却无法实现异或门呢？下面我们尝试通过画图来思考其中的原因。
首先，我们试着将或门的动作形象化。或门的情况下，当权重参数(b, w1, w2) = (−0.5, 1.0, 1.0)时，可以满足图4 或门真值表条件。此时，感知机可用下面的式（3）表示。

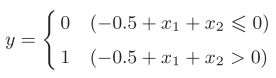
式（3）表示的感知机会生成由直线−0.5 + x1 + x2 = 0分割开的两个空间。其中一个空间输出1，另一个空间输出0，如图6所示
图6 感知机的可视化：灰色区域是感知机输出0的区域，这个区域与或门的性质一致
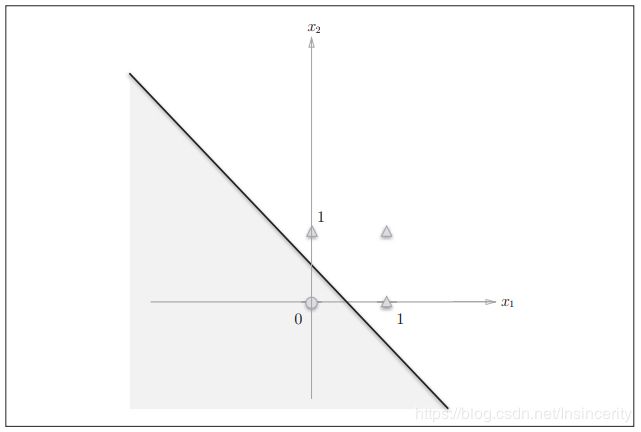
或门在(x1, x2) = (0, 0)时输出0，在(x1, x2)为(0, 1)、 (1, 0)、 (1, 1)时输出1。图6中，○表示0，△表示1。如果想制作或门，需要用直线将图6中的○和△分开。实际上，刚才的那条直线就将这4个点正确地分开了。那么，换成异或门的话会如何呢？能否像或门那样，用一条直线作出分割图7中的○和△的空间呢？
图7 ○和△表示异或门的输出
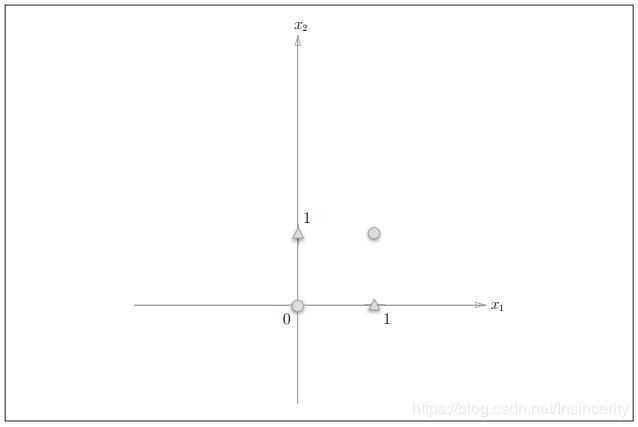
想要用一条直线将图7中的○和△分开，无论如何都做不到。事实上，用一条直线是无法将○和△分开的。

4.2 线性和非线性

图7中的○和△无法用一条直线分开，但是如果将“直线”这个限制条件去掉，就可以实现了。比如，我们可以像图8那样，作出分开○和△的空间。

图8 使用曲线可以分开○和△
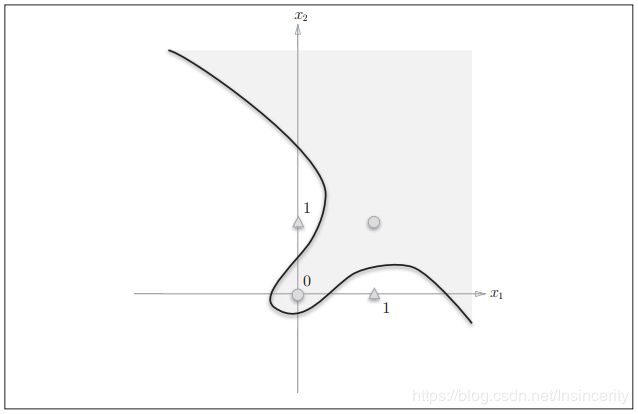
感知机的局限性就在于它只能表示由一条直线分割的空间。图8这样弯曲的曲线无法用感知机表示。另外，由图8这样的曲线分割而成的空间称为非线性空间，由直线分割而成的空间称为线性空间。线性、非线性这两个术语在机器学习领域很常见，可以将其想象成图6和图8所示的直线和曲线。

五，多层感知机

的确，感知机不能表示异或门，但也不用太失望，因为感知机还可以有“叠加层”（即可以通过叠加层来表示异或门）。这就是多层感知机，不过这个我们以后再继续做详细介绍了。

 

 

参考文献： 深度学习入门：基于Python的理论与实现Deep Learning from Scratch