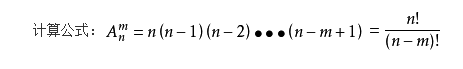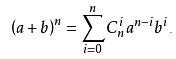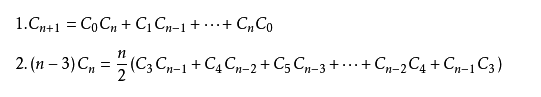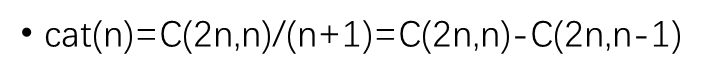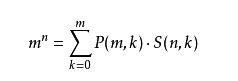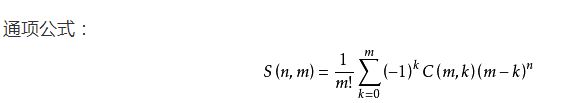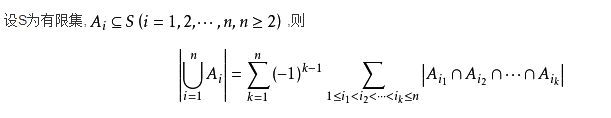CSP-S 2019初赛知识点总结之数学
数学有关
汉诺塔
设 f [ n ] [ m ] f[n][m] f[n][m] 表示 n n n 个盘子, m m m 个柱子的汉诺塔
当 m = 3 m=3 m=3 时, f [ n ] [ m ] = 2 n − 1 f[n][m]=2^{n}-1 f[n][m]=2n−1
当 m > 3 m>3 m>3 时, f [ n ] [ m ] = m i n 0 < = k < n 2 ∗ f [ k ] [ m ] + f [ n − k ] [ m − 1 ] f[n][m]=min_{0<=k
算术表达式
中缀表达式
最常见的表达式,如:3*(1 - 2)
前缀表达式
又称波兰式,如:* 3 - 1 2
后缀表达式
又称逆波兰式, 如:1 2 - 3 *
笛卡尔坐标系
是直角坐标系和斜坐标系的统称。
互相垂直且有公共原点的两条数轴构成平面直角坐标系,而如果坐标系中两条坐标轴不垂直,那么这样的坐标系称为“斜坐标系”。
哈密顿图
哈密顿通路(回路)与哈密顿图 (Hamilton图) 通过图G的每个结点一次,且仅一次的通路(回路),就是哈密顿通路(回路)。存在哈密顿回路的图就是哈密顿图。
与欧拉图的情形不同,到目前为止还未找到判断一个图是否是哈密顿图的非平凡的充要条件。
事实上这是图论中尚未解决的主要问题之一。
哈密顿图有很多充分条件,例如,
(1)若图的最小度不小于顶点数的一半,则图是哈密顿图;
(2)若图中每一对不相邻的顶点的度数之和不小于顶点数,则图是哈密顿图。
另外,还有很多用度序列、度和、图的坚韧度等参数给出的充分条件。
哈密顿图的充分条件和必要条件
定理1: 设无向图G是哈密顿图,V1是V的任意的非空子集, p(G-V1)≤|V1| 其中,p(G-V1)为从G中删除V1(删除V1中各顶点及关联的边)后所得到的图的连通分支。
定理2: 设G是n(n≥3)阶无向简单图,如果G中任何一对不相邻的顶点度数之和都大于等于n,则G是哈密顿图。
定理3: 在n(n≥2)阶有向图D=中,如果所有有向边均用无向边代替,所得无向图中含生成子图Kn,则有向图中存在哈密顿图。
推论: n(n≥3)阶有向完全图为哈密顿图。
哈密顿路径也称作哈密顿链,指在一个图中沿边访问每个顶点恰好一次的路径。寻找这样的一个路径是一个典型的NP-完全(NP-complete)问题。后来人们也证明了,找一条哈密顿路的近似比为常数的近似算法也是NP完全的。
一般地,寻找一个图的哈密顿圈问题是 NP 困难的
哈密顿图及其判定方法可以解决中国邮路问题、旅行售货员问题、排座位问题、判定图是否可一笔画问题。
排列组合
排列
从n个不同元素中,任取m(m≤n,m与n均为自然数,下同)个不同的元素按照一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列;
从n个不同元素中取出m(m≤n)个元素的所有排列的个数,叫做从n个不同元素中取出m个元素的排列数,用符号 A(n,m)表示。
规定0! = 1
组合
从n个不同元素中,任取m(m≤n)个元素并成一组,叫做从n个不同元素中取出m个元素的一个组合;
从n个不同元素中取出m(m≤n)个元素的所有组合的个数,叫做从n个不同元素中取出m个元素的组合数。用符号 C(n,m) 表示。
二项式定理
特殊优先
特殊元素,优先处理;特殊位置,优先考虑。
例:六人站成一排,求
⑴甲、乙既不在排头也不在排尾的排法数
⑵甲不在排头,乙不在排尾,且甲乙不相邻的排法数
分析:⑴按照先排出首位和末尾再排中间四位分步计数
第一步:排出首位和末尾、因为甲乙不在首位和末尾,那么首位和末尾实在其它四位数选出两位进行排列、一共有A(4,2)=12种;
第二步:由于六个元素中已经有两位排在首位和末尾,因此中间四位是把剩下的四位元素进行顺序排列,
共A(4,4)=24种;
根据乘法原理得即不再排头也不在排尾数共12×24=288种。
⑵第一类:甲在排尾,乙在排头,有A(4,4)种方法。
第二类:甲在排尾,乙不在排头,有3×A(4,4)种方法。
第三类:乙在排头,甲不在排尾,有3×A(4,4)种方法。
第四类:甲不在排尾也不在排头,乙不在排头也不在排尾,有6×A(4,4)种方法(排除相邻)。
共A(4,4)+3×A(4,4)+3×A(4,4)+6×A(4,4)=312种。
捆绑与插空
例:8人排成一队
⑴甲乙必须相邻
⑵甲乙不相邻
⑶甲乙必须相邻且与丙不相邻
⑷甲乙必须相邻,丙丁必须相邻
⑸甲乙不相邻,丙丁不相邻
分析:⑴甲乙必须相邻,就是把甲乙 捆绑(甲乙可交换) 和7人排列A(7,7)×A(2,2)
⑵甲乙不相邻,A(8,8)-A(7,7)×2。或A(6,6)×A(7,2)
⑶甲乙必须相邻且与丙不相邻,先求甲乙必须相邻且与丙相邻A(6,6)×2×2
甲乙必须相邻且与丙不相邻A(7,7)×2-A(6,6)×2×2
⑷甲乙必须相邻,丙丁必须相邻A(6,6)×2×2
⑸甲乙不相邻,丙丁不相邻,A(8,8)-A(7,7)×2×2+A(6,6)×2×2
卡特兰数
应用
1.括号序列:给出一个有n个运算符,n+1个运算数的算式,要求在算式中任意添加括号,那么本质不同的运算顺序有多少种?
2.有2n个人排队进入剧场,入场费50元,每个人都带着一张50元或100元,剧院售票处没有任何零钱,有多少种情况满足无论什么时候售票处都能找的开零钱
3.一个n*n的网格图,从左上走到右上,每次只能向上走或向右走,不能走到左下到右上的对角线的上方,一共有多少种走法?
4.有n个节点的形态不同的二叉树一共有多少棵?
5.出栈序列统计,有n个数和一个栈,本质不同的合法序列一共有多少种?
第二类斯特林数
表示将n个不同的元素分成m个集合的方案数。

第二类Stirling数的推导可以从定义出发考虑第n+1个元素的情况,假设要把n+1个元素分成K个集合则分析如下:
(1)如果n个元素构成了k-1个集合,那么第n+1个元素单独构成一个集合。方案数 S ( n − 1 , k ) S(n-1,k) S(n−1,k)。
(2)如果n个元素已经构成了k个集合,将第n+1个元素插入到任意一个集合。方案数 k ∗ S ( n , k ) k*S(n,k) k∗S(n,k) 。
应用
第二类Stirling数主要是用于解决组合数学中的几类放球模型。主要是针对于球之前有区别的放球模型:
(1)n个不同的球,放入m个无区别的盒子,不允许盒子为空。
方案数: S ( n , m ) S(n,m) S(n,m)。这个跟第二类Stirling数的定义一致。
(2)n个不同的球,放入m个有区别的盒子,不允许盒子为空。
方案数: m ! ⋅ S ( n , m m!·S(n,m m!⋅S(n,m) 。因盒子有区别,乘上盒子的排列即可。
(3)n个不同的球,放入m个无区别的盒子,允许盒子为空。
方案数: ∑ k = 0 m S ( n , k ) \sum_{k=0}^{m}S(n,k) ∑k=0mS(n,k) 。枚举非空盒的数目便可。
(4)n个不同的球,放入m个有区别的盒子,允许盒子为空。
①方案数: ∑ k = 0 m S ( n , k ) A ( m , k ) \sum_{k=0}^{m}S(n,k)A(m,k) ∑k=0mS(n,k)A(m,k)。同样可以枚举非空盒的数目,注意到盒子有区别,乘上一个排列系数。
②既然允许盒子为空,且盒子间有区别,那么对于每个球有m种选择,每个球相互独立。有方案数: m n m^{n} mn 。
容斥原理和错排公式
容斥原理
先不考虑重叠的情况,把包含于某内容中的所有对象的数目先计算出来,然后再把计数时重复计算的数目排斥出去,使得计算的结果既无遗漏又无重复,这种计数的方法称为容斥原理。
错排
考虑一个有n个元素的排列,若一个排列中所有的元素都不在自己原来的位置上,那么这样的排列就称为原排列的一个错排。 n个元素的错排数记为D(n)。
D n = n ! ( 1 − 1 1 ! + 1 2 ! − 1 3 ! + . . . + ( − 1 ) n ∗ 1 n ! ) D_{n}=n!(1- \frac{1}{1!} + \frac{1}{2!} - \frac{1}{3!}+...+(-1)^{n}*\frac{1}{n!}) Dn=n!(1−1!1+2!1−3!1+...+(−1)n∗n!1)
D n = ( n − 1 ) ∗ ( D n − 1 + D n − 2 ) D_{n}=(n-1)*(D_{n-1}+D_{n-2}) Dn=(n−1)∗(Dn−1+Dn−2)
鸽巢原理
假如有n+1个元素放到n个集合中去,其中必定有一个集合里至少有两个元素。
把多于mn(m乘n)+1(n不为0)个的物体放到n个抽屉里,则至少有一个抽屉里有不少于(m+1)的物体。
把无数还多件物体放入n个抽屉,则至少有一个抽屉里有无数个物体。
把(mn-1)个物体放入n个抽屉中,其中必有一个抽屉中至多有(m—1)个物体
博弈类问题
Nim取石子游戏
有一堆石子,共n个,两个人轮流取石子,每次最少取1个,最多取m个,取完最后一个石子的人获胜
当 n mod (m + 1)= 0 时,先手必败;否则先手必胜。必胜策略是每次都取走当前石子数 mod (m+1)的值
一个重要性质
从必败态走到的每一个状态都为必胜态,从必胜态操作一步走到的所有状态中至少有一个是必败态。规定无法操作的状态为必败态。
二分图
二分图又称作二部图,是图论中的一种特殊模型。 设G=(V,E)是一个无向图,如果顶点V可分割为两个互不相交的子集(A,B),并且图中的每条边(i,j)所关联的两个顶点i和j分别属于这两个不同的顶点集(i in A,j in B),则称图G为一个二分图。
充要条件:G至少有两个顶点,图中不含奇环
如果二分图的某一类点有x个,另一类点有y个,那么这个二分图中最多有xy条边