信号DOA估计

DOA估计（或波达方向估计）：将接受信号进行空间傅里叶变换（空间傅里叶变换和离散时间傅里叶变换的区别是，空间傅里叶变换的求和是对阵元空间位置m，而时域傅里叶变换的求和变量时离散时间n），进而取模的平方得到空间谱，估计出信号的到达方向（空间谱的最大值对应的相位φ，再根据定义φ=2πdsinθ/λ，计算θ）。

1、概念

• 假设均匀线阵，空间仅有一个信号源，则接受信号可以表示为：

                    

• 空间傅里叶变换则为：

                                       

2、方法

基于MUSIC算法的DOA估计（需要进行谱峰搜索，计算量大）

• 和功率谱估计一样，考虑有K个信号源，M个阵元，则阵列接受信号可以表示为：x(n)=As(n)+v(n)
• 求输入信号的相关矩阵R，利用信号子空间和噪声子空间的正交性原理，对R进行特征值分解，将最小的M-K的特征值对应的特征向量组成矩阵G，计算出MUSIC谱，进行谱峰搜索即可找到前K个φ，从而找到前K个θ。

                   

• 对于矩形阵：

           

基于ESPRIT算法的DOA估计

• 取前M-1个阵元A1和后M-1个阵元A2构成两个子阵来考虑；功率谱是y(n)=x(n+1)
• 算法原理首先考虑两个阵元方向矩阵的关系，A2=A1φ，φ是一个K*K对角阵，K个对角元与K个波达方向θ有关。于是就去找如何得出这个φ。
• 对接受信号计算相关矩阵R，对其进行特征值分解。构造信号子空间S和噪声子空间的矩阵G（特征向量构成）；
• 由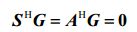得出S和A的列张成的是一个相同的子空间，所以就有线性变换S=AT；取S的前M-1行和后M-1行分别为S1和S2，则有：，所以S1的列,S2的列和方向矩阵A1的列张成相同的子空间，同样的写出线性变换S2=S1T，span{S2}=span{S1}就体现了旋转不变形，更具体的为，。
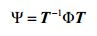• 由的表达式可以看出其与φ的特征值一样，所以只用求的特征值即可。

clc,clear all,close all
%% 产生信号样本
N=100;M=10;%信号样本数目和阵元个数
K=2;%信源个数
theta=[-10;40]*pi/180;
SNR=[10;20];sigma=1;
Am=sqrt(2*sigma^2*10.^(SNR/10));
% Am=[sqrt(10.^(SNR/10))];
S=Am*ones(1,N);
S(2,:)=S(2,:).*exp(1i*2*pi*rand(1,N));
for a=1:M
for b=1:K
A(a,b)=exp(-1i*(a-1)*pi*sin(theta(b)));%第 b 列对应的都是 theta(b)
end
end
V=zeros(M,N);
for m=1:M
v=wgn(1,N,0,'complex');
v=v-mean(v);
v=v/std(v);
V(m,:)=v;
end
X=A*S+V;
%% 利用接受数据估计信号的空间相关矩阵 R
R=zeros(M,M);
for i=1:N
R=R+X(:,i)*X(:,i)';
end
R=R/N;%是一个统计平均
%MUSIC 算法
[VR,D]=eig(R);
D=real(D);
[B,IX]=sort(diag(D));
G=VR(:,IX(M-K:-1:1));
MUSICP=[];
for n=-pi/2:pi/180:pi/2
a=exp(-1i*[0:M-1]'*pi*sin(n));
MUSICP=[MUSICP,1/(a'*G*G'*a)];
MUSICP=real(MUSICP);end
n=length(MUSICP);
maxx=max(MUSICP);
figure,plot(-90:1:90,10*log10((MUSICP+eps)/maxx)+3.5),axis([-90,90,-
60,inf]),title('MUSIC 算法')
%RootMUSIC 算法
syms z
pz=z.^([0:M-1]');
pz1=(z^(-1)).^([0:M-1]);
fz=z^(M-1)*pz1*G*G'*pz;
a=sym2poly(fz);
r=roots(a);
r1=abs(r);
for i=1:2*K %每个信号源有 K 个
[Y,I(i)]=min(abs(r1-1));
r1(I(i))=inf;
end
for i=1:2*K
theta_esti(i)=asin(-angle(r(I(i)))/pi)*180/pi;
end
%ESPRIT 算法
S=VR(:,IX(M:-1:M-K+1));
S1=S(1:M-1,:);
S2=S(2:M,:);
fai=S1\S2;
[U_fai,V_fai]=eig(fai);
for i=1:K
ESPRITtheta_esti(i)=asin(-angle(V_fai(i,i))/pi)*180/pi;
end
%MVDR 算法
MVDRP=[];
for n=-pi/2:pi/180:pi/2
a=exp(-1i*[0:M-1]'*pi*sin(n));
MVDRP=[MVDRP,1/(a'*inv(R)*a)];
end
n=length(MVDRP);
maxx=max(MVDRP);
figure,plot(-90:1:90,10*log10((MVDRP+eps)/maxx)+3.5),axis([-90,90,-
35,inf]),title('MVDR')
%F-SAPES 算法
P=6;%子阵数目L=M+1-P;%子阵阵元数目，书上是 M-1
Rf=zeros(L,L);
for i=1:P
Rf=Rf+X(i:i+L-1)*X(i:i+L-1)'/N;
end
Rf=Rf/P; %子阵平滑后的空间相关矩阵
n1=0:P-1;
n2=0:L-1;
cc=[1 zeros(1,L-1)];
for n3=-90:.5:90
fy=exp(1i*pi*sin(n3/180*pi));
tt=[(fy.^(n1')).' zeros(1,M-P)];
Tfy=toeplitz(cc,tt);
GfTheta=1./(P^2)*Tfy*R*Tfy';
Qf=Rf-GfTheta;
aTheta=fy.^(-n2');
Wof=(Qf\aTheta)./(aTheta'*(Qf\aTheta));
sigma2sTheta(((n3+90)/.5+1))=Wof'*GfTheta*Wof;
end
maxx=max(sigma2sTheta);
figure,plot(-90:.5:90,10*log10((sigma2sTheta+eps)/maxx)+3.5),axis([-90,90,-
35,inf]),title('F-SAPES')