离散卷积过程举例图示详解
卷积结果的通俗解释:
f(x)是待处理的信号。通常地,该函数数据个数比较多。
g(x)是对信号前后相关性的描述的函数。通常地,该函数非零数据个数比较少。它通常具有在(-∞,+∞)内可积且快速收敛的特性。
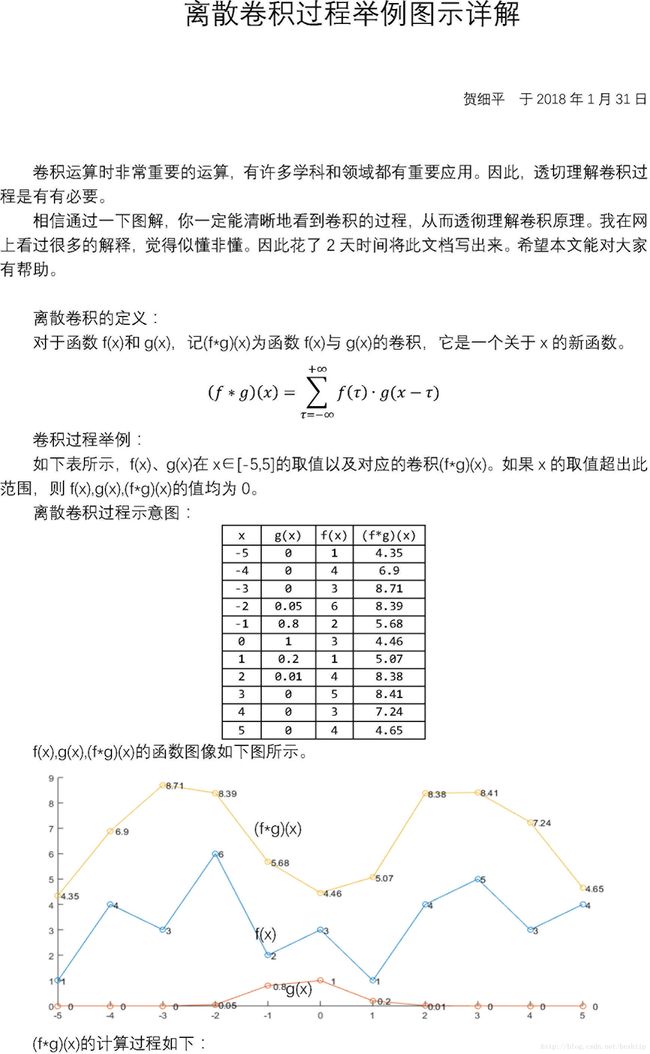
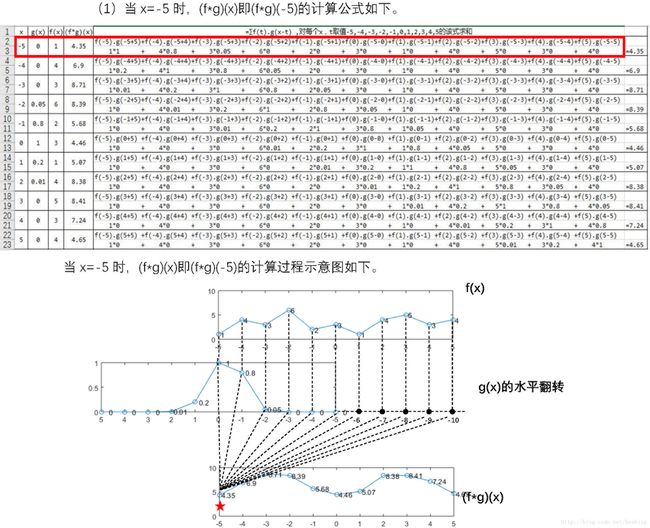
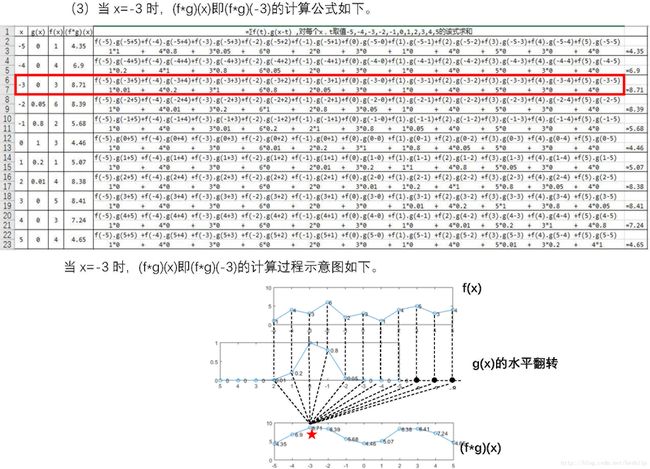
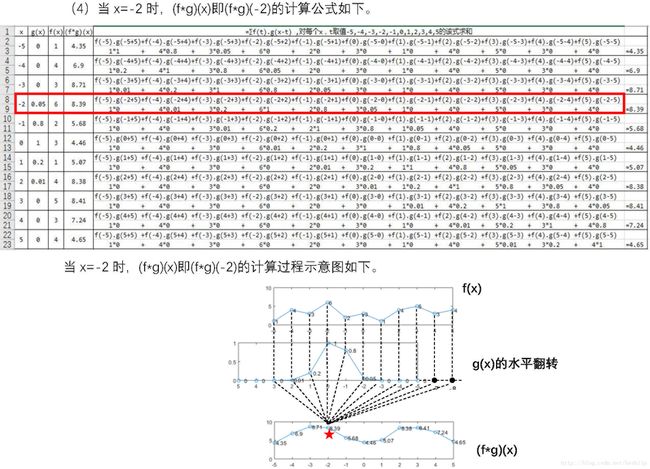
对于本例中的函数g(x),卷积的结果可以解释为:在x时刻的值受到x-2, x-1, x, x+1, x+2共5个时刻的影响,其加权系数分别是0.01, 0.2, 1, 0.8, 0.05。也就是说(f*g)(x)=f(x-2)*0.01+f(x-1)*0.2+f(x)*1+f(x+1)*0.8+f(x+2)*0.05。其他x取值都是g(x)=0那么乘积项f(t)*g(x-t)也是0,因此在计算(f*g)(x)时可以不计。
从函数图像来看,比较函数f(x)的曲线和卷积后的函数(f*g)(x)的曲线,不难发现,卷积后的曲线比f(x)变得光滑一些。也就是说卷积运算能将f(x)函数的光滑度提高一阶。
Matlab程序代码
以下Matlab程序源代码实现了上例卷积运算,并且将f(x),g(x),(f*g)(x)的图像在同一坐标系中绘制出来。
clear; N=11;
x=[-5,-4,-3,-2,-1,0,1,2,3,4,5];
g=[0,0,0,0.05,0.8,1,0.2,0.01,0,0,0];
f=[1,4,3,6,2,3,1,4,5,3,4];
s=0;
f_g=zeros(1,N);
for xi=-5 : 5
index_xi=xi+6;
s=0;
for ti=-5:5
index_ti=ti+6;
if xi-ti<-5 || xi-ti>5
item=0;
else
index_xi_ti=xi-ti+6;
item=f(index_ti)*g(index_xi_ti);
end
s=s+item;
end
f_g(1,index_xi)=s;
end
hold on;
plot(x,f,'-o')
str=[ repmat(' ',N,1) num2str(f',2) ];
text(x,f,cellstr(str));
plot(x,g,'-o');
str=[ repmat(' ',N,1) num2str(g',2)];
text(x,g,cellstr(str));
plot(x,f_g,'-o');
str=[ repmat(' ',N,1) num2str(f_g',3) ];
text(x,f_g,cellstr(str));
hold off;