特征选择方法详解Part3-SelectFromModel-RFE、L1、Tree、Permutation importance

特征选择系列：

1. 特征选择方法详解Part1-方差分析、Pearson、Spearman

2. 特征选择方法详解Part2-卡方检验、互信息(Mutual Information)

3. 特征选择方法详解Part3-SelectFromModel-RFE、L1、Tree、Permutation importance

到目前为止，已经在《特征选择方法详解Part1-方差分析、Pearson、Spearman》和《特征选择方法详解Part2-卡方检验、互信息(Mutual Information)》2篇博文中，详细总结了特征选择的基本方法专家推荐、方差分析和单变量相关性分析方法Pearson、Spearman、卡方检验、互信息方法。本文将最后介绍一下基于模型的特征选择方法，主要包括sklearn中的RFE、基于L1正则化的方法、基于树模型的方法还有python库eli5提供的方法Permutation importance，本文偏向于应用，理论比较少。

文章同步发在我的个人博客，欢迎大佬们指教。特征选择方法详解Part3-SelectFromModel-RFE、L1、Tree、Permutation importance

1. 基于模型的特征选择方法

1.1 RFE(Recursive feature elimination)

1.1.1 原理

这个方法其实比较简单，就是使用机器学习模型不断的去训练模型，每训练一个模型，就去掉一个最不重要的特征，直到特征达到指定的数量。从上面的描述可知，所使用的模型能表示出特征重要性排序。在sklearn中，带有coef_ 和 ‌feature_importances_ 的模型都可以，这样的模型比较多，基于树的模型、线性的一系列模型大都满足要求，具体选择哪个，可以多尝试。

1.1.2 使用示例

sklearn.feature_selection.RFE方法和sklearn.feature_selection.RFECV方法实现了这种方法，两者的区别是，后者使用了交叉验证。这里直接给出sklearn文档中的例子：

>>> from sklearn.datasets import make_friedman1
>>> from sklearn.feature_selection import RFECV
>>> from sklearn.svm import SVR
>>> X, y = make_friedman1(n_samples=50, n_features=10, random_state=0)
>>> estimator = SVR(kernel="linear")
>>> selector = RFECV(estimator, step=1, cv=5)
>>> selector = selector.fit(X, y)
>>> selector.support_  # 值为True的列表示被选择的特征
array([ True,  True,  True,  True,  True, False, False, False, False, False])

1.2 基于L1正则化的方法

1.2.1 原理

要理解为什么L1范数能进行特征选择，那就要从正则化说起，正则化是一种防止机器学习模型过拟合的方法，它的具体实现是在机器学习模型的损失函数加上一个惩罚项，即正则化项，其一般形式如下：

$$Lossfunction=\sum _{i=1}^{N}L(f(x_i),y_i)+\lambda J(w_i)$$

上式中的 $J(w_i)$ 函数即是正则化项，上式中的第一项称为期望损失。为什么能正则化项能起到防止过拟合的作用呢？模型过拟合，表现在其在训练集上表现的比较好，但泛化能力差。如果每个样本都是一个点，那过拟合的模型会剧烈的上下抖动尽力穿过每一个点，这样模型参数 $w_i$ 绝对值就比较大。在训练模型时，实际上不断的迭代模型参数 $w_i$ 使损失函数最小，为了达到这个目的，损失函数就希望期望损失和正则化项都较小，而实际上期望损失变小则正则化项就变大，两者不断博弈，最后达到一个最优的状态。这时候实际上对于无用的特征，其 $w_i$ 就会变的很小，这也是上节中RFE方法的基础所在。

回到L1正则化，其公式如下：

$$J(w_i)=|W{|}_1=\sum _{i=1}^N|w_i|$$

L1正则化有一个不一样的特点，当使用带正则化项的损失函数，当模型达到最优，无用特征前面的系数 $w_i$ 就会变成0，也就是起到了特征选择的作用。注意到上面公式正则化项前都有一个参数 $\lambda$ ，其是控制惩罚程度的参数，其越大越不容易过拟合。在特征选择时，其越大，则系数为0的特征越多。

在sklearn文档中，官方建议：如果是回归任务， 使用linear_model.Lasso做特征选择，其实L1又叫Lasso，Lasso模型损失函数的公式如下：

$$\frac{1}{2n}\sum _{i=1}^N||y_i-f(x_i,w_i)|{|}^2+\lambda ||W|{|}_1$$

如果是分类任务，使用逻辑回归linear_model.LogisticRegression和核为线性核的SVMsvm.LinearSVC。

1.2.2 使用示例

>>> from sklearn.svm import LinearSVC
>>> from sklearn.datasets import load_iris
>>> from sklearn.feature_selection import SelectFromModel
>>> X, y = load_iris(return_X_y=True)
>>> X.shape
(150, 4)
>>> lsvc = LinearSVC(C=0.01, penalty="l1", dual=False).fit(X, y)
>>> model = SelectFromModel(lsvc, prefit=True)
>>> X_new = model.transform(X)
>>> X_new.shape
(150, 3)

1.3 基于树模型的方法

1.3.1 原理

在《特征选择方法详解Part2-卡方检验、互信息(Mutual Information)》一文中，详细介绍了互信息方法。实际上经典决策树模型ID3，就是通过互信息，即信息增益实现建模的。后来的决策树模型C4.5使用信息增益率进行建模，无论哪种方法，都是先从“对数据集纯度影响大的特征”开始分支的，实际上建树的过程，就是特征选择的过程，也是特征重要性排序的过程。

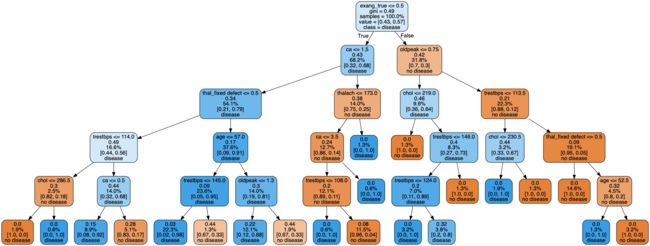
这里附上一张我原来输出过的决策树的图，感性的看一下决策树长什么样（可点击看高清图），越靠近根部的特征越重要：

1.3.2 使用示例

在sklearn中基于树的模型都可以做特征选择，主要包括树模型库sklearn.tree下面的树模型和集成学习方法库sklearn.ensemble下面的基于树的模型。同样，给一个官方文档中的例子。

>>> from sklearn.ensemble import ExtraTreesClassifier
>>> from sklearn.datasets import load_iris
>>> from sklearn.feature_selection import SelectFromModel
>>> X, y = load_iris(return_X_y=True)
>>> X.shape
(150, 4)
>>> clf = ExtraTreesClassifier(n_estimators=50)
>>> clf = clf.fit(X, y)
>>> clf.feature_importances_  
array([ 0.04...,  0.05...,  0.4...,  0.4...])
>>> model = SelectFromModel(clf, prefit=True)
>>> X_new = model.transform(X)
>>> X_new.shape               
(150, 2)

1.4 Permutation importance

1.4.1 原理

这个原理真的很简单：依次打乱数据集中每一个特征数值的顺序，其实就是做shuffle，然后观察模型的效果，下降的多的说明这个特征对模型比较重要。没了。

1.4.2 使用示例

下面示例中，参数model表示已经训练好的模型（支持sklearn中全部带有coef_ 和 ‌feature_importances_ 的模型，部分pytorch和keras训练的深度学习模型）

>>> import eli5
>>> from eli5.sklearn import PermutationImportance

>>> perm = PermutationImportance(model, random_state=20).fit(test_x, test_y)
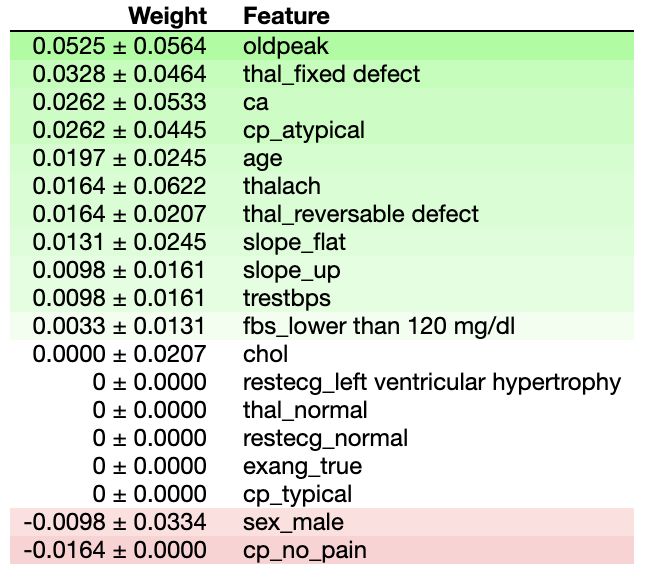
>>> eli5.show_weights(perm, feature_names=test_x.columns.tolist())

上面代码的输出见下图：

2. 结束

到这里，特征选择的所有方法就结束了。接下来一段时间可能专注于写深度学习领域的一些东西了。欢迎一起学习交流。