最小公倍数算法分析
一、实验内容
运行最大公约数的常用算法,并进行程序的调式与测试,要求程序设计风格良好,并添加异常处理模块(如输入非法等)。
二、算法
1.辗转相除法
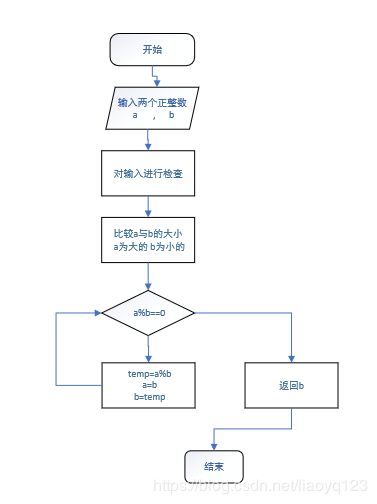
辗转相除法(又名欧几里德法)C语言中用于计算两个正整数a,b的最大公约数和最小公倍数,实质它依赖于下面的定理:

根据这一定理可以采用函数嵌套调用和递归调用形式进行求两个数的最大公约数和最小公倍数,现分别叙述如下
// 非递归实现:
public int divisor (int a,int b) /*自定义函数求两数的最大公约数*/
{
int temp; /*定义整型变量*/
if(a<b) /*通过比较求出两个数中的最大值和最小值*/
{ temp=a;a=b;b=temp;} /*设置中间变量进行两数交换*/
while(b!=0) /*通过循环求两数的余数,直到余数为0*/
{
temp=a%b;
a=b; /*变量数值交换*/
b=temp;
}return (a); /*返回最大公约数到调用函数处*/
}
// 递归实现:
public int gcd (int a,int b)
{
if(a%b==0)
return b;
else
return gcd(b,a%b);}
2.穷举法(利用数学定义)
穷举法(也叫枚举法)穷举法求两个正整数的最大公约数的解题步骤:从两个数中较小数开始由大到小列举,直到找到公约数立即中断列举,得到的公约数便是最大公约数 。
//非递归实现:
public int divisor (int a,int b) /*自定义函数求两数的最大公约数*/
{
int temp; /*定义义整型变量*/
temp=(a>b)?b:a; /*采种条件运算表达式求出两个数中的最小值*/
while(temp>0)
{
if (a%temp==0&&b%temp==0) /*只要找到一个数能同时被a,b所整除,则中止循环*/
break;
temp--; /*如不满足if条件则变量自减,直到能被a,b所整除*/
}
return (temp); /*返回满足条件的数到主调函数处*/
}
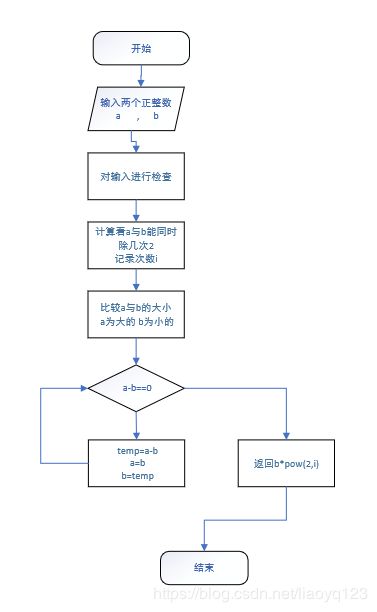
*3. 更相减损法
更相减损术,是出自《九章算术》的一种求最大公约数的算法,它原本是为约分而设计的,但它适用于任何需要求最大公约数的场合。《九章算术》是中国古代的数学专著,其中的“更相减损术”可以用来求两个数的最大公约数,即“可半者半之,不可半者,副置分母、子之数,以少减多,更相减损,求其等也。以等数约之。”
翻译成现代语言如下:
第一步:任意给定两个正整数;判断它们是否都是偶数。若是,则用2约简;若不是则执行第二步。
第二步:以较大的数减较小的数,接着把所得的差与较小的数比较,并以大数减小数。继续这个操作,直到所得的减数和差相等为止。
则第一步中约掉的若干个2与第二步中等数的乘积就是所求的最大公约数。
其中所说的“等数”,就是最大公约数。求“等数”的办法是“更相减损”法。所以更相减损法也叫等值算法。
// 非递归实现:
public int divisor(int m,int n)
{
int i=0,temp,x;
while(m%2==0 && n%2==0) //判断m和n能被多少个2整除
{
m/=2;
n/=2;
i+=1; //i保存能同时除掉的2的个数
}
if(m<n) //m保存大的值
{
temp=m;
m=n;
n=temp;
}
while(true)
{
x=m-n; // m与n相相减
m=(n>x)?n:x; //把相减后差与被减数中大的放入m
n=(n<x)?n:x; //把相减后差与被减数中小的的放入n
if(0==(m-n)) //直到被减数与差相等
break;
}
if(i==0)
return n;
else
return (int)Math.pow(2,i)*n;
}
4.Stein算法
Stein算法由J. Stein 1961年提出,这个方法也是计算两个数的最大公约数。
对两个正整数 x>y :
1.均为偶数 gcd( x,y ) =2gcd( x/2,y/2 );
2.均为奇数 gcd( x,y ) = gcd( (x+y)/2,(x-y)/2 );
2.x奇y偶 gcd( x,y ) = gcd( x,y/2 );
3.x偶y奇 gcd( x,y ) = gcd( x/2,y ) 或 gcd( x,y )=gcd( y,x/2 );
5.gcd( x,x ) = x ,退出条件。
//非递归实现:
public int divisor( int x, int y )
{
int factor = 0;
int temp;
if ( x < y ) //比较大小 x存储大的 y存储小的
{
temp = x;
x = y;
y = temp;
}
if ( 0 == y )
{
return 0;
}
while ( x != y )
{
if ( x%2!=0 )
{/*当x为奇数时 */
if ( y%2!=0 )
{/* 当x和y都是奇数时 */
y = ( x - y ) >> 1;
x -= y;
}
else
{/* 当x为奇数 y为偶数时 */
y >>= 1;
}
}
else
{/* 当x为偶数时 */
if ( y%2!=0 )
{/* 当x为偶数 y为奇数时 */
x >>= 1;
if ( x < y )
{
temp = x;
x = y;
y = temp;
}
}
else
{/* 当x和y都为偶数时 */
x >>= 1;
y >>= 1;
++factor;
}
}
}
return ( x << factor );
}
//递归实现:
public int gcd(int u,int v)
{
if (u == 0) return v;
if (v == 0) return u;
if (u%2==0) // u是偶数
{
if (v%2!=0) //u是偶数 v是奇数
return gcd(u >> 1, v);
else // u和v都是偶数
return gcd(u >> 1, v >> 1) << 1;
}
if (v%2==0) // u是奇数 v是偶数
return gcd(u, v >> 1);
// u和v都是奇数
if (u > v)
return gcd((u - v) >> 1, v);
return gcd((v - u) >> 1, u);
}
程序流程图:


四、总结
经过自己的动手实验,由最后的结果可知对于四种算法,枚举法的效率最低,其次是stein算法,再次是更相减损术;辗转相除法的效率最高。由于是随机产生的数字,这个结果只能代表一部分。下面我们来仔细分析一下各种算法:
对于辗转相除法相除数,在随机产生的整数中效率最高,其时间复杂度是对数量级O(log n)的,但对特别大的两个质数的效率就不太尽如人意。
对于更相减损术,其时间复杂度是O(n),特别是在两个数相差很时候,效率最差,比如999与1,要进行998减法运算。
对于枚举法,其时间复杂度也是O(n)数量级的,但他只对两个数相差很大的时候并且其中一个数较小时,才效率高。
对同一算法的非递归实现与递归实现,由于现在的计算机内存都特别大,在数据量小的时候,并看不出效率上的差异。
对于stein算法,是针对辗转相除法在对大整数进行运算时,需要试商导致增加运算时间的缺陷而提出的改进算法。其时间复杂度也是对数量级的,但由于stein算法是除法但嵌套导致其实际效率还不如更相减损术,只又在大质数的时候能由于辗转相除法。
在实验中遇到最多的bug,是对零的处理。零有没有约数?零与一个整数有没有公倍数?
由于我对数论了解甚少,网上有两种说法:
① 任意整数和0的公约数是该整数的所有约数
它们的最大公约数为该整数本身
因为0被所有非0整数整除,所以任意非零的整数都是0的约数
② 根据定义:如果一个整数能被另一个整数整除,那么第二个整数就是第一个整数的约数.约数是有限的,一般用最大公约数. 0既不是质数也不是合数 且他没有任何约数
为了方便处理,我采取了第二种说法,对输入进行判断,如果是输入零就直接返回零不做处理。在产生随机数的时候,也规避了产生零。
在stein算法中,用到了以为运算符>>来进行除二处理,我分别用/2与>>1进行了替换比较发现>>的效率比除法高了不少。