数据挖掘——谱聚类（spectral clustering）基本原理及python实现

一、前言

  谱聚类（spectral clustering）是广泛使用的聚类算法，比起传统的K-Means算法，谱聚类对数据分布的适应性更强，聚类效果也很优秀，同时聚类的计算量也小很多，更加难能可贵的是实现起来也不复杂。

  在处理实际的聚类问题时，个人认为谱聚类是应该首先考虑的几种算法之一。

二、基本原理

  谱聚类是从图论中演化出来的算法，后来在聚类中得到了广泛的应用。它的主要思想是把所有的数据看做空间中的点，这些点之间可以用边连接起来。距离较远的两个点之间的边权重值较低，而距离较近的两个点之间的边权重值较高，通过对所有数据点组成的图进行切图，让切图后不同的子图间边权重和尽可能的低，而子图内的边权重和尽可能的高，从而达到聚类的目的。

  这个算法原理的确简单，但是要完全理解这个算法的话，需要对图论中的无向图，线性代数和矩阵分析都有一定的了解。下面我们就从这些需要的基础知识开始，一步步学习谱聚类。

(一) 无向权重图

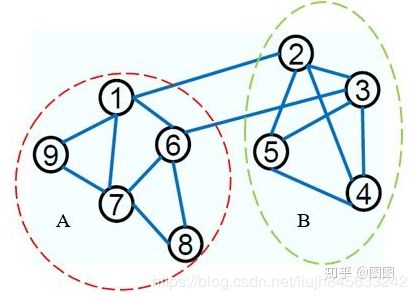
  由于谱聚类是基于图论的，因此我们学习一下图的概念。对于一个图 $G$，一般用点的集合 $V$和边的集合$E$ 来描述。即为 $G(V,E)$ 。其中$V$ 即为我们数据集里面所有的点$V=(v_1,v_2,...,v_n)$ 。对于 $V$ 中的任意两个点，可以有边连接，也可以没有边连接。我们定义权重$w_{ij}$为点$v_i$ 和点$v_j$之间的权重。由于我们是无向图，所以 $W_{ij}=W_{ji}$。如下图：

1、 邻接矩阵 W

  对于有边连接的两个点$v_i$和 $v_j$ ，$w_{ij}>0$，对于没有边连接的两个点 $v_i$和 $v_j$ ， $w_{ij}=0$ .

  对上面给定的图，如果我们认为连接的节点的权值是$1$，没有连接的节点的权值为$0$ ，则此时我们可以得到一个权值矩阵$W$：

  其中红色数字表示节点的标号，图中的每一行和每一列是对称的，他们都反映了该节点与其他节点的连接情况。

2、 度 D

  定义顶点的度为该顶点与其他顶点连接权值之和：
$$d_i=\sum _{j=1}^N{w}_{ij}$$
  利用每个点度的定义，我们可以得到一个nxn的度矩阵D,它是一个对角矩阵，只有主对角线有值，对应第$i$行的第$i$个点的度数，定义如下：
$$\mathbf{D}=\left(\begin{array}{ccc}{d}_1& .& .\\ .& d_2& .\\ ⋮& \cdots & ⋮\\ .& .& d_n\end{array}\right)$$
上面图对应的度矩阵为：

（二）相似矩阵/邻接矩阵 W

  上面我们讲到了邻接矩阵$W$，它是由任意两点之间的权重值$w_{ij}$组成的矩阵。通常我们可以自己输入权重，但是在谱聚类中，我们只有数据点的定义，并没有直接给出这个邻接矩阵，那么怎么得到这个邻接矩阵呢？

  基本思想是： 距离较远的两个点之间的边权重值较低，而距离较近的两个点之间的边权重值较高，不过这仅仅是定性，我们需要定量的权重值。一般来说，我们可以通过样本点距离度量的相似矩阵$S$来获得邻接矩阵$W$。

  构建邻接矩阵$W$的方法有三类。ϵ-邻近法，K邻近法和全连接法。

1、ϵ-邻近法

  它设置了一个距离阈值ϵ， 然后用欧氏距离 $s_{ij}$ 度量任意两点 $x_i$ 和 $x_j$ 的距离。即相似距离 $s_{ij}={\Vert x_i-x_j\Vert }_2^2$，然后根据$s_{ij}$ 和 ϵ 的大小关系，来定义邻接矩阵$W$ 如下：
$$W_{ij}=\{\begin{array}{cc}0& s_{ij}>ϵ\\ ϵ& s_{ij}>ϵ\end{array}$$
  从上式可见，两点的权重要不就是$ϵ$， 要不就是0， 没有其他信息了。距离远近度量很不精确，因此在实际应用中，我们很少使用$ϵ$-邻近法

2、K邻近法

  利用KNN算法遍历所有的样本点，取每个样本最近的$k$个点作为近邻，只有和样本距离最近的$k$个点之间的 $w_{ij}>0$。但是这种方法会造成重构之后的邻接矩阵$W$非对称，我们后面的算法需要对称邻接矩阵。为了解决这种问题，一般采取下面两种方法之一：

  第一种K 邻近法是只要一个点在另一个点的K 近邻中，则保留 $S_{ij}$
$$W_{ij}=W_{ji}=\{\begin{array}{cc}0& x_i\notin KNN(x_j)and{x}_j\notin KNN(x_i)\\ exp(-\frac{\Vert x_i-x_j\Vert }{2{\sigma }^2})& x_i\in KNN(x_j)or{x}_j\in KNN(x_i)\end{array}$$

  第二种K 邻近法是必须两个点互为K 近邻中，才能保留 $S_{ij}$
$$W_{ij}=W_{ji}=\{\begin{array}{cc}0& x_i\notin KNN(x_j)or{x}_j\notin KNN(x_i)\\ exp(-\frac{\Vert x_i-x_j\Vert }{2{\sigma }^2})& x_i\in KNN(x_j)and{x}_j\in KNN(x_i)\end{array}$$

3、全连接法

  相比前两种方法，第三种方法所有的点之间的权重值都大于0，因此称之为全连接法。

  可以选择不同的核函数来定义边权重，常用的有多项式核函数，高斯核函数和Sigmoid核函数。最常用的是高斯核函数RBF，此时相似矩阵和邻接矩阵相同：
$$W_{ij}=S_{ij}=exp(-\frac{{\Vert x_i-x_j\Vert }_2^2}{2{\sigma }^2})$$
  在实际的应用中，使用第三种全连接法来建立邻接矩阵是最普遍的，而在全连接法中使用高斯径向核RBF是最普遍的。

（三）拉普拉斯矩阵

  拉普拉斯矩阵（Laplacian matrix)），也称为基尔霍夫矩阵, 是表示图的一种矩阵。给定一个有n个顶点的图，其拉普拉斯矩阵被定义为:
$$L=D-W$$
  其中$D$为图的度矩阵，$W$为图的邻接矩阵。
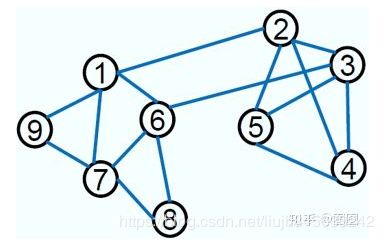
  举个例子。给定一个简单的图，如下：

把此“图”转换为邻接矩阵的形式，记为：$W$

  把的每一列元素加起来得到个数，然后把它们放在对角线上（其它地方都是零），组成一个$N\times N$对角矩阵，记为度矩阵$D$，如下图所示：

根据拉普拉斯矩阵的定义$L=D-W$，可得拉普拉斯矩阵 $L$为：

(2) 拉普拉斯矩阵的性质

拉普拉斯矩阵 具有如下性质：

• 拉普拉斯矩阵是对称半正定矩阵，这可以由 $D$和$W$都是对称矩阵而得；
• $L1=01$，即 $L$ 的最小特征值是 0，相应的特征向量是 $1$。证明：$L\ast 1=(D-W)\ast 1=0=0\ast 1$。（此外，别忘了，之前特征值和特征向量的定义：若数字 $\lambda$ 和非零向量 $v$ 满足$Av=\lambda v$，则$\lambda$ 为的$A$一个特征向量，$v$ 是其对应的特征值）。
• $L$ 有n个非负实特征值 $0={\lambda }_1⩽{\lambda }_2⩽...⩽{\lambda }_n$
• 且对于任何一个属于实向量 $f\in {\mathbb{R}}^n$，有以下式子成立:
  $$f^{T}Lf=\frac{1}{2}\sum _{i,j=1}n{w}_{ij}(f_i-f_j{)}^2$$

  这个利用拉普拉斯矩阵的定义很容易得到如下：
$$\begin{array}{rl}{f}^{T}Lf& =f^{T}Df-f^{T}Wf\\ & =\sum _{i=1}^n{d}_i{f}_i^2-\sum _{i,j=1}^n{w}_{ij}{f}_i{f}_j\\ & =\frac{1}{2}(\sum _{i=1}^n{d}_i{f}_i^2-2\sum _{i,j=1}^n{w}_{ij}{f}_i{f}_j+\sum _{j=1}^n{d}_j{f}_j^2)\\ & =\frac{1}{2}\sum _{i,j=1}^n{w}_{ij}(f_i-f_j{)}^2\end{array}$$

(四) 无向图切图

1、 子图与子图的连接权重

  对于无向图$G$的切图，我们的目标是将图$G(V,E)$切成相互没有连接的$k$个子图，每个子图点的集合为：
$${\mathbf{A}}_1,{\mathbf{A}}_2,...,{\mathbf{A}}_{\mathbf{k}}，它们满足{\mathbf{A}}_{\mathbf{i}}\cap {\mathbf{A}}_{\mathbf{j}}=\varnothing ，且{\mathbf{A}}_1\cup {\mathbf{A}}_2\cup ...\cup {\mathbf{A}}_{\mathbf{k}}=\mathbf{V}$$

  我们可以将下面的图划分成两个子图，如下图所示：

  定义 $A$和 $B$ 是图 $G$ 中两个子图，则定义子图$A$和 $B$的切图权重为：
$$\mathbf{W}(\mathbf{A},\mathbf{B}):=\sum _{\mathbf{i}\in \mathbf{A},\mathbf{j}\in \mathbf{B}}{\mathbf{w}}_{\mathbf{i}\mathbf{j}}$$

  那么对于我们$k$个子图的集合：${\mathbf{A}}_1,{\mathbf{A}}_2,...,{\mathbf{A}}_{\mathbf{k}}$ ， 我们定义切图 cut 为：
$$\mathbf{c}\mathbf{u}\mathbf{t}({\mathbf{A}}_1,{\mathbf{A}}_2,...,{\mathbf{A}}_{\mathbf{k}})=\frac{1}{2}\sum _{\mathbf{i}=1}^{\mathbf{k}}\mathbf{W}({\mathbf{A}}_{\mathbf{i}},{\bar{\mathbf{A}}}_{\mathbf{i}})$$
其中 ${\bar{A}}_i$ 为 $A_i$ 的补集。

2、 切图的目标函数

  那么如何切图可以让子图内的点权重和高，子图间的点权重和低呢？一个自然的想法就是最小化$\mathbf{c}\mathbf{u}\mathbf{t}({\mathbf{A}}_1,{\mathbf{A}}_2,...,{\mathbf{A}}_{\mathbf{k}})$，但是可以发现，这种极小化的切图存在问题，如下图：

  我们选择一个权重最小的边缘的点，比如$C$和$H$之间进行cut，这样可以最小化 $\mathbf{c}\mathbf{u}\mathbf{t}({\mathbf{A}}_1,{\mathbf{A}}_2,...,{\mathbf{A}}_{\mathbf{k}})$，但是却不是最优的切图，如何避免这种切图，并且找到类似图中"Best Cut"这样的最优切图呢？接下来就来看看谱聚类使用的切图方法。

(五) 谱聚类切图

  为了避免最小切图导致的切图效果不佳，我们需要对每个子图的规模做出限定，一般来说，有两种切图方式，第一种是RatioCut，第二种是Ncut。下面我们分别加以介绍。

1、 RatioCut切图

  RatioCut切图为了避免上面出现的最小切图，对每个切图，不光考虑最小化$\mathbf{c}\mathbf{u}\mathbf{t}({\mathbf{A}}_1,{\mathbf{A}}_2,...,{\mathbf{A}}_{\mathbf{k}})$ ，它还同时考虑最大化每个子图点的个数，即：
$$RatiocCut(A_1,A_2,...,A_k)=\frac{1}{2}\sum _{i=1}^k\frac{W(A_i,{\bar{A}}_i)}{\left|A_i\right|}$$
  那么怎么最小化这个RatioCut函数呢？牛人们发现，RatioCut函数可以通过如下方式表示:

  我们引入指示向量 $h_j=h_1,h_2,....,h_{k}j=1,2,...,k$，对于任意一个向量 $h_j$，它是一个n维向量，我们定义$h_{ij}$为：
$${\mathbf{h}}_{\mathbf{j}\mathbf{i}}=\{\begin{array}{cc}0& v_i\notin A_j\\ \frac{1}{\sqrt{|A_j|}}& v_i\in A_j\end{array}$$
  那么我们对于$h_i^{T}L{h}_i$有：
$$\begin{array}{rl}{h}_i^{T}L{h}_i& =\frac{1}{2}\sum _{m=1}\sum _{n=1}{w}_{mn}(h_{im}-h_{in}{)}^2\\ & =\frac{1}{2}(\sum _{m\in A_i,n\notin A_i}{w}_{mn}(\frac{1}{\sqrt{|A_i|}}-0{)}^2+\sum _{m\notin A_i,n\in A_i}{w}_{mn}(0-\frac{1}{\sqrt{\left|A_i\right|}}{)}^2)\\ & =\frac{1}{2}(\sum _{m\in A_i,n\notin A_i}{w}_{mn}\frac{1}{\left|A_i\right|}+\sum _{m\in A_i,n\notin A_i}{w}_{mn}\frac{1}{\left|A_i\right|})\\ & =\frac{1}{2}(cut(A_i,{\bar{A}}_i)\frac{1}{|A_i|}+cut(A_i,{\bar{A}}_i)\frac{1}{|A_i|})\\ & =\frac{cut(A_i,{\bar{A}}_i)}{|A_i|}\\ & =RatioCut(A_i,{\bar{A}}_i)\end{array}$$

  上述式子列出来的是对于某一个子图$i$，它的RatioCut对应于$h_i^{T}L{h}_i$, 那么对于k个子图，对应的RatioCut函数表达式为：
$$RatioCut(A_1,A_2,...,A_k)=\sum _{i=1}^k{h}_i^{T}L{h}_i=\sum _{i=1}^k(H^{T}LH{)}_{ii}=tr(H^{T}LH)$$
  其中 $tr(H^{T}LH)$ 为矩阵的迹。也就是说，我们的RatioCut切图，实际上就是最小化我们的$tr(H^{T}LH)$， 其中 $H^{T}H=I$,，则我们的切图优化目标为;
$$\mathbf{a}\mathbf{r}\mathbf{g}\mathbf{m}\mathbf{i}\mathbf{n}\mathbf{t}\mathbf{r}({\mathbf{H}}^{\mathbf{T}}\mathbf{L}\mathbf{H})\mathbf{s}.\mathbf{t}.{\mathbf{H}}^{\mathbf{T}}\mathbf{H}=\mathbf{I}$$

  注意到 $H$矩阵里面的每一个指示向量都是n维的，向量中每个变量的取值为0或者$\frac{1}{\sqrt{|A_i|}}$，就有$2^n$种取值，有k个子图的话就有k个指示向量，共有$k{2}^n$ 种 $H$，因此找到满足上面优化目标的$H$是一个NP难的问题。那么是不是就没有办法了呢？

  注意观察$tr(H^{T}LH)$ 中每一个优化子目标 $h_i^{T}L{h}_i$，其中$h$是单位正交基，$L$是对称矩阵，此时 $h_i^{T}L{h}_i$的最大值为$L$ 的最大特征值，最小值是$L$ 的最小特征值。如果你对主成分分析PCA很熟悉的话，这里很好理解。在PCA中，我们的目标是找到协方差矩阵（对应此处的拉普拉斯矩阵L）的最大的特征值，而在我们的谱聚类中，我们的目标是找到目标的最小的特征值，得到对应的特征向量，此时对应二分切图效果最佳。也就是说，我们这里要用到维度规约的思想来近似去解决这个NP难的问题。

  对于 $h_i^{T}L{h}_i$，目标是找到最小的 $L$的特征值，而对于 $tr(H^{T}LH)={\sum }_{i=1}^k{h}_i^{T}L{h}_i$ ，则我们的目标就是找到k个最小的特征值，一般来说，k远远小于n，也就是说，此时我们进行了维度规约，将维度从n降到了k，从而近似可以解决这个NP难的问题。

  通过找到L的最小的k个特征值，可以得到对应的k个特征向量，这k个特征向量组成一个nxk维度的矩阵，即为我们的H。一般需要对H里的每一个特征向量做标准化，即

$$h_i=\frac{h_i}{|h_i|}$$

  由于我们在使用维度规约的时候损失了少量信息，导致得到的优化后的指示向量h对应的H现在不能完全指示各样本的归属，因此一般在得到 $n\times k$ 维度的矩阵H后还需要对每一行进行一次传统的聚类，比如使用K-Means聚类.

2、 Ncut切图

  Ncut切图和RatioCut切图很类似，但是把Ratiocut的分母 $|A_i|$ 换成$vol(A_i)$ 。由于子图样本的个数多并不一定权重就大，我们切图时基于权重也更合我们的目标，因此一般来说Ncut切图优于RatioCut切图。

$$NCut(A_1,A_2,...,A_k)=\frac{1}{2}\sum _{i=1}^k\frac{W(A_i,{\bar{A}}_i)}{vol(A_i)}$$
  对应的NCut切图对指示向量$h_{ij}$做了改进，注意到RatioCut切图的指示向量使用的是$\frac{1}{\sqrt{|A_j|}}$标示样本归属，而Ncut切图使用了子图权重$\frac{1}{\sqrt{vol(A_j|)}}$来标示指示向量h，定义如下：

$${\mathbf{h}}_{\mathbf{j}\mathbf{i}}=\{\begin{array}{cc}0& v_i\notin A_j\\ \frac{1}{\sqrt{vol\left(A_j\right)}}& v_i\in A_j\end{array}$$
  那么我们对于$h_i^{T}L{h}_i$有：
$$\begin{array}{rl}{h}_i^{T}L{h}_i& =\frac{1}{2}\sum _{m=1}\sum _{n=1}{w}_{mn}(h_{im}-h_{in}{)}^2\\ & =\frac{1}{2}(\sum _{m\in A_i,n\notin A_i}{w}_{mn}(\frac{1}{\sqrt{vol(A_i)}}-0{)}^2+\sum _{m\notin A_i,n\in A_i}{w}_{mn}(0-\frac{1}{\sqrt{vol\left(A_i\right)}}{)}^2)\\ & =\frac{1}{2}(\sum _{m\in A_i,n\notin A_i}{w}_{mn}\frac{1}{vol\left(A_i\right)}+\sum _{m\in A_i,n\notin A_i}{w}_{mn}\frac{1}{vol\left(A_i\right)})\\ & =\frac{1}{2}(cut(A_i,{\bar{A}}_i)\frac{1}{vol(A_i)}+cut(A_i,{\bar{A}}_i)\frac{1}{vol(A_i)})\\ & =\frac{cut(A_i,{\bar{A}}_i)}{vol(A_i)}\\ & =NCut(A_i,{\bar{A}}_i)\end{array}$$

  推导方式和RatioCut完全一致。也就是说，我们的优化目标仍然是

$$NCut(A_1,A_2,...,A_k)=\sum _{i=1}^k{h}_i^{T}L{h}_i=\sum _{i=1}^k(H^{T}LH{)}_{ii}=tr(H^{T}LH)$$
  但是，此时的 $H^{T}H=I$,，而是$H^{T}DH=I$, 推导如下：

$$h_i^{T}D{h}_i=\sum _{j=1}^n{h}_{ij}^2{d}_j=\frac{1}{vol(A_i)}\sum _{v_j\in A_i}{w}_{v_j}=\frac{1}{vol(A_i)}vol(A_i)=I$$
$$\mathbf{a}\mathbf{r}\mathbf{g}\mathbf{m}\mathbf{i}\mathbf{n}\mathbf{t}\mathbf{r}({\mathbf{H}}^{\mathbf{T}}\mathbf{L}\mathbf{H})\mathbf{s}.\mathbf{t}.{\mathbf{H}}^{\mathbf{T}}\mathbf{D}\mathbf{H}=\mathbf{I}$$

  此时我们的H中的指示向量h并不是标准正交基，所以在RatioCut里面的降维思想不能直接用。怎么办呢？其实只需要将指示向量矩阵H做一个小小的转化即可。

  我们令$H=D^{-1/2}F$, 则：$H^{T}LH=F^T{D}^{-1/2}L{D}^{-1/2}F$，$H^{T}DH=F^{T}F=I$,也就是说优化目标变成了:
$$argmintr(F^T{D}^{-1/2}L{D}^{-1/2}F)s.t.F^{T}F=I$$

  可以发现这个式子和RatioCut基本一致，只是中间的L变成了$D^{-1/2}L{D}^{-1/2}$ 。这样我们就可以继续按照RatioCut的思想，求出$D^{-1/2}L{D}^{-1/2}$ 的最小的前k个特征值，然后求出对应的特征向量，并标准化，得到最后的特征矩阵F,最后对F进行一次传统的聚类（比如K-Means）即可。

  一般来说，$D^{-1/2}L{D}^{-1/2}$相当于对拉普拉斯矩阵L做了一次标准化，即 $\frac{L_{ij}}{\sqrt{d_i\ast d_j}}$

三、谱聚类算法流程

  铺垫了这么久，终于可以总结下谱聚类的基本流程了。一般来说，谱聚类主要的注意点为相似矩阵的生成方式，切图的方式以及最后的聚类方法.

  最常用的相似矩阵的生成方式是基于高斯核距离的全连接方式，最常用的切图方式是Ncut。而到最后常用的聚类方法为K-Means。下面以Ncut总结谱聚类算法流程。

输入： 样本集$D=(x_1,x_2,...,x_n)$，相似矩阵的生成方式, 降维后的维度$k_1$, 聚类方法，聚类后的维度 $k_2$
　　　　
输出： 簇划分$C(c_1,c_2,...c_{k_2})$

1）根据输入的相似矩阵的生成方式构建样本的相似矩阵$S$
2）根据相似矩阵$S$构建邻接矩阵$W$，构建度矩阵$D$
3）计算出拉普拉斯矩阵$L$
4）构建标准化后的拉普拉斯矩阵$D^{-1/2}L{D}^{-1/2}$
5）计算$D^{-1/2}L{D}^{-1/2}$最小的$k_1$个特征值所各自对应的特征向量$f$
6) 将各自对应的特征向量$f$组成的矩阵按行标准化，最终组成$n\times k_1$维的特征矩阵$F$
7）对$F$中的每一行作为一个$k_1$维的样本，共n个样本，用输入的聚类方法进行聚类，聚类维数为$k_2$。
8）得到簇划分$C(c_1,c_2,...c_{k_2})$

四、python实现

import numpy as np
from sklearn.cluster import KMeans
import math
import matplotlib.pyplot as plt

def load_data(filename):
    """
    载入数据
    :param filename: 文件名
    :return:
    """
    data = np.loadtxt(filename, delimiter='\t')
    return data

def distance(x1, x2):
    """
    获得两个样本点之间的距离
    :param x1: 样本点1
    :param x2: 样本点2
    :return:
    """
    dist = np.sqrt(np.power(x1-x2,2).sum())
    return dist

def get_dist_matrix(data):
    """
    获取距离矩阵
    :param data: 样本集合
    :return: 距离矩阵
    """
    n = len(data)  #样本总数
    dist_matrix = np.zeros((n, n)) # 初始化邻接矩阵为n×n的全0矩阵
    for i in range(n):
        for j in range(i+1, n):
            dist_matrix[i][j] = dist_matrix[j][i] = distance(data[i], data[j])
    return dist_matrix

def getW(data, k):
    """
    获的邻接矩阵 W
    :param data: 样本集合
    :param k : KNN参数
    :return: W
    """
    n = len(data)
    dist_matrix = get_dist_matrix(data)
    W = np.zeros((n, n))
    for idx, item in enumerate(dist_matrix):
        idx_array = np.argsort(item)  # 每一行距离列表进行排序,得到对应的索引列表
        W[idx][idx_array[1:k+1]] = 1
    transpW =np.transpose(W)
    return (W+transpW)/2

def getD(W):
    """
    获得度矩阵
    :param W: 邻接矩阵
    :return: D
    """
    D = np.diag(sum(W))
    return D


def getL(D,W):
    """
    获得拉普拉斯矩阵
    :param W: 邻接矩阵
    :param D: 度矩阵
    :return: L
    """
    return D-W

def getEigen(L, cluster_num):
    """
    获得拉普拉斯矩阵的特征矩阵
    :param L:
    :param cluter_num: 聚类数目
    :return:
    """
    eigval, eigvec = np.linalg.eig(L)
    ix = np.argsort(eigval)[0:cluster_num]
    return eigvec[:, ix]

def plotRes(data, clusterResult, clusterNum):
    """
    结果可似化
    :param data:  样本集
    :param clusterResult: 聚类结果
    :param clusterNum: 聚类个数
    :return:
    """
    n = len(data)
    scatterColors = ['black', 'blue', 'green', 'yellow', 'red', 'purple', 'orange']
    for i in range(clusterNum):
        color = scatterColors[i % len(scatterColors)]
        x1= []; y1=[]
        for j in range(n):
            if clusterResult[j] == i:
                x1.append(data[j,0])
                y1.append(data[j, 1])
        plt.scatter(x1, y1, c=color, marker='+')
    plt.show()


def cluster(data, cluster_num, k):
    data = np.array(data)
    W = getW(data, k)
    D = getD(W)
    L = getL(D,W)
    eigvec = getEigen(L, cluster_num)
    clf = KMeans(n_clusters=cluster_num)
    s = clf.fit(eigvec)  # 聚类
    label = s.labels_
    return  label


if __name__ == '__main__':
    cluster_num = 7
    knn_k = 5
    filename = '../data/Aggregation_cluster=7.txt'
    data = load_data(filename=filename)
    data = data[0:-1]  # 最后一列为标签列
    label = cluster(data, cluster_num, knn_k)
    plotRes(data, label, cluster_num)

运行结果如下：

五、sklearn库中的谱聚类使用

  在scikit-learn的类库中，sklearn.cluster.SpectralClustering实现了基于Ncut的谱聚类，没有实现基于RatioCut的切图聚类。同时，对于相似矩阵的建立，也只是实现了基于K邻近法和全连接法的方式，没有基于ϵϵ-邻近法的相似矩阵。最后一步的聚类方法则提供了两种，K-Means算法和 discretize算法。

  对于SpectralClustering的参数，我们主要需要调参的是相似矩阵建立相关的参数和聚类类别数目，它对聚类的结果有很大的影响。当然其他的一些参数也需要理解，在必要时需要修改默认参数。

• 1）n_clusters：代表我们在对谱聚类切图时降维到的维数，同时也是最后一步聚类算法聚类到的维数。也就是说scikit-learn中的谱聚类对这两个参数统一到了一起。简化了调参的参数个数。虽然这个值是可选的，但是一般还是推荐调参选择最优参数。

• 2) affinity: 也就是我们的相似矩阵的建立方式。可以选择的方式有三类，

  • 第一类是 **‘nearest_neighbors’**即K邻近法。
  • 第二类是**‘precomputed’**即自定义相似矩阵。选择自定义相似矩阵时，需要自己调用set_params来自己设置相似矩阵。
  • 第三类是全连接法，可以使用各种核函数来定义相似矩阵，还可以自定义核函数。最常用的是内置高斯核函数’rbf’。其他比较流行的核函数有‘linear’即线性核函数, ‘poly’即多项式核函数, ‘sigmoid’即sigmoid核函数。如果选择了这些核函数， 对应的核函数参数在后面有单独的参数需要调。自定义核函数我没有使用过，这里就不多讲了。affinity默认是高斯核’rbf’。一般来说，相似矩阵推荐使用默认的高斯核函数。

• 3) 核函数参数gamma: 如果我们在affinity参数使用了多项式核函数 ‘poly’，高斯核函数‘rbf’, 或者’sigmoid’核函数，那么我们就需要对这个参数进行调参。

  • 多项式核函数中这个参数对应$K(x,z)=（\gamma x\cdot z+r)d$中的$\gamma$。一般需要通过交叉验证选择一组合适的$\gamma ,r,d$
  • 高斯核函数中这个参数对应$K(x,z)=exp(-\gamma ||x-z|{|}^2)$中的$\gamma$。一般需要通过交叉验证选择合适的$\gamma$
  • sigmoid核函数中这个参数对应$K(x,z)=tanh（\gamma x\cdot z+r)$中的$\gamma$。一般需要通过交叉验证选择一组合适的$\gamma ,r$
  • $\gamma$默认值为1.0，如果我们affinity使用’nearest_neighbors’或者是’precomputed’，则这么参数无意义。

• 4）核函数参数degree：如果我们在affinity参数使用了多项式核函数 ‘poly’，那么我们就需要对这个参数进行调参。这个参数对应$K(x,z)=（\gamma x\cdot z+r)d$中的$d$。默认是3。一般需要通过交叉验证选择一组合适的$\gamma ,r,d$

• 5）核函数参数coef0: 如果我们在affinity参数使用了多项式核函数 ‘poly’，或者sigmoid核函数，那么我们就需要对这个参数进行调参。

  • 多项式核函数中这个参数对应$K(x,z)=（\gamma x\cdot z+r)d$中的$r$。一般需要通过交叉验证选择一组合适的$\gamma ,r,d$
  • sigmoid核函数中这个参数对应$K(x,z)=tanh（\gamma x\cdot z+r)$中的r。一般需要通过交叉验证选择一组合适的$\gamma ,r$
  • coef0默认为1.

• 6）kernel_params：如果affinity参数使用了自定义的核函数，则需要通过这个参数传入核函数的参数。

• 7 )n_neighbors: 如果我们affinity参数指定为’nearest_neighbors’即K邻近法，则我们可以通过这个参数指定KNN算法的K的个数。默认是10.我们需要根据样本的分布对这个参数进行调参。如果我们affinity不使用’nearest_neighbors’，则无需理会这个参数。

• 8）eigen_solver:1在降维计算特征值特征向量的时候，使用的工具。有 None, ‘arpack’, ‘lobpcg’, 和‘amg’4种选择。如果我们的样本数不是特别大，无需理会这个参数，使用’'None暴力矩阵特征分解即可,如果样本量太大，则需要使用后面的一些矩阵工具来加速矩阵特征分解。它对算法的聚类效果无影响。

• 9）eigen_tol：如果eigen_solver使用了arpack’，则需要通过eigen_tol指定矩阵分解停止条件。

• 10）assign_labels：即最后的聚类方法的选择，有K-Means算法和 discretize算法两种算法可以选择。一般来说，默认的K-Means算法聚类效果更好。但是由于K-Means算法结果受初始值选择的影响，可能每次都不同，如果我们需要算法结果可以重现，则可以使用discretize。

• 11）n_init：即使用K-Means时用不同的初始值组合跑K-Means聚类的次数，这个和K-Means类里面n_init的意义完全相同，默认是10，一般使用默认值就可以。如果你的n_clusters值较大，则可以适当增大这个值。

  从上面的介绍可以看出，需要调参的部分除了最后的类别数n_clusters，主要是相似矩阵affinity的选择，以及对应的相似矩阵参数。当我选定一个相似矩阵构建方法后，调参的过程就是对应的参数交叉选择的过程。对于K邻近法，需要对n_neighbors进行调参，对于全连接法里面最常用的高斯核函数rbf，则需要对gamma进行调参。

import numpy as np
from sklearn.cluster import SpectralClustering
from sklearn import metrics
import matplotlib.pyplot as plt

def load_data(filename):
    """
    载入数据
    :param filename: 文件名
    :return:
    """
    data = np.loadtxt(filename, delimiter='\t')
    return data


def plotRes(data, clusterResult, clusterNum):
    """
    结果可似化
    :param data:  样本集
    :param clusterResult: 聚类结果
    :param clusterNum: 聚类个数
    :return:
    """
    n = len(data)
    scatterColors = ['black', 'blue', 'green', 'yellow', 'red', 'purple', 'orange']
    for i in range(clusterNum):
        color = scatterColors[i % len(scatterColors)]
        x1= []; y1=[]
        for j in range(n):
            if clusterResult[j] == i:
                x1.append(data[j,0])
                y1.append(data[j, 1])
        plt.scatter(x1, y1, c=color, marker='+')
    plt.show()

if __name__ == '__main__':
    cluster_num = 7
    knn_k = 5
    filename = '../data/Aggregation_cluster=7.txt'
    datas = load_data(filename=filename)
    dataMat = np.mat(datas)  #转换为矩阵
    data = np.array(dataMat[:,0:-1])
    label = np.array(dataMat[:,-1])  # 最后一列为标签列
    ## 调参数============
    # for i, gamma in enumerate((0.01, 0.1)):
    #     for j, k in enumerate((3,4,5,6,7,8)):
    #         y_pred = SpectralClustering(n_clusters=k, gamma=gamma).fit_predict(data)
    #         print("Calinski-Harabasz Score with gamma=", gamma, "n_clusters=", k, "score:",
    #               metrics.calinski_harabaz_score(data, y_pred))
    ##########

    y_pred = SpectralClustering(gamma=0.1,n_clusters=7).fit_predict(data)
    print("Calinski-Harabasz Score", metrics.calinski_harabaz_score(data, y_pred))
    plotRes(data, y_pred, cluster_num)

六、谱聚类算法总结

谱聚类是一种基于数据相似度矩阵的聚类方法，它定义了子图划分的优化目标函数，并作出改进（RatioCut和NCut），引入指示变量，将划分问题转化为求解最优的指示变量矩阵HH。然后利用瑞利熵的性质，将该问题进一步转化为求解拉普拉斯矩阵的kk个最小特征值，最后将 HH 作为样本的某种表达，使用传统的聚类方法进行聚类。
  我对于谱聚类的理解是，原本相似度矩阵就是对样本点的一种特征表达（特征维数等于样本数），现在进行了谱聚类求得的特征值矩阵，实际上是对原始特征矩阵的一种降维（也可能是升维），总之就是将样本从原始空间变换（可能是线性的也可能是非线性的）到另一个空间，在这个空间中具有良好的全局欧式性。

参考资料：

• 论文：Shi, J., and J. Malik (1997) “Normalized Cuts and Image Segmentation”
• 论文：A Tutorial on Spectral Clustering
• 谱聚类（Spectral Clustering）原理及Python实现：https://blog.csdn.net/songbinxu/article/details/80838865
• 理解谱聚类 https://zhuanlan.zhihu.com/p/57369475
• 从拉普拉斯矩阵说到谱聚类：https://blog.csdn.net/guoxinian/article/details/79532893
• 谱聚类（spectral clustering）原理总结：https://www.cnblogs.com/pinard/p/6221564.html