115.不同的子序列
难度:困难
题目描述:
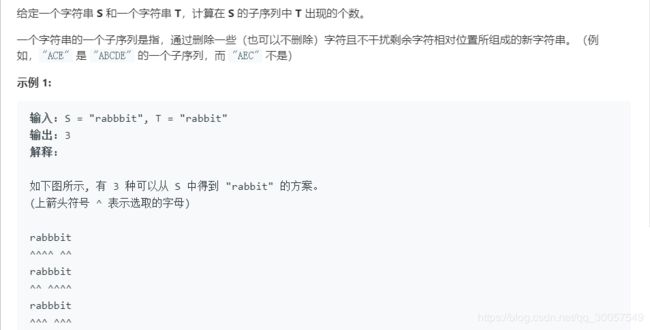
思路总结:动态规划,结合手写例子来理解更为清晰。题解一中算法解释来自这。
题解一:(动态规划)
- 状态
dp[i][j]为s1串中前i个字符中可以组成s2串前j个字符子序列的个数。 - 状态转移方程
- 如果s1[i]==s2[j],dp[i][j]=dp[i-1][j-1]+dp[i-1][j]
- 否则,dp[i][j]=dp[i-1][j]
note:具体解释见图片举得两个例子。
class Solution:
def numDistinct(self, s: str, t: str) -> int:
ns, nt = len(s), len(t)
#dp初始化
dp = [[1 if j==0 else 0 for j in range(nt+1)] for i in range(ns+1)]
#状态转移
for i in range(1, ns+1):
for j in range(1, nt+1):
dp[i][j] = dp[i-1][j]
if s[i-1] ==t[j-1]: #此处是因为行和列都增加了空串""
dp[i][j] += dp[i-1][j-1]
return dp[-1][-1]

