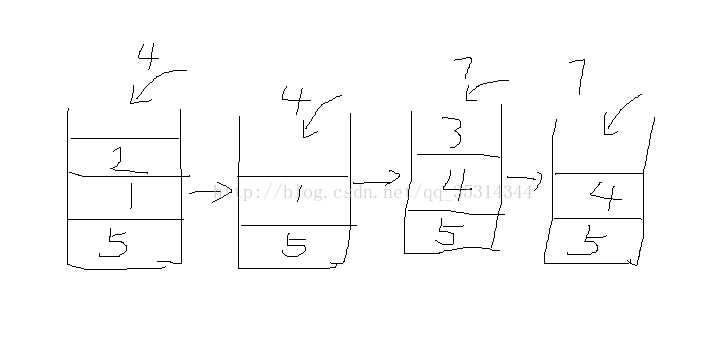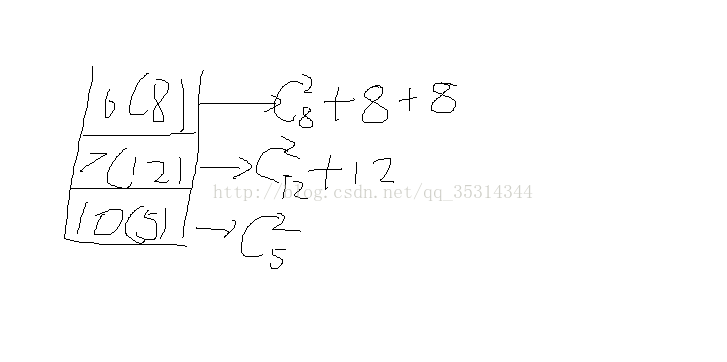左神面试算法整理---单调栈
小B负责首都的防卫工作。
首都处于一个四面环山的盆地中,周围的n个小山构成一个环,作为预警措施,小B计划在每个小山上设置一个观察哨,日夜不停的瞭望周围发生的情况。
一旦发生外敌入侵事件,山顶上的岗哨将点燃烽烟。
若两个岗哨所在的山峰之间的那些山峰,高度都不大于这两座山峰,且这两个山峰之间有相连通路,则岗哨可以观察到另一个山峰上的烽烟是否点燃。
由于小山处于环上,任意两个小山之间存在两个不同的连接通路。满足上述不遮挡的条件下,一座山峰上岗哨点燃的烽烟至少可以通过一条通路被另一端观察到。
对于任意相邻的岗哨,一端的岗哨一定可以发现一端点燃的烽烟。
小B设计的这种保卫方案的一个重要特性是能够观测到对方烽烟的岗哨对的数量,她希望你能够帮她解决这个问题。
输入
输入中有多组测试数据。每组测试数据的第一行为一个整数n(3<=n<=10^6),为首都周围的小山数量,第二行为n个整数,依次表示小山的高度h,(1<=h<=10^9)。
输出
对每组测试数据,在单独的一行中输出能相互观察到的岗哨的对数。
样例输入
5
1 2 4 5 3
样例输出
7
算法思想:
此题可以理解为在两个山峰之间的山峰都比两端低时,两端山峰就是一对,现在就是求有多少对?此题可以转为环形链表中,一个数求他左右两边离他最近且大于他的数。
(1,2)(1,3)(2,3)(2,4)(4,5)(3,4)(3,5)
可以看出最高和次高可以组成一对,其他数据都能有两个相邻最大值,所以此问题通解(n-2)*2+1。
找出一个数左右最近的大于他的数,可以用单调栈实现。我们设定单调栈中,从栈顶到栈底依次变大。
假设有数 5 2 1 4 3 7
先放5,2小于5,放2,1小于2,放1,4大于1,则1弹出,1的弹出是由于4,所以4是1右边临近的大于他的数,2在1下面,所以2是1左面临近大于他的数。相同原理2弹出,4进,3进,7进时同理弹出3,4,5
左 右
1 2 4
2 5 4
3 4 7
4 5 7
5 null 7
7 null null
总对数=4*2+1。此算法复杂度可以达到O(n),遍历算法O(n^2)
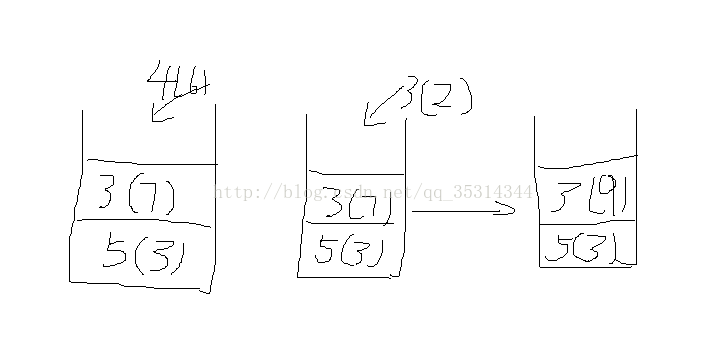
以上算法只适用于,山峰高度都各不相等的情况下,若有相等则:一次遍历将相邻相等山峰合并,二次遍历找最大值开始压栈
将3个5压入,7个3压入,当6个4压入时,7个3要出栈。7个3中,自己有对,与3相邻的4,可以看到每个3,所以有7对,5与4同理有7对,
共7*6/2+7+7。
当压入数据与栈顶数据相同,则只需合并个数即可。
没有数据入栈时,只需依次出栈,
纠正上图一个错误,对于7产生的个数,少加了一个12.因为只剩下7和10的时候,从10看向7和从7看向10是不一样的所以要加两次12
6是最后一个进栈的数,他要和栈底的数产生对数。
JAVA版
package problems_2017_07_26;
import java.util.Scanner;
import java.util.Stack;
public class Problem_04_MountainsAndFlames {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
while (in.hasNextInt()) {
int size = in.nextInt();
int[] arr = new int[size];
for (int i = 0; i < size; i++) {
arr[i] = in.nextInt();
}
System.out.println(communications(arr));
}
}
public static int nextIndex(int size, int i) {
return i < (size - 1) ? (i + 1) : 0;
//相邻相同山峰之间的对数,若只有一个,则没有成对,若有两个以上计算内部成对数
public static long getInternalSum(int n) {
return n == 1L ? 0L : (long) n * (long) (n - 1) / 2L;
}
public static class Pair {
public int value;
public int times;
public Pair(int value) {
this.value = value;
this.times = 1;
}
}
public static long communications(int[] arr) {
if (arr == null || arr.length < 2) {
return 0;
}
int size = arr.length;
int maxIndex = 0;
for (int i = 0; i < size; i++) {
maxIndex = arr[maxIndex] < arr[i] ? i : maxIndex;//找到最高山峰的位置
}
int value = arr[maxIndex];//最高山峰的高度
int index = nextIndex(size, maxIndex);//最高山峰的下一个位置
long res = 0L;
Stack
stack.push(new Pair(value));
while (index != maxIndex) {
value = arr[index];
while (!stack.isEmpty() && stack.peek().value < value) {
int times = stack.pop().times;
// res += getInternalSum(times) + times;
// res += stack.isEmpty() ? 0 : times;
res += getInternalSum(times) + times*2;//因为栈底是最大元素,所以在此阶段不可能跳出
}
if (!stack.isEmpty() && stack.peek().value == value) {
stack.peek().times++;
} else {
stack.push(new Pair(value));
}
index = nextIndex(size, index);
}
while (!stack.isEmpty()) {
int times = stack.pop().times;
res += getInternalSum(times);
if (!stack.isEmpty()) {
res += times;
if (stack.size() > 1) {//当栈底还剩大于1个的时候,弹出的那个数还可以与栈底的数称为对数
res += times;
} else {
res += stack.peek().times > 1 ? times : 0;
}
}
}
return res;
}
}
C++版
#include
#include
#include
using namespace std;
struct Pair
{
long value;
long sum;
Pair(long value):value(value),sum(1){}
};
int findindex(int i,int size)
{
return i
int internalsum(Pair a)
{
int n=a.sum;
return n*(n-1)/2;
}
int fun(vector
{
int n=vec.size();
Pair temp(vec[0]);
vector
int max=0;
int maxi=0;
for(int i=1;i
if(vec[i]==vec[i-1])
temp.sum++;
else
{
a.push_back(temp);
if(max
max=temp.value;
maxi=a.size()-1;
}
temp.value=vec[i];
temp.sum=1;
}
}
a.push_back(temp);
if(max
max=temp.value;
maxi=a.size()-1;
}
stack
Pair val=a[maxi];
sta.push(val);
int index=findindex(maxi,a.size());
int count=0;
while(index!=maxi)
{
while(!sta.empty()&&a[index].value>sta.top().value)
{
count+=internalsum(sta.top())+2*sta.top().sum;
sta.pop();
}
if(!sta.empty()&&a[index].value==sta.top().value)
sta.top().sum+=a[index].sum;
else
sta.push(a[index]);
index=findindex(index,a.size());
}
while(!sta.empty())
{
count+=internalsum(sta.top());
int p=sta.top().sum;
sta.pop();
if(!sta.empty())
{
count+=p;
if(sta.size()>1)
count+=p;
else
count+=sta.top().sum>1?p:0;
}
}
return count;
}
int main()
{
int n;
while(cin>>n)
{
vector
int in;
for(int i=0;i
cin>>in;
vec.push_back(in);
}
int result=fun(vec);
cout<
system("pause");
return 0;
}