最详细的主席树(不修改,待修改) BZOJ 1901

By Bartholomew

---

前置知识:

1.树状数组
2.线段树

主席树

模板是干什么的,其实就是询问区间第k大
不支持修改:
复杂度 O(nlogn) O ( n l o g n )
带修:
复杂度 O(n∗(logn)2) O ( n ∗ ( l o g n ) 2 )

分析:

请大家耐心看完下面一道题目的做法,因为跟主席树的关系很大

引题

我们其实有一道题目(现编),就是求一个每次添加元素至末尾的序列的中位数的大小的题目
就相当于给你最后的数组,让你还原每一次的过程中的中位数并依次输出.
(先忽视掉数据范围)
如(样例):

input:
5
4 2 7 3 1
output:
4 (4 序列的中位数)
3 (4 2 的排序后中位数)
4 (4 2 7 排序后的中位数,以此类推)
3.5
3

其中有一个做法就是建立一颗 线段树
每个节点代表一个区间 [i,j] [ i , j ] 意味着离散化后的数字大小为 i i ~ j j 的数字出现了多少次
在我们的样例之中,离散化之后还是只有 5 个数字,所以是建立siz = 5 的树
那么很容易推出这棵树的模样:

那么我们发现当 元素 a[1]=4 a [ 1 ] = 4 (离散化后为4) 加入到这颗树后对每一个节点的影响为以下:

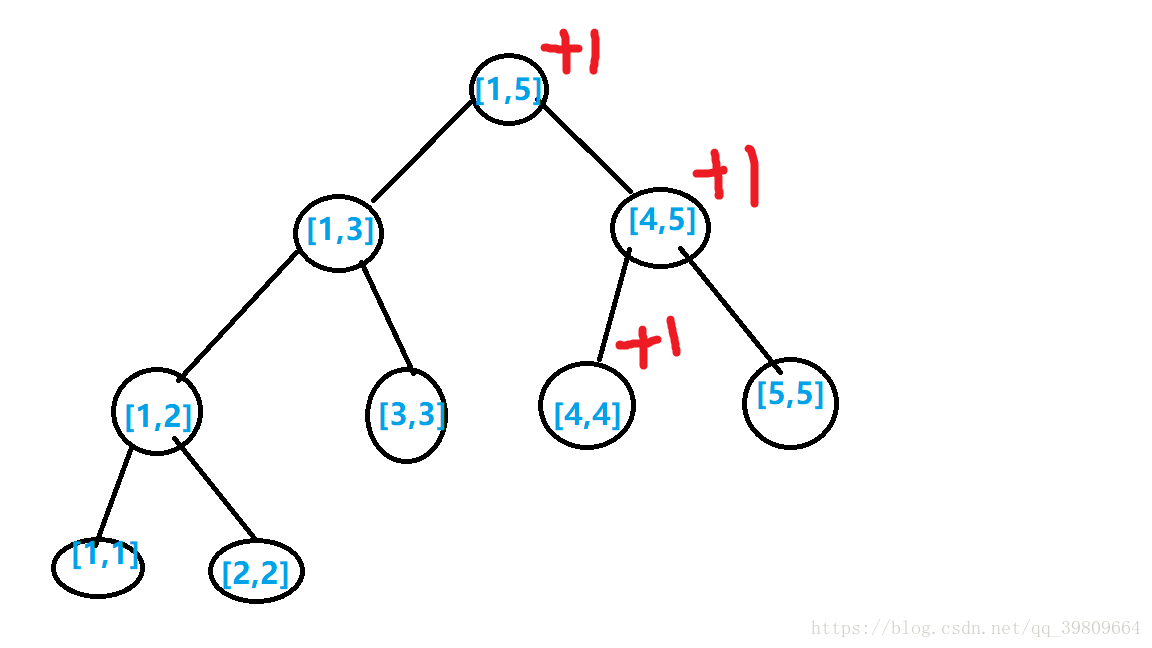
那么我们其实就是知道是怎么加入元素了
但是还有一个问题,就是求 kth k t h 怎么办?
答: 我们可以看 root(指的是当前节点) r o o t ( 指 的 是 当 前 节 点 ) 的左节点,设它的值为 x
如果 x>=k x >= k , 那么就是往下搜索 第 k k 大
如果 x<k x < k , 那么就是往左搜索 第 k−x k − x 大
其实就是一个递归程序,具体细节想必大家都知道的,不必细讲!
那么就可以切入正题了!

解决

我们考虑最暴力的思想:
就是建立 n 棵像上面说的那样的树, 第 i i 棵树 Ti T i 维护的是 区间 [1,i]的序列信息
可以发现,这种树是不是有区间相减的性质?
举个栗子: [3,4] 区间的 离散化大小为 [1,3]的数有多少个? 不就是将T[4] 的 表示 [1,3]区间的节点的权值减去T[2]的节点表示[1,3] 区间的节点的权值就是 [3,4]区间的离散大小为[1,3]的数的个数了吗(前缀思想)
那么这个时间复杂度我们就可以保证是在 nlogn n l o g n 里了,但是我们会发现,每一颗维护区间的树的空间复杂度是不是 O(n) O ( n ) 的,那么随便计算一下发现我们的空间复杂度就是 O(n2) O ( n 2 ) 的了,非常的不爽,怎么办?
但是我们只要观察一下,是不是每一次都是只会有 一条 O(logn) O ( l o g n ) 的路径是被修改的,而别的信息是不是不变的,那么我们就可以考虑每一次只是建立 log 个节点,让这些树共用一些部分
我们翻一下样例:
比如就是一开始我们说的样例好了,假设我们建完了T[3] 这棵树,我们加入第 4 个元素:


那么我们就这样自建立：

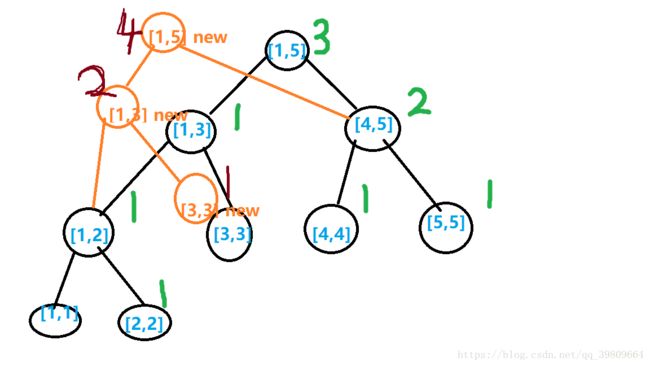
那么我们就是可以保证是没有问题,而且时间与空间复杂度都是稳定的树了

代码:

#pragma GCC optimize(3)
#include 
#include 
#include 
#define N 200005
#define M 4000005
#define R register
using namespace std;

int n, Q, m, cnt, a[N], b[N], x, y, k;
int T[N], ls[M], rs[M], sum[M];

inline int read()
{
    int x = 0;
    char c = getchar();
    bool flag = 0;
    while(c < '0' || c > '9'){if(c == '-')flag = 1;c = getchar();}
    while(c >= '0' && c <= '9'){x = (x << 3) + (x << 1) + (c ^ 48);c = getchar();}
    return flag ? -x : x;
}

int Build(int l, int r)
{
    int now = ++cnt;
    if(l < r)
    {
        int mid = (l + r) >> 1;
        ls[now] = Build(l, mid);
        rs[now] = Build(mid + 1, r);
    }
    return now;
}

inline void Build_new(int mark, int loc)
{
    T[mark] = ++cnt;
    sum[cnt] = sum[T[mark - 1]] + 1;
    int l =  1, r = m, now = cnt, still = T[mark - 1];
    for(; ls[still] || rs[still];)
    {
        int mid = (l + r) >> 1;
        // l ~ mid --- left    mid + 1 ~ r --- right
        if(loc > mid)
        {
            ls[now] = ls[still];rs[now] = ++cnt;
            sum[ rs[now] ] = sum[ rs[still] ] + 1;
            now = rs[now];
            still = rs[still];
            l = mid + 1;
        }
        else
        {
            rs[now] = rs[still];ls[now] = ++cnt;
            sum[ ls[now] ] = sum[ ls[still] ] + 1;
            now = ls[now];
            still = ls[still];
            r = mid;
        }
    }
}

inline int query(int a, int b, int l, int r, int k)
{
    if(l == r) return l;
    int lm = sum[ls[b]] - sum[ls[a]];
    int mid = (l + r) >> 1;
    if(k <= lm) return query(ls[a], ls[b], l, mid, k);
    return query(rs[a], rs[b], mid + 1, r, k - lm);
}

signed main()
{
    n = read(), Q = read();
    for(R int i = 1; i <= n; i++) a[i] = read(), b[i] = a[i];
    sort(b + 1, b + 1 + n);
    m = unique(b + 1, b + 1 + n) - b - 1;
    T[0] = Build(1, m);
    for(R int i = 1; i <= n; i++)
    {
        int loc = lower_bound(b + 1, b + 1 + m, a[i]) - b;
        Build_new(i, loc);
    }
    for(R int i = 1; i <= Q; i++)
    {
        x =read(), y=read(), k=read();
        printf("%d\n", b[query(T[x - 1], T[y], 1, m, k)]);
    }
    return 0;
}

待修主席树

我们现在来思考待修改的主席树

比如这个样例

intput:
5 3
3 2 1 4 7
Q 1 4 3
C 2 6
Q 2 5 3
output:
3
6

Q 表示询问 [x,y] 区间 第 k 大 C 表示将第 x 位的数字修改成为 y

我们不妨想一想对于树状数组的修改是怎么修改的
如果我们暴力的话,其实就是对于 这 T[2] 之后的所有树重新构建一遍,但是显然是不行的对吧!
我们可以考虑只是对于某一些树进行修改

对于更新， 我们不改变这些已经建好的树， 而是另建一批树S，用来记录更新，而这批线段树，我们用树状数组来维护

也就是树状数组的每个节点都是一颗线段树
一开始，S[0]、S[1]、S[2]、S[3]、S[4]、S[5] (建了一棵空树)

就利用树状数组的 lowbit 的性质
将 T[2] 以及 T[2+lowbit(2)] 的之后的所有的树都进行重构 那么 复杂度就是 O(n∗(logn)2) O ( n ∗ ( l o g n ) 2 ) 得到了保证,但是大家可能会有一点疑惑,为什么这样做呢?

请大家记住我说过的话,再重复一遍:
树状数组的每个节点都是一颗线段树,只不过每个点修改都是 O(logn) O ( l o g n ) 的复杂度
因为每颗节点就是一棵树,自然修改就是 log 的复杂度的!

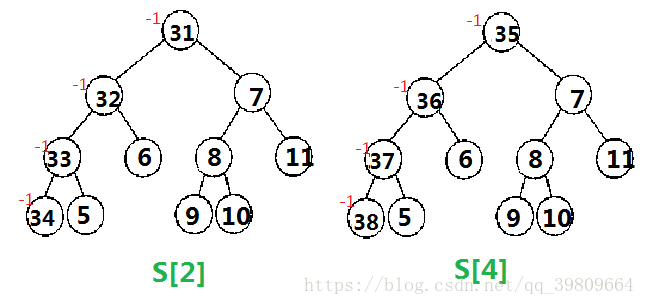
其实我们原来的树状数组代码就是这样的

inline void init()
{
    for(int i=1;i<=n;i++)
        for(int j=i;j<=n;j+=lowbit(j))
            c[j]+=a[i];
}
inline long long get(int x)
{
    int ans=0;
    for(int i=x;i>=1;i-=lowbit(i))
        ans+=c[i];
    return ans;
}

那么我们不要把树状数组想的这么难
就是相当于是我们在询问 某棵树 T[x] 的 某一个位置的节点 k 的真实值罢了
就是 原来的 sum s u m + 修改的 sum s u m
那么 修改的sum 就是 S树 S 树 我们其实就是要看 x,x−lowbit(x) x , x − l o w b i t ( x ) …… 这些树的同样是 k k 的位置的值相加就好了
因为其实我们把树看做一个”点” ,那么我们其实就是问 T[x] 的”真实的样子”,那么我们就是访问 lowbit l o w b i t 的 “点” (就是S 树) 把所有的S树层层叠加得到的树就是 T[x] 的”真实的样子”

Tx,real=Tx+∑i=xi−=lowbit(i)S[i]//把它们当做点来看 T x , r e a l = T x + ∑ i = x i − = l o w b i t ( i ) S [ i ] / / 把 它 们 当 做 点 来 看

那么我们现在不需要问 一整颗树,而是某一个节点,那么我们只要 抓住 位置为询问的节点的点的 sum s u m 值
并把它们相加就是答案了! 对吧!

代码

#pragma GCC optimize(3)
#include 
#include 
#include 
#include 
#define N 60005
#define M 2000005
#define R register
using namespace std;

int n, Q, m, cnt, a[N], b[N], x, y, k;
int T[N], S[N], ls[M], rs[M], sum[M];
int cntE, use[3][N];

struct ques
{
    char s[1];
    int l, r, kth;
}q[N >> 2];
inline int read()
{
    int x = 0;
    char c = getchar();
    bool flag = 0;
    while(c < '0' || c > '9'){if(c == '-')flag = 1;c = getchar();}
    while(c >= '0' && c <= '9'){x = (x << 3) + (x << 1) + (c ^ 48);c = getchar();}
    return flag ? -x : x;
}

int Build(int l, int r)
{
    int now = ++cnt;
    if(l < r)
    {
        int mid = (l + r) >> 1;
        ls[now] = Build(l, mid);
        rs[now] = Build(mid + 1, r);
    }
    return now;
}

inline int Build_new(int flag, int mark, int loc, int val)
{
    int rt = ++cnt; 
    int before;
    if(mark == 1) before = T[0];
    else before = flag ? T[mark - 1] : S[mark - 1];
    if(!flag && val) before = S[mark];
    sum[rt] = sum[before] + val;
    int l =  1, r = m, now = rt, still = before;
    for(; ls[still] || rs[still];)
    {
        int mid = (l + r) >> 1;
        // l ~ mid --- left    mid + 1 ~ r --- right
        if(loc > mid)
        {
            ls[now] = ls[still];
            rs[now] = ++cnt, sum[ rs[now] ] = sum[ rs[still] ] + val;
            now = rs[now];
            still = rs[still];
            l = mid + 1;
        }
        else
        {
            rs[now] = rs[still];
            ls[now] = ++cnt, sum[ ls[now] ] = sum[ ls[still] ] + val;
            now = ls[now];
            still = ls[still];
            r = mid;
        }
    }
    return rt;
}

inline int lowbit(int x) { return x & (-x); }
inline int Sum(int y, int x)
{
    int res = 0;
    for(R int i = x; i >= 1; i -= lowbit(i))
        res += sum[ls[use[y][i]]];
    return res;
}
inline int query(int u, int v, int a, int b, int l, int r, int k)
{
    if(l == r) return l;
    int lm = Sum(2, v) + sum[ls[b]] - sum[ls[a]] - Sum(1, u);
    int mid = (l + r) >> 1;
    if(k <= lm) 
    {
        for(R int i = u; i >= 1; i -= lowbit(i))
            use[1][i] = ls[use[1][i]];
        for(R int i = v; i >= 1; i -= lowbit(i))
            use[2][i] = ls[use[2][i]];
        return query(u, v, ls[a], ls[b], l, mid, k);
    }
    for(R int i = u; i >= 1; i -= lowbit(i))
            use[1][i] = rs[use[1][i]];
    for(R int i = v; i >= 1; i -= lowbit(i))
            use[2][i] = rs[use[2][i]];
    return query(u, v, rs[a], rs[b], mid + 1, r, k - lm);
    return 0;
}

inline void update(int loc,int num)
{
    int where;
    where = lower_bound(b + 1, b + 1 + m, a[loc]) - b;
    for(R int i = loc; i <= n; i += lowbit(i))
        S[i] = Build_new(0, i, where, -1);
    where = lower_bound(b + 1, b + 1 + m, num) - b;
    for(R int i = loc; i <= n; i +=lowbit(i))
        S[i] = Build_new(0, i, where, 1);
    a[loc] = num;
}

signed main()
{
    n = read(), Q = read();
    for(R int i = 1; i <= n; i++) a[i] = read(), b[i] = a[i];
    cntE = n;
    for(R int i = 1; i <= Q; i++)
    {
        scanf("%s%d%d", q[i].s, &q[i].l, &q[i].r);
        if(q[i].s[0] == 'Q')
            scanf("%d", &q[i].kth);
        else 
            b[++cntE] = q[i].r;
    }
    sort(b + 1, b + 1 + cntE);
    m = unique(b + 1, b + 1 + cntE) - b - 1;
    T[0] = Build(1, m);
    for(R int i = 1; i <= n; i++)
    {
        int loc = lower_bound(b + 1, b + 1 + m, a[i]) - b;
        T[i] = Build_new(1, i, loc, 1);
    }
    for(R int i = 1; i <= n; i++)
        S[i] = Build_new(0, i, 1, 0);
    for(R int i = 1; i <= Q; ++i)
    {
        if(q[i].s[0] == 'Q')
        {
            int x = q[i].l, y = q[i].r;
            for(R int j = x - 1; j >= 1; j -= lowbit(j))
                use[1][j] = S[j];
            for(R int j = y; j >= 1; j -= lowbit(j))
                use[2][j] = S[j];
            printf("%d\n", b[query(x - 1, y, T[x - 1], T[y], 1, m, q[i].kth)]);
        }
        else
            update(q[i].l, q[i].r);
    }
    return 0;
}