左神算法课程笔记PART1:二分、排序、栈、队列、矩阵、链表、二叉树
文章目录
- 福利课
- 二分答案
- 初级班
- lesson1
- lesson2 排序
- lesson3 栈、队列、矩阵
- lesson4 链表
- lesson4 二叉树
PS:笔记并不全,只记录我感觉需要记录的。
福利课
在数组中找到一个局部最小的位置
方法:
二分答案
二分策略和有序无关,而和0 1标准有关。进行二分时,只需要保证一边有答案,另一边无答案,或一边可能有,另一边绝对没有。只要有这样的标准,都能二分!
初级班
lesson1
1.对数器:https://blog.csdn.net/weixin_39953502/article/details/79504879
2.master公式:

3.TIP
关于取中间值为什么为l+(r-l)/2,而不是(l+r)/2
4.归并排序
思想:小范围有序在合并为大范围有序时,不会浪费小范围内已经进行过的的比较,因为小范围内已经有序。O(n²)复杂度的排序会重复多次已经进行过的比较。
所以很多O(n^2)复杂度需要比较的算法,可以用归并思想改善。
【非递归】bottom-to-up 的归并思路是这样的:先两个两个的 merge,完成一趟后,再 4 个4个的 merge,直到结束。
例题:
1)小和问题:在一个数组中,每一个数左边比当前数小的数累加起来,叫做这个数组的小和。求一个数组的小和。
2)逆序对:在一个数组中,左边的数如果比右边的数大,则折两个数构成一个逆序对,请打印所有逆序对。
lesson2 排序
1.快排:
1)荷兰国旗问题:
public static int[] partition(int[] arr, int L, int R, int p) {
int less = L - 1;
int more = R + 1;
while (L < more) {
if (arr[L] < p) {
swap(arr, ++less, L++);
} else if (arr[L] > p) {
swap(arr, --more, L);
} else {
L++;
}
}
return new int[] { less + 1, more - 1 };
}
2)用荷兰国旗问题改进快排:
一次划分排序的元素数量>=1(包括重复元素)。
public static void quickSort(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
quickSort(arr, 0, arr.length - 1);
}
public static void quickSort(int[] arr, int L, int R) {
if (L < R) {
//swap(arr, L + (int) (Math.random() * (R - L + 1)), R);
int[] p = partition(arr, L, R);
quickSort(arr, L, p[0] - 1);
quickSort(arr, p[1] + 1, R);
}
}
public static int[] partition(int[] arr, int l, int r) {
int less = l - 1;
int more = r;
while (l < more) {
if (arr[l] < arr[r]) {
swap(arr, ++less, l++);
} else if (arr[l] > arr[r]) {
swap(arr, --more, l);
} else {
l++;
}
}
swap(arr, more, r);
return new int[] { less + 1, more };
}
public static void swap(int[] arr, int i, int j) {
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}
3)快排空间复杂度O(lgN):需要定义变量来保存划分点,期望的变量数为O(lgN)。
4)工程上的快排都是非递归:递归浪费的空间、时间可以通过改为非递归版本来避免。(工程上几乎没有递归)
2.堆排序:
void heapify(int arr[], int heapsize, int i)
{
int largest = i; // Initialize largest as root
int l = 2*i + 1; // left = 2*i + 1
int r = 2*i + 2; // right = 2*i + 2
if (l < heapsize && arr[l] > arr[largest])
largest = l;
if (r < heapsize && arr[r] > arr[largest])
largest = r;
if (largest != i)
{
swap(arr[i], arr[largest]);
heapify(arr, heapsize, largest);
}
}
void bulid_max_heap(int arr[], int heapsize)
{
for(int i = heapsize / 2 - 1; i >= 0; i--)
heapify(arr,heapsize,i);
}
void HeapSort(int arr[], int heapsize)
{
bulid_max_heap(arr,heapsize);
for(int i = heapsize - 1; i >= 0; i--)
{
swap(arr[0],arr[i]);
heapify(arr,i,0);
}
}
1)数据流中位数问题:(用两个堆划分数组)
建立一个大根堆和一个小根堆,将数据流输出的数加入两个堆中(比大根堆堆顶小的放入大根堆,比小根堆堆顶大的放入小根堆),同时维持两个堆大小之差不超过1,中位数就在两个堆顶产生。
2)几乎有序数组排序
已知一个几乎有序的数组,几乎有序是指,如果把数组排好顺序的话,每个元素移动的距离可以不超过k,并且k相对于数组来说比较小。请选择一个合适的排序算法针对这个数据进行排序。
【思路】堆排序:把前k+1个数放进大小为k+1的小根堆中,弹出堆顶,必为最小值放在a[0]处。然后往右每加一个数,弹出一个数,排序依次完成。
4.排序补充:
工程上排序:内置类型排序用快排,自定义类型排序用归并排序(稳定),size<60用插入排序(常系数非常小,数量少时有优势)。
5.比较器:
//降序
bool cmp_down(int a, int b)
{
return a>b;
}
//升序
bool cmp_up(int a, int b)
{
return a<b;
}
符合排序规则才返回true,其他情况均返回fasle!
6.桶排序
7.最大间隙问题
lesson3 栈、队列、矩阵
1.用数组结构实现栈和队列
2.可以实现返回最小元素功能的栈
3.队列实现栈,栈实现队列
4.猫狗队列
矩阵问题:
5.转圈打印矩阵
6.旋转正方形
方法一:矩阵\正方形问题一种思路:把矩阵分为一圈一圈,从外向内依次处理每一圈。以每一圈的左上顶点和右下顶点的坐标作为参数定位这个圈。
方法二:先转置,再竖轴镜像反转
7.之字形打印矩阵:
定义两个点变量,一个往右一个往下,每次打印两点连线经过的所有点。
8.在行列都排好序的矩阵中找数:
从右上顶点往左遍历,比该点小往左,比该点大往下。
PS:一道题目最优解来自数据状况或者它的问法
lesson4 链表
链表笔记
1.将单向链表按某值划分成左边小、中间相等、右边大的形式,要求每一部分节点相对顺序不变,且额外空间O(1),时间O(n).
【思路】额外新建三个节点,分别存放的是小于pivot ,等于pivot ,大于pivot 。每个节点需要保存头head和尾tail,每次增加一个节点都需要tail++,最后链接所有的头和位。注意要判断头尾是否为空,因为可能三部分有的为空。
2.两个单链表相交的一系列问题(最难!)
步骤:(loop1为第一个链表的入环节点,loop2为第二个链表入环节点)
1.判断是否有环:
1)方法一:利用hashset对两个单链表进行遍历,判断链表中的数值再hashset中是否存在,存在则有环,不存在则无环。
2)方法二:不用哈希表的话需要准备两个指针,快指针和慢指针,快指针一次走两步,慢指针一次走一步,如果有环,则快指针和慢指针一定会在环上相遇。快指针和慢指针相遇之后,将快指针调整到链表开始,此时快指针和慢指针均按一次一步,则会再第一个入环节点相遇。
2.判断是否相交:
1)两个链表都无环
①方法一:则将链表1所有节点放入map中,遍历链表2,查找map,是否在map中存在,需要额外空间O(n)。
②方法二:不使用map则先遍历map1,得到链表1的长度及链表1的最后一个节点。再遍历链表2的长度,及链表2的最后一个节点。如果end1跟end2相等,则比较链表长度,多的部分让多的链表先走多的部分,之后两个链表同时走,最终会走到首次相交的地方,O(1)空间。
2)单链表结构一个有环一个无环不可能相交。
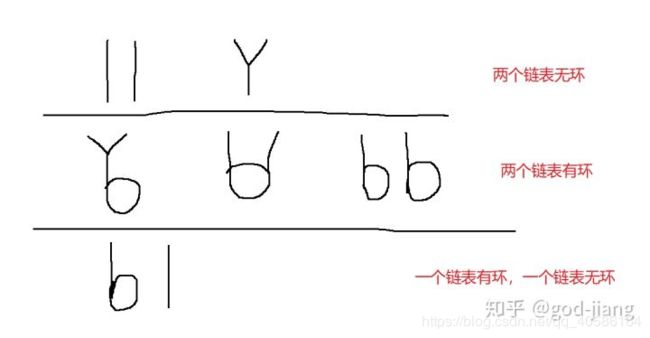
3)有环的拓扑结构只可能有三种情况:如图所示。
loop1,loop2,head1,head2就足够区分开三种情况.
①loop1等于loop2,则为情况1,砍掉环的部分,则又转化为之前的无环链表结构。
②loop1不等于loop2,则为情况2或情况3。
a.情况2:如果loop1在遍历过程中遇到了loop2,则相交,返回loop1或loop2皆可。
b.情况3:loop1接着往下走,如果loop1往下走没遇见loop2,则不相交。
lesson4 二叉树
1.三种遍历
2.福利树(直观打印二叉树)
从左往右对应从上往下层数,箭头表示父节点的位置(^表示父节点在左上方)。
3.寻找后继节点
4.二叉树的序列化和反序列化
5.折纸问题
实际上是一个二叉树,每次折叠会在上次每个叠痕上方多一个向下叠痕,下方多一个向上叠痕,就是一个满二叉树,每一个节点左子树的根为下,右子树的根为上。中序遍历该满二叉树即可。
6.判断一颗二叉树是否为平衡二叉树
PS:递归函数处理二叉树很好用,因为一个点在递归中会出现三次,并且带着左右子树的信息(第一次遍历、左子树遍历完回到该点、右子树遍历完回到该点),树型DP。
7.判断一棵树是否为搜索二叉树:搜索二叉树中序遍历顺序为升序,中序遍历即可。
完全二叉树:层次遍历完全二叉树需要满足下面两个条件
- 如果有右孩子,必有左孩子,否则返回false;
- 如果该节点没有右孩子(叶节点或有左没右),那后面的节点都是叶节点,否则返回false.
8.时间复杂度低于O(n)求完全二叉树的节点个数
递归思路:先从一直向左遍历到底部求出树高度h,再从右节点开始一直向左求出右子树高度:
如果右子树高度=h-1,说明左子树为高度h-1的满二叉树,可得左子树节点个数,递归得到右子树节点个数;如果右子树高度=h-2,说明右子树为高度为h-2的满二叉树,递归得到左子树节点个数。