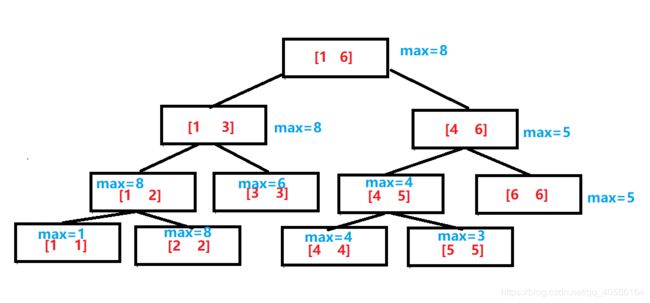
线段树模板

使用场景

O(n)时间初始化(建树)，O(logn）时间内完成区间查询、区间(或单点)更新。

主要解决区间 动态 修改&查询 问题（查询区间最值、区间和……）。

模板

简约版

不需要区间更新，最多单点更新，不需要lazy标记。
求区间和：

#include 
using namespace std;
const static int N = 100010;  //数组大小
typedef long long ll;
ll A[N], tree[4 * N];
//将处理好的左右儿子节点的值更新给父节点
void pushUp(int rt) {
    tree[rt] = tree[rt << 1] + tree[rt << 1 | 1];
}

//当前根节点rt对应的原数组区间为[l,r],rt以1为起始
void build(int rt, int l, int r) {
    if (l == r) {
        tree[rt] = A[r];
        return;
    }
    int mid = (l + r) >> 1;
    build(rt << 1, l, mid);
    build(rt << 1 | 1, mid + 1, r);
    pushUp(rt);
}
//单点修改，将A[pos]的值修改为val
void update(int rt, int l, int r, int pos, int val) {
    if (l == r) {
        A[pos] = val;
        tree[rt] = val;
        return;
    }
    int mid = (l + r) >> 1;
    if (pos <= mid)
        update(rt << 1, l, mid, pos, val);
    else
        update(rt << 1 | 1, mid + 1, r, pos, val);
    pushUp(rt);
}

// 查询区间[start,end]的和
ll rangeQuery(int rt, int l, int r, int start, int end) {
    if (start <= l && end >= r)
        return tree[rt];
    int mid = (l + r) >> 1;
    ll res = 0;
    if (start <= mid)
        res += rangeQuery(rt << 1, l, mid, start, end);
    if (end >= mid + 1)
        res += rangeQuery(rt << 1 | 1, mid + 1, r, start, end);
    return res;
}

int main() {
    vector<int> arr = {1, 3, 5, 2, 4};
    int n = arr.size();                       //区间大小
    for (int i = 1, j = 0; i <= n; i++, j++)  //从A[1]开始输入，忽略A[0]
        A[i] = arr[i - 1];
    build(1, 1, n);
    cout << rangeQuery(1, 1, 5, 2,5) << endl;
    update(1, 1, 5, 5, 0);
    cout << rangeQuery(1, 1, 5, 2, 5) << endl;
    getchar();
    return 0;
}

完全版

区间更新，有lazy标记。
求区间和：

#include 
using namespace std;
const static int N = 100010;  //数组大小
typedef long long ll;
ll A[N], tree[4 * N], tag[4 * N];
//将处理好的左右儿子节点的值更新给父节点
void pushUp(int rt) {
    tree[rt] = tree[rt << 1] + tree[rt << 1 | 1];
}
//将父节点的tag信息传递给两个孩子节点,[l,r]为节点rt区间
void pushDown(int rt, int l, int r) {
    if (tag[rt] != 0) {
        int mid = (l + r) >> 1;
        ll lazy = tag[rt];
        tree[rt << 1] += (mid - l + 1) * lazy;
        tree[rt << 1 | 1] += (r - mid) * lazy;
        tag[rt << 1] += lazy;
        tag[rt << 1 | 1] += lazy;
        tag[rt] = 0;
    }
}
//当前根节点rt对应的原数组区间为[l,r],rt以1为起始
void build(int rt, int l, int r) {
    if (l == r) {
        tree[rt] = A[r];
        return;
    }
    int mid = (l + r) >> 1;
    build(rt << 1, l, mid);
    build(rt << 1 | 1, mid + 1, r);
    pushUp(rt);
}
//将区间[start,end]的值都加上delta,[l,r]为节点rt区间
void updateRange(int rt, int l, int r, int start, int end, ll delta) {
    if (start <= l && end >= r) {
        tree[rt] += (r - l + 1) * delta;
        tag[rt] += delta;
        return;
    }
    pushDown(rt, l, r);
    int mid = (l + r) >> 1;
    if (start <= mid)
        updateRange(rt << 1, l, mid, start, end, delta);
    if (end >= mid + 1)
        updateRange(rt << 1 | 1, mid + 1, r, start, end, delta);
    pushUp(rt);
}
// 查询区间[start,end]的和,[l,r]为节点rt区间
ll rangeQuery(int rt, int l, int r, int start, int end) {
    if (start <= l && end >= r)
        return tree[rt];
    pushDown(rt, l, r);
    int mid = (l + r) >> 1;
    ll res = 0;
    if (start <= mid)
        res += rangeQuery(rt << 1, l, mid, start, end);
    if (end >= mid + 1)
        res += rangeQuery(rt << 1 | 1, mid + 1, r, start, end);
    return res;
}
int main() {
    vector<int> arr={1,3,5,2,4};
    int n=arr.size();  //区间大小
    for (int i = 1,j=0; i <= n; i++,j++)//从A[1]开始输入，忽略A[0]
        A[i]=arr[i-1];
    build(1, 1, n);
    cout<<rangeQuery(1,1,5,2,4)<<endl;
    updateRange(1,1,5,2,2,1);
    cout<<rangeQuery(1,1,5,2,4);
    getchar();
    return 0;
}

参考：
https://www.cnblogs.com/xenny/p/9801703.html
https://www.acwing.com/blog/content/514/