(七)1.1_普里姆算法求无向连通网的最小生成树

注意:本算法使用的是邻接表来存储图

一.普里姆算法

  以一个起点为连通分量(这里以v1为起点),从其他未连接至该连通分量的顶点中找出一个顶点,该顶点连接该连通分量的最短边是所有未连接到该连通分量中的边中最短的,然后连接该顶点,然后继续从其他未连接至该连通分量的顶点中找出一个顶点,重复上述步骤n次(n=顶点数-1)…最后所有顶点都被连接,求出了最小生成树

二.思路分析

  1.我们要构建一个辅助数组closeedge[ ],用来记录顶点连接至连通分量的最短边

  2.初始时我们以一个起点为连通分量,这里使起点的最短边权值记为0,表示已连接至连通分量,然后计算各个未连接顶点到该连通分量的最短边的权值并记录到辅助数组closeedge[ ]中

  3.接着我们从辅助数组closeedge[ ]数组中找到一个顶点到连通分量的最短边(权值非0,权值为0表示已连接)是所有未连接到连通分量中的边中最短的,然后就将顶点连接至连通分量,然后将该条最短边权值赋为0,表示已连接(这里如何从数组中找到最短边用的是类似于选择排序的算法)

  4.然后我们要遍历依附于刚刚连接的顶点的边,检查一下是否改变了那些未连接顶点的最小边,如过最短边变短了,就覆盖更新(因为连通分量增加了一个顶点,可能其他未连接的顶点连接该顶点的边比原来的最短边更短)
  就这样重复3.4步骤,直到所有顶点都被连接

三.代码实现

#include"stdio.h"
#include"stdlib.h"
#define MAX_VERTEX_NUM 50   //最大顶点数 
#define NOWAY 9999999    //没有路径权值无穷大 
 
typedef int VertexType;     //顶点类型(顶点的值) 
typedef int VRType;         //顶点关系类型(权值) 
 	
typedef enum
{
  DG,DN,UDG,UDN		    //{有向图,有向网,无向图,无向网}
}GraphKind;         //图类型 

typedef struct ArcNode
{
	int adjvex;                   //该弧所指向的顶点的位置(顺序表中的位置)
	int weight;                   //弧的权值(无权值的图用1表示连通,有权值的图就是直接存入权值) 
	struct  ArcNode *nextarc;	  //指向下一条弧的指针 
	//InfoType *info;     //该弧相关信息的指针
}ArcNode;    //弧 

typedef struct VNode
{
  VertexType data;          //顶点信息(顶点的值)  
  ArcNode *firstarc;	    //指向第一条依附该顶点弧的指针 
}VNode;    //顶点

typedef struct
{
   VNode vexs[MAX_VERTEX_NUM];                  //顶点向量顺序表
   int vexnum,arcnum;                           //图的当前顶点数和弧数
   GraphKind kind;                              //图的种类标志	  
}ALGraph;  //邻接表图 

//搜寻顶点在顺序表中的位置 
int LocateVex(ALGraph &G,VertexType v)
{
	for(int pos=0;pos<G.vexnum;pos++)
	{
		if(G.vexs[pos].data==v)
		  return pos;
	}
	return 0;
}
 //构建无向图 
void CreateNDG(ALGraph &G)
{
	printf("\n请依次输入无向图的顶点数和边数(空格隔开):\n"); 
    scanf("%d %d",&G.vexnum,&G.arcnum);     //输入图的顶点数和弧数
    
    printf("\n请依次输入无向图的顶点向量(空格隔开)\n"); 
    for(int pos=0;pos<G.vexnum;pos++)
	   {
	    scanf("%d",&G.vexs[pos].data);         //输入图的顶点向量
	    G.vexs[pos].firstarc=NULL;             //第一条弧的指针暂时赋为空 
	   }
	
	printf("\n请依次输入无向图的边依附的两个顶点与权值(空格隔开,按回车输入下一条边):\n"); 
	VertexType v1,v2;        //边依附的顶点 
	VRType w;                //的权值 
	int head,tail;           //顶点在顺序表中的位置序号    	
	for(int a=0;a<G.arcnum;a++)
	{		
		scanf("%d %d %d",&v1,&v2,&w);     //输入边依附的两个顶点与权值 
		head=LocateVex(G,v1);            //找到顶点在顺序表中的位置 
		tail=LocateVex(G,v2);            //找到顶点在顺序表中的位置
		//第一个节点 
		ArcNode *node=(ArcNode*)malloc(sizeof(ArcNode));    //新建边节点 
		node->weight=w;
		node->adjvex=tail;
		node->nextarc=G.vexs[head].firstarc;      //用前插法将边节点插入 
		G.vexs[head].firstarc=node;
		
		//第二个节点 
		ArcNode *node2=(ArcNode*)malloc(sizeof(ArcNode));    //新建边节点 
		node2->weight=w;
		node2->adjvex=head;
		node2->nextarc=G.vexs[tail].firstarc;      //用前插法将边节点插入 
		G.vexs[tail].firstarc=node2; 
	}   
}
//普里姆算法求无向连通网的最小生成树 
void MiniSpanTree_PRIM(ALGraph &G,VertexType u)
{
   struct 
   {
   	VertexType adjvex;  //顶点 
	int lowcost;	   //权值 		
   }closeedge[G.vexnum];    //最短边 
   
   int s=LocateVex(G,u);          //找到起点顶点在顺序表中的位置	
   for(int j=0;j<G.vexnum;j++)    //辅助数组初始化表示顶点未连接,j对应顶点在顺序表中的位置 
	  closeedge[j]={u,NOWAY};	
   for(ArcNode *p=G.vexs[s].firstarc;p!=NULL;p=p->nextarc)      //依次遍历起点u的邻接顶点
   	  closeedge[p->adjvex]={u,p->weight};		//更新这些顶点的最短边
   closeedge[s].lowcost=0;         //初始,U={v} 
     
   for(int j=1;j<G.vexnum;j++)     //选择其余G.vexnum-1个顶点,j对应顶点在顺序表中的位置  
   {
   	   //求最小边算法 
       int k;	   
	   for(k=-1;k<G.vexnum;)       //找到一个没有被连接的顶点的位置序号,k对应顶点在顺序表中的位置  
	   {
		  if(closeedge[++k].lowcost!=0)
			 break;
	   } 
	   for(int pos=k+1;pos<G.vexnum;pos++)           //遍历最小边数组	   	
		  k=(closeedge[pos].lowcost<closeedge[k].lowcost&&closeedge[pos].lowcost!=0)?pos:k;     //找出最小边对应顶点的位置序号 
	   //求最小边算法 
	   	
   	   printf("连接v%d-v%d,权值=%d\n",closeedge[k].adjvex,G.vexs[k].data,closeedge[k].lowcost); 
   	   closeedge[k].lowcost=0;         //第k顶点并入U集
	
	  //新顶点并入U后观察新顶点依附的边是否有比原来的最小边更小 
	    for(ArcNode *p=G.vexs[k].firstarc;p!=NULL;p=p->nextarc)      //依次遍历邻接顶点
       {
  	     if(p->weight<closeedge[p->adjvex].lowcost)               //如果比原来的最小边更小 
   	     closeedge[p->adjvex]={G.vexs[k].data,p->weight};        //覆盖更新最短边	
       }//for p	     	    	
   }//for j
}//MiniSpanTree_PRIM

int main()
{	
	ALGraph G2;
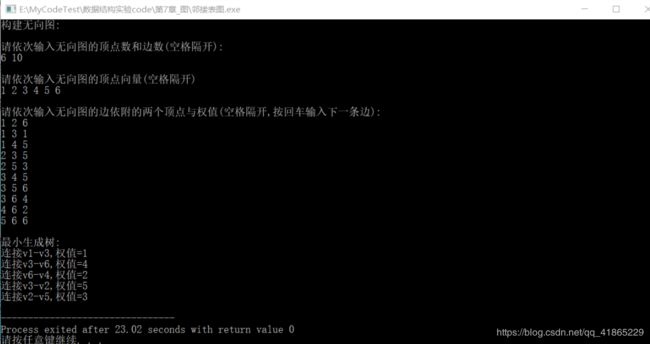
    printf("\n构建无向图:\n");
	CreateNDG(G2); 
    printf("\n最小生成树:\n"); 
	MiniSpanTree_PRIM(G2,1); 	
	return 0;
}

操作结果: