Educational Codeforces Round 90 (Rated for Div. 2) CF1373 E,F,G题解

E:

首先考虑第一位的$f()=m$,枚举m，后面的k个的$f()$为$(m+1,m+2,m+3...m+k)$（不考虑进位）。
对于这些m，直接贪心选择数:越靠后的数字尽可能大。
如果要进位，最多只可能进一次，也就变成了:
$m,m+1,m+2,m+3...m+i-j\ast 9...m+k-j\ast 9$
对于这类情况直接枚举进位的个数就行了。
代码:
$O(n^3)$

#include
#define rb(a,b,c) for(int a=b;a<=c;++a)
#define rl(a,b,c) for(int a=b;a>=c;--a)
#define LL long long
#define IT iterator
#define PB push_back
#define II(a,b) make_pair(a,b)
#define FIR first
#define SEC second
#define FREO freopen("check.out","w",stdout)
#define rep(a,b) for(int a=0;a
#define KEEP while(1)
#define SRAND mt19937 rng(chrono::steady_clock::now().time_since_epoch().count())
#define random(a) rng()%a
#define ALL(a) a.begin(),a.end()
#define POB pop_back
#define ff fflush(stdout)
#define fastio ios::sync_with_stdio(false)
#define debug_pair(A) cerr<
using namespace std;
const LL INF=1e18;
typedef pair<int,int> mp;
typedef pair<mp,mp> superpair;
#define int LL
int n,k;
int check(int num){
//	int cnt=0;
	if(num%9==0){
		return num/9; 
	}
	return 0;//
//	while(num){
//		if(num%10==9) cnt++;
//		else{
//			return 0;
//		}
//		num/=10;
//	}
//	return cnt;
}
int check2(int num,int k){
	int res=0;
	rb(i,num,num-1+k){
		int tmp=i;
		while(tmp){
			res+=tmp%10;
//			cout<
			tmp/=10;
		}
//		cout<
	}
	return res;
}
string Min(string s1,string s2){
	if(s1==":"){
		return s2;
	}
	else{
		if(s1.length()<s2.length()){
			return s1;
		}
		if(s1.length()>s2.length()){
			return s2;
		}
		return min(s1,s2);
	}
}
void solve(){
	cin>>n>>k;
	string res=":";
	k++;
	rb(i,0,n){
		int save=n;
		n-=(k*(i+i+k-1))/2;
		if(n>0){
			n=save;
			continue;
		}
		if(n==0){
			LL base=1;
			string tmp="";
			int rest=i;
			while(rest){
				if(rest+k-1<10&&base==1){
					tmp+=char('0'+rest);
					rest=0;
					break;
				}
				if(base==1){
					tmp+=char('0'+9-k+1);
					base*=10;
					rest-=9-k+1;				
				}
				else{
					tmp=char('0'+min(9ll,rest))+tmp;
					base*=10;
					rest-=min(9ll,rest);
				}
//					cout<
			}
			if(tmp==""){
				tmp="0";
			}
			res=Min(res,tmp);
		}
		else{//
//			if(i==23){
//				cout<
//			} 
			n=-n;
			rb(j,1,n-1){
				if(j>k-1) continue;
				if(n%j==0&&check(n/j)){
					int tmp=check(n/j);
					tmp--;
					int fi=k-j;
					fi--;
					int rest=i;
					rest-=tmp*9;
					rest-=9-fi;
					if(rest>=0){
						LL base=10;
						string tt="";
						tt+=char('0'+9-fi);
						rb(I,1,tmp){
							tt='9'+tt;
							base*=10;
						}
						bool ok=1;
						while(rest){
							tt=char('0'+min(rest,9ll-ok))+tt;
							rest-=min(rest,9ll-ok);
							base*=10;
							ok=0;
						}
						res=Min(res,tt);
					}
				}
			}
		}
		n=save;
	}	
	
	if(res[0]==':'){
		res="-1";
	}
	cout<<res<<endl;
}
signed main(){
	fastio;
	int t;
	cin>>t;
	while(t--) solve();
	return 0;
}
/*
1
123 2

1
26 4
896 897 898 899 900
*/

F:

两种做法:

第一种：

类似于"HMT"如果连续的一段基站的值<他们之间的房子的需要值则不可以，否则ok。
可以看一下这个证明。

第二种

假设第1个基站分给了第一个城市里的$x$个房子的网。
那么剩下的那么多怎么分配？
首先贪心考虑，由于 第一个基站分给了第一个城市$x$个则剩下$b_1-x$个，由于这些只能分给第2个城市了则就把它们全部分给第二个城市。设第$i$房子还需要的值位$nee{d}_i$。这样$nee{d}_2=nee{d}_2-(b[1]-x)$…也就是对于基站$i(i\ge 2)$，先补完前面一个，然后把所有的都分给后面的一个。
这样也就是只要固定了$x$最优的策略也就固定了。
设$f(x)$表示如果给第一个基站分给第一个城市x个之后，为了满足所有的城市，还差$f(x)$个。
显然如果存在一个$x(0\le x\le min(a_1,b_1),f(x)=0)$,则答案位$YES$,否则位$NO$.。
显然如果第一个基站给第一个城市$x$个后。

• 如果$x$给多了，那么$f(x)\le f(x+1)\le f(x)+1$也就是$f(x),f(x+1)......f(min(a_1,b_1))$是递增的
• 如果$x$给少了，那么$f(x)\le f(x-1)\le f(x)+1$也就是$f(x),f(x-1)......f(0)$是递增的。

则是一个这样的图像:

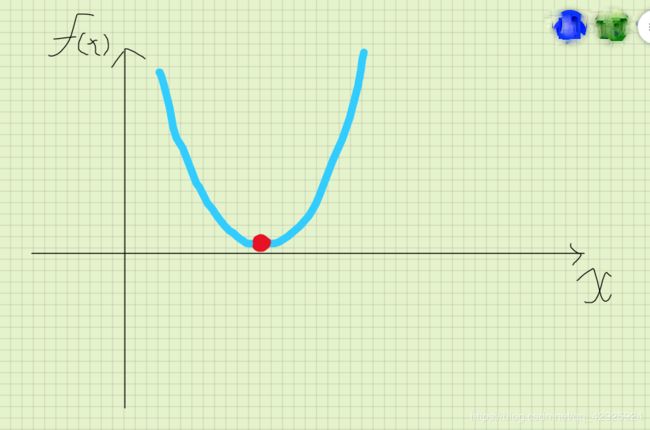
那么只要这个红点(最低点)在x轴上则答案为$YES$
code:
$O(nlogn)$

#include
#define rb(a,b,c) for(int a=b;a<=c;++a)
#define rl(a,b,c) for(int a=b;a>=c;--a)
#define LL long long
#define IT iterator
#define PB push_back
#define II(a,b) make_pair(a,b)
#define FIR first
#define SEC second
#define FREO freopen("check.out","w",stdout)
#define rep(a,b) for(int a=0;a
#define KEEP while(1)
#define SRAND mt19937 rng(chrono::steady_clock::now().time_since_epoch().count())
#define random(a) rng()%a
#define ALL(a) a.begin(),a.end()
#define POB pop_back
#define ff fflush(stdout)
#define fastio ios::sync_with_stdio(false)
#define debug_pair(A) cerr<
using namespace std;
const int INF=0x3f3f3f3f;
typedef pair<int,int> mp;
typedef pair<mp,mp> superpair;
int tmp[1000000+2],n,a[1000000+2],b[1000000+2];
LL check2(int x)
{
	rb(i,1,n){
		tmp[i]=a[i];
	}
	tmp[1]-=x;
	LL res=0;
	rb(i,2,n){
		int rest=b[i-1];
		if(i!=2)rest-=tmp[i-1];
		else rest-=x;
		if(rest<0){
			res+=-rest;
//			cerr<
			rest=0;
		}
		tmp[i]-=min(tmp[i],rest);
	}
//	cerr<
	res+=max(0,tmp[1]+tmp[n]-b[n]);
//	cerr<<"#"<
	return res;
}
bool check(int x){
	return check2(x-1)>=check2(x);
}
void mian(){
	bool ok=1;
	cin>>n;
	rb(i,1,n)
		cin>>a[i];
	rb(i,1,n)
		cin>>b[i];
//	check2(1);
//	return ;
	if(check2(0)){
		int l=1,r=min(b[1],a[1])+1;
		while(l<r-1){
			int mid=(l+r)>>1;
			if(check(mid)){
				l=mid;
			}
			else{
				r=mid;
			}
		}
//		cerr<<"#"<
		if(check2(l)){
			ok=0;
		}
	}
	cout<<(ok? "YES":"NO")<<endl;	
}
int main(){
	fastio;
	int t;
	cin>>t;
	while(t--){
		mian();
	}
	return 0;
}
/*
10
2 3 2 1 1 6 3 9 2 1
1 2 1 3 8 5 8 7 2 3
*/

G

首先可以贪心如果一个数在(x,y)要走到k列则，至少要走到$(k,y+|k-x|)$这样可以给每一个在棋盘上的棋子附上一个士兵(x,y) 一个$val=y+|k-x|$也就是至少走到的行数。
把所有val从小到大排序:
$$va{l}_1,va{l}_2,va{l}_3...va{l}_m$$
由于每一个格子最多有一个士兵，所以在纸上推一下就可以发现如果把每一个数$va{l}_i$加上$m-i$:
$$va{l}_1+m-1,va{l}_2+m-2,va{l}_3+m-3...va{l}_m+0$$
答案就是：
$$max(0,max(va{l}_1+m-1,va{l}_2+m-2,va{l}_3+m-3...va{l}_m+0)-n)$$
维护这个东西可以用fhq-treap,非常方便
code:
$O(mlogm)$

#include
#define rb(a,b,c) for(int a=b;a<=c;++a)
#define rl(a,b,c) for(int a=b;a>=c;--a)
#define LL long long
#define IT iterator
#define PB push_back
#define II(a,b) make_pair(a,b)
#define FIR first
#define SEC second
#define FREO freopen("check.out","w",stdout)
#define rep(a,b) for(int a=0;a
#define KEEP while(1)
//#define SRAND mt19937 rng(chrono::steady_clock::now().time_since_epoch().count())
#define random(a) rand()%a
#define ALL(a) a.begin(),a.end()
#define POB pop_back
#define ff fflush(stdout)
#define fastio ios::sync_with_stdio(false)
#define debug_pair(A) cerr<
using namespace std;
//const LL INF=23333333333333333;
typedef pair<int,int> mp;
typedef pair<mp,mp> superpair;
struct node{
int maxi,add,val,block;
int size,l,r,fix;
bool flag;
}v[200000+20];
void update(int index)
{
//	v[index].mini=v[index].block;
	v[index].maxi=v[index].val;
	v[index].size=1;
	if(v[index].l){
//		v[index].mini=mini(v[index].mini,v[v[index].l].mini);
		v[index].size+=v[v[index].l].size;
		v[index].maxi=max(v[index].maxi,v[v[index].l].maxi+v[index].add);
	}
	if(v[index].r){
//		v[index].mini=mini(v[index].mini,v[v[index].r].mini);
		v[index].size+=v[v[index].r].size;
		v[index].maxi=max(v[index].maxi,v[v[index].r].maxi+v[index].add);
	}
}
void push_down(int index){
	if(v[index].flag){
		//this must be reversed
		if(v[index].l){
			v[v[index].l].flag^=1;
			swap(v[v[index].l].l,v[v[index].l].r);	
		}
		if(v[index].r){
			v[v[index].r].flag^=1;
			swap(v[v[index].r].l,v[v[index].r].r);	
		}
		v[index].flag=0;
	}
	
	if(v[index].l){
		v[v[index].l].add+=v[index].add;
		v[v[index].l].maxi+=v[index].add;
		v[v[index].l].val+=v[index].add;
//		update(v[index].l);
	}
	if(v[index].r){
		v[v[index].r].add+=v[index].add;
		v[v[index].r].maxi+=v[index].add;
		v[v[index].r].val+=v[index].add;
	}
	v[index].add=0;
//	update(index);
}
int cnt=0;
int getnewnode(int val,int block){
	node tmp;
	tmp.maxi=val;
	tmp.val=val;
	tmp.add=tmp.flag=0;
	tmp.size=1;
	tmp.l=tmp.r=0;
	tmp.block=block;
//	tmp.mini=b,lock;
	tmp.fix=random(1234567890);
	cnt++;
	v[cnt]=tmp;
	return cnt;
}

void split(int base,int& x,int& y,int boundary){
	if(!base){
		x=y=0;
		return;
	}
	if(v[base].size==boundary){
		x=base;
		y=0;
		update(x);
	}
	if(!boundary){
		x=0;
		y=base;
		update(y);
	}
	push_down(base); 
	if(v[v[base].l].size>=boundary){
		y=base;
		v[y]=v[base];
		split(v[base].l,x,v[y].l,boundary);
		update(y);
	}
	else{
		x=base;
		v[x]=v[base];
		split(v[base].r,v[x].r,y,boundary-v[v[base].l].size-1);
		update(x);
	}
} 
void split2(int base,int& x,int& y,int boundary){//=boundary
	if(!base){
		x=y=0;
		return;
	}
	push_down(base); 
	if(v[base].block>=boundary){
		y=base;
//		v[y]=v[base];
		split2(v[base].l,x,v[y].l,boundary);
		update(y);
	}
	else{
		x=base;
//		v[x]=v[base];
		split2(v[base].r,v[x].r,y,boundary);
		update(x);
	}
} 
int merge(int x,int y){
	if((!x)||(!y)){
		if(x+y){
			update(x+y);
		}
		return x+y;
	} 
	if(v[x].fix>v[y].fix){
		push_down(x);	
		v[x].r=merge(v[x].r,y);
		update(x);
		return x;
	}
	else{
		push_down(y);
		v[y].l=merge(x,v[y].l);
		update(y);
		return y;
	}
}
int root=1;
map <mp,bool> M;
int main(){
	srand(19260817);
	fastio;
	int n,k,m;
	cin>>n>>k>>m;
	int cnt=0;
	rb(i,1,m){
		int x,y;
		cin>>x>>y;
		int val=y+abs(x-k);
//		cerr<<"#"<
		if(M[II(x,y)]){
			cnt--;	
			if(cnt==0){
				cnt=0;
				M[II(x,y)]=0;
				cout<<0<<endl;
				continue;
			}
			else{
				int L,R;
				split2(root,L,R,val);
				int MID;
				split(R,MID,R,1);
				v[L].add--;
				v[L].val--;
				v[L].maxi--;
				root=merge(L,R);
			}
		}
		else{
			cnt++;
			if(cnt==1){
				root=getnewnode(val,val);
			}
			else{
				int L,R;
				split2(root,L,R,val);
				if(L){
				v[L].add++;
				v[L].val++;
				v[L].maxi++;
				}
//				cerr<<"@"<
				int Add=0;
				if(R)
					Add+=v[R].size;
				int MID=getnewnode(Add+val,val);
				L=merge(L,MID);
				root=merge(L,R); 
			}
		}
		cout<<max(0,v[root].maxi-n)<<endl;
		M[II(x,y)]^=1;
		
	}
	return 0;
}