神经网络架构搜索——可微分搜索 (Noisy-DARTS)
神经网络架构搜索——可微分搜索 (Noisy-DARTS)
- 动机
- FairDARTS: Sigmoid函数替换Softmax函数
- NoisyDARTS:skip-connection注入噪声
- 方法实现
- 如何加噪声?
- 加入怎样的噪声?
- 实验结果
- 架构参数可视化
- CIFAR-10实验结果
- ImageNet实验结果
- 消融实验
- 有噪声 vs. 无噪声
- 无偏噪声 vs. 有偏噪声
- 高斯噪声 vs. 均匀噪声
- 加性噪声 vs. 乘法噪声
小米实验室 AutoML 团队的NAS工作,针对现有DARTS框架在搜索阶段训练过程中存在 skip-connection 富集现象,导致最终模型出现大幅度的性能损失的问题,提出了通过向 skip-connection 注入噪声的方法,来抵消由于不公平竞争而导致的富集和性能损失问题,并且在 CIFAR-10 和 ImageNet 上分别取得了 97.61%和77.9% 的 SOTA 结果。
- 论文链接:http://arxiv.org/abs/2005.03566
- 源码链接:https://github.com/xiaomi-automl/NoisyDARTS
动机
目前 NAS 方法已经存在非常多,其中谷歌提出的 DARTS 方法,即可微分结构搜(Differentiable Architecture Search),引起了广大研究从业人员的关注与研究。但是DARTS 的可复现性不高,主要原因包括:
- 搜索过程中存在 skip-connection 富集现象,导致最终模型出现大幅度的性能损失问题。
- softmax离散化存在很大gap,结构参数最佳的操作和其他算子之间的区分度并不明显,这样选择的操作很难达到最优。
FairDARTS: Sigmoid函数替换Softmax函数
Softmax操作使不同操作之间的关系变为竞争关系,由于 skip connection 和其他算子的加和操作形成残差结构,这就导致了 skip connection 比其他算子有很大的优势,这种优势在竞争环境下表现为不公平优势并持续放大,而其他有潜力的操作受到排挤,因此任意两个节点之间通常最终会以 skip connection 占据主导,导致最终搜索出的网络性能严重不足。
FairDARTS 通过 sigmoid 使每种操作有自己的权重,这样鼓励不同的操作之间相互合作,最终选择算子的时候选择大于某个阈值的一个或多个算子,在这种情形下,所有算子的结构权重都能够如实体现其对超网性能的贡献,而且残差结构也得以保留,因此最终生成的网络不会出现性能崩塌,从而避免了原生 DARTS 的 skip-connection 富集而导致的性能损失问题。
a = array([0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9])
b = sigmod(a)
c = softmax(a)
b = array([0.52497919, 0.549834 , 0.57444252, 0.59868766, 0.62245933, 0.64565631, 0.66818777, 0.68997448, 0.7109495 ])
c = array([0.07205446, 0.0796325 , 0.08800752, 0.09726335, 0.10749263, 0.11879773, 0.13129179, 0.14509987, 0.16036016])
NoisyDARTS:skip-connection注入噪声
NoisyDARTS 是在 FairDARTS 基础上的推论,既然 skip connection 存在不公平优势,那么采用通过向 skip-connection 注入噪声的方法,来抵消由于不公平竞争而导致的富集和性能损失问题,并且在 CIFAR-10 和 ImageNet 上分别取得了 97.61% 和77.9% 的 SOTA 结果。
方法实现
如何加噪声?
NoisyDARTS 选择仅在前向传递的 skip-connection 的输入中加入噪声。
L = g ( y ) , y = f ( α s k i p ) ⋅ ( x + x ~ ) \mathcal{L}=g(y), \quad y=f\left(\alpha^{s k i p}\right) \cdot(x+\tilde{x}) L=g(y),y=f(αskip)⋅(x+x~)
其中 g ( y ) g(y) g(y)是损失函数, f ( α s k i p ) f\left(\alpha^{s k i p}\right) f(αskip)是 DATRS 中的 softmax 函数, x ~ \tilde{x} x~是加注的噪声。在向前传递加入噪声的时候,后向对 α s k i p \alpha^{s k i p} αskip梯度更新的时候,就要将噪声一起计算在内:
∂ L ∂ α s k i p = ∂ L ∂ y ∂ y ∂ α s k i p = ∂ L ∂ y ∂ f ( α s k i p ) ∂ α s k i p ( x + x ~ ) \frac{\partial \mathcal{L}}{\partial \alpha^{s k i p}}=\frac{\partial \mathcal{L}}{\partial y} \frac{\partial y}{\partial \alpha^{s k i p}}=\frac{\partial \mathcal{L}}{\partial y} \frac{\partial f\left(\alpha^{s k i p}\right)}{\partial \alpha^{s k i p}}(x+\tilde{x}) ∂αskip∂L=∂y∂L∂αskip∂y=∂y∂L∂αskip∂f(αskip)(x+x~)
加入怎样的噪声?
加入噪声会为梯度更新带来不确定性,因此选择噪声的原则首先要保持梯度的更新是有效的。NoisyDARTS 提出,应该加注一种无偏的并且方差较小的噪声,比如本文实验中使用均值为0,方差很小的高斯分布作为噪声。因为噪声相对输入很小,所以可以做如下估计:
y ⋆ ≈ f ( α ) ⋅ x when x ~ ≪ x y^{\star} \approx f(\alpha) \cdot x \quad \text { when } \quad \tilde{x} \ll x y⋆≈f(α)⋅x when x~≪x
这样做的近似好处在于,我们可以近似认为梯度的期望也是无偏的:
E [ ∇ s k i p ] = E [ ∂ L ∂ y ∂ f ( α s k i p ) ∂ α s k i p ( x + x ~ ) ] ≈ ∂ L ∂ y ⋆ ∂ f ( α s k i p ) ∂ α s k i p ( x + E [ x ~ ] ) \mathbb{E}\left[\nabla_{s k i p}\right]=\mathbb{E}\left[\frac{\partial \mathcal{L}}{\partial y} \frac{\partial f\left(\alpha^{s k i p}\right)}{\partial \alpha^{s k i p}}(x+\tilde{x})\right] \approx \frac{\partial \mathcal{L}}{\partial y^{\star}} \frac{\partial f\left(\alpha^{s k i p}\right)}{\partial \alpha^{s k i p}}(x+\mathbb{E}[\tilde{x}]) E[∇skip]=E[∂y∂L∂αskip∂f(αskip)(x+x~)]≈∂y⋆∂L∂αskip∂f(αskip)(x+E[x~])
其中噪声是均值为0的高斯分布,所以 E [ x ~ ] = 0 E[\tilde{x}]=0 E[x~]=0。
class Identity(nn.Module):
def __init__(self):
super().__init__()
def forward(self, x):
return x + (0.1**0.5)*torch.randn_like(x) # add (0,0.1) Gaussian Noisy
实验结果
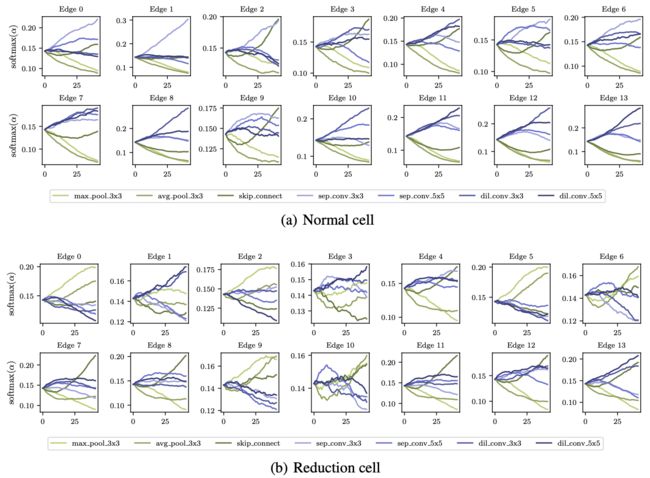
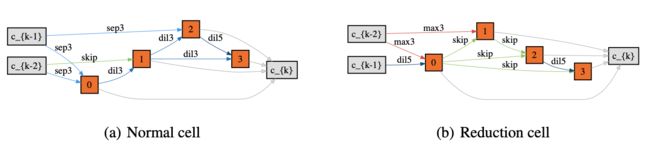
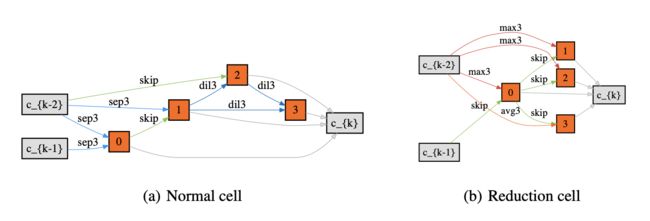
架构参数可视化
上图展示的是在 supernet 训练过程中,不同的操作在 softmax 下的权重变化,其中深绿色的线是 skip-connection 被 softmax 分配的权重。这张图中可以看到,normal cell中 的 skip-connection 数量被极大的消减了,同时保留了 reduction-cell 中的 skip-connection。
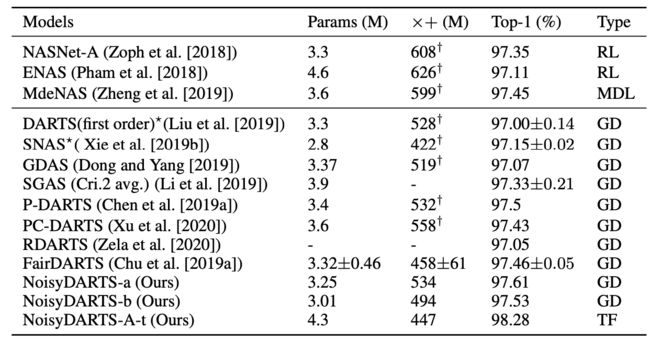
CIFAR-10实验结果
下图展示的是在 CIFAR-10 上,NoisyDARTS 与其他主流 NAS 方法相比的结果,其中 NoisyDARTS-A-t 是在 ImageNet上 训练得到的模型,迁移到 CIFAR-10 上训练得到的结果:
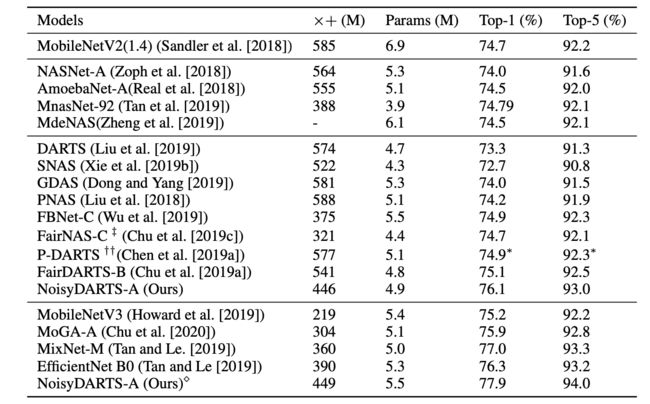
ImageNet实验结果
消融实验
有噪声 vs. 无噪声
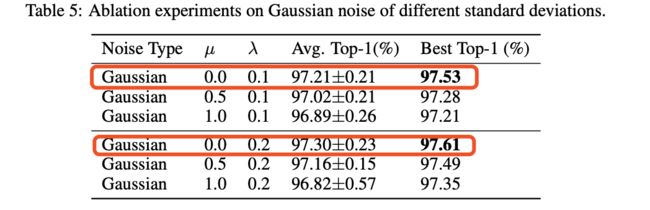
无偏噪声 vs. 有偏噪声
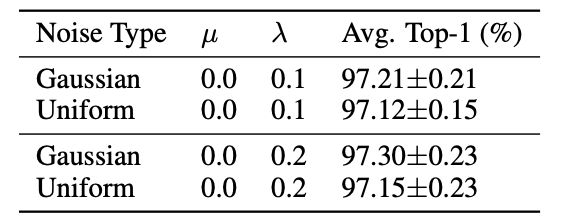
高斯噪声 vs. 均匀噪声
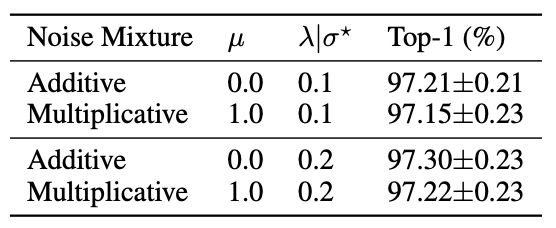
加性噪声 vs. 乘法噪声
![]()