神经网络架构搜索——可微分搜索（Fair-DARTS）

小米实验室 AutoML 团队的NAS工作，论文题目：Fair DARTS: Eliminating Unfair Advantages in Differentiable Architecture Search。 针对现有DARTS框架在搜索阶段训练过程中存在 skip-connection 富集现象，导致最终模型出现大幅度的性能损失问题的问题，提出了Sigmoid替代Softmax的方法，使搜索阶段候选操作由竞争关系转化为合作关系。 并提出 0-1 loss 提高了架构参数的二值性。

• 论文链接：https://arxiv.org/abs/1911.12126.pdf
• 源码链接：https://github.com/xiaomi-automl/FairDARTS

动机

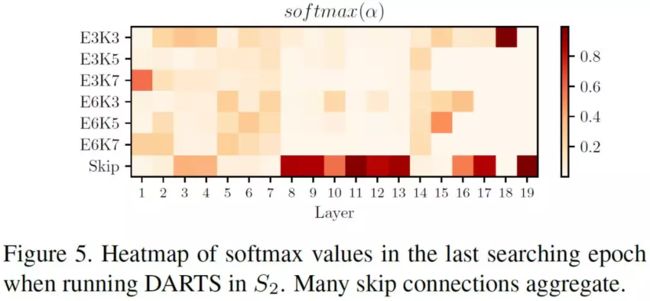
skip-connection 富集现象

本文指出 skip connections 富集的原因主要有两个方面：

skip connections 的不公平优势

在超网络训练架构参数过程中，两个节点之间是八个操作同时作用的， skip connections 作为操作的其中一员，相较于其他的操作来讲是起到了跳跃连接的作用。在ResNet 中已经明确指出了跳跃连接在深层网络的训练过程中中起到了良好的梯度疏通效果，进而有效减缓了梯度消失现象。因此，在超网络的搜索训练过程中，skip connections可以借助其他操作的关系达到疏通效果，使得，skip connections 相较于其他操作存在不公平优势。

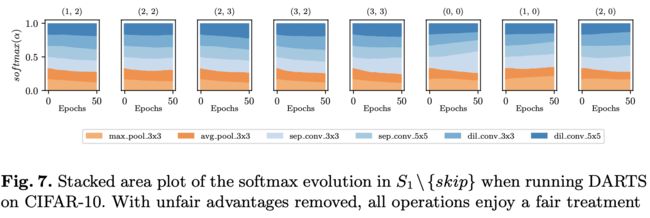
softmax 的排外竞争

由于 softmax 是典型的归一化操作，是一种潜在的排外竞争方式，致使一个架构参数增大必然抑制其他参数。

部署训练的离散化差异（discretization discrepancy）

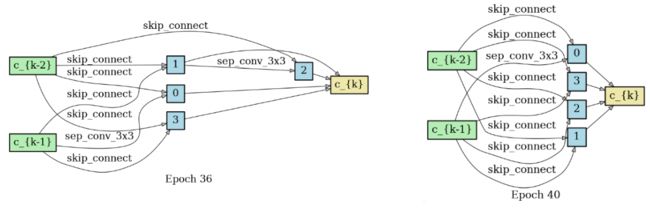
搜索过程结束后，在部署训练选取网络架构时，直接将 softmax 后最大 α 值对应的操作保留而抛弃其它的操作，从而使得选出的网络结构和原始包含所有结构的超网二者的表现能力存在差距。离散化差异问题主要在于两点，一方面Softmax归一化八种操作参数后，DARTS 最后选择时的 α 值基本都在 0.1 到 0.3 之间，另一方面判定好坏的范围比较窄，因为不同操作 α 值的 top1 和 top2 可能差距特别小，例如 0.26 和 0.24，很难说 0.26 就一定比 0.24 好，如下图所示：

方法

sigmoid 函数替换 softmax

class Network(nn.Module):

	def __init__(self, C, num_classes, layers, criterion, steps=4, multiplier=4, stem_multiplier=3,parse_method='darts', op_threshold=None):
		pass

	def forward(self, input):
		s0 = s1 = self.stem(input)
		for i, cell in enumerate(self.cells):
			if cell.reduction:
        		weights = F.sigmoid(self.alphas_reduce) # sigmoid 替换softmax
      		else:
        		weights = F.sigmoid(self.alphas_normal) # sigmoid 替换softmax
      		s0, s1 = s1, cell(s0, s1, weights)
    	out = self.global_pooling(s1)
    	logits = self.classifier(out.view(out.size(0),-1))
    	return logits

0-1 损失函数

l2 0-1 损失函数

$$L_{0-1}=-\frac{1}{N}\sum _i^N{\left(\sigma \left({\alpha }_i\right)-0.5\right)}^2$$

l1 0-1 损失函数

$$L_{0-1}^{\prime }=-\frac{1}{N}\sum _i^N\left|\left(\sigma \left({\alpha }_i\right)-0.5\right)\right|$$

$$L_{\text{total}}={\mathcal{L}}_{val}\left(w^{\ast }(\alpha ),\alpha \right)+w_{0-1}{L}_{0-1}$$

# l2
class ConvSeparateLoss(nn.modules.loss._Loss):
	"""Separate the weight value between each operations using L2"""
    def __init__(self, weight=0.1, size_average=None, ignore_index=-100,reduce=None, reduction='mean'):
        super(ConvSeparateLoss, self).__init__(size_average, reduce, reduction)
        self.ignore_index = ignore_index
        self.weight = weight

    def forward(self, input1, target1, input2):
        loss1 = F.cross_entropy(input1, target1)
        loss2 = -F.mse_loss(input2, torch.tensor(0.5, requires_grad=False).cuda())
        return loss1 + self.weight*loss2, loss1.item(), loss2.item()

# l1
class TriSeparateLoss(nn.modules.loss._Loss):
    """Separate the weight value between each operations using L1"""
    def __init__(self, weight=0.1, size_average=None, ignore_index=-100,
                 reduce=None, reduction='mean'):
        super(TriSeparateLoss, self).__init__(size_average, reduce, reduction)
        self.ignore_index = ignore_index
        self.weight = weight

    def forward(self, input1, target1, input2):
        loss1 = F.cross_entropy(input1, target1)
        loss2 = -F.l1_loss(input2, torch.tensor(0.5, requires_grad=False).cuda())
        return loss1 + self.weight*loss2, loss1.item(), loss2.item()

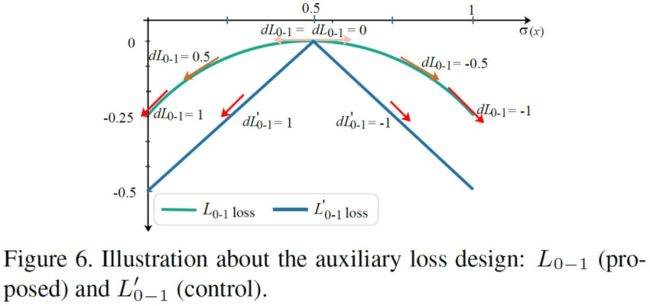
使用上述损失函数就可以使得不同操作之间的差距增大，二者的 α 值要么逼近 0 要么逼近 1 如下图曲线所示

实验

CIFAR-10

精度比较

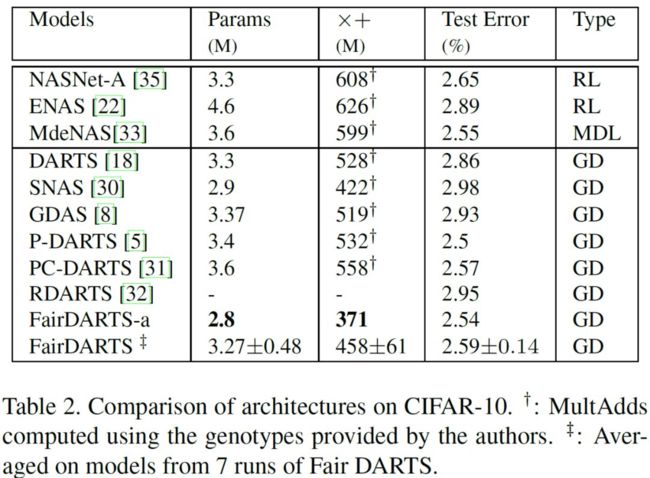
FairDARTS 搜索 7 次均可得到鲁棒性的结果:

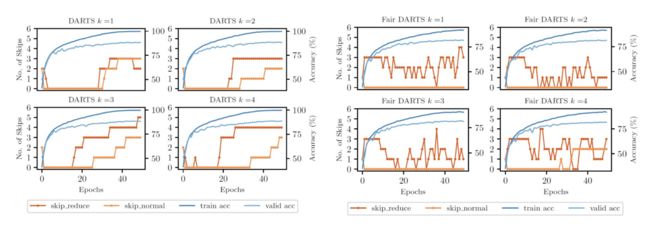
skip connections 数量比较

DARTS 和 Fair DARTS 搜索出来的 cell 中所包含的 skip connections 数量比较:

ImageNet

精度比较

注意模型 A、B 是迁移比较，C、D 是直接搜索比较。

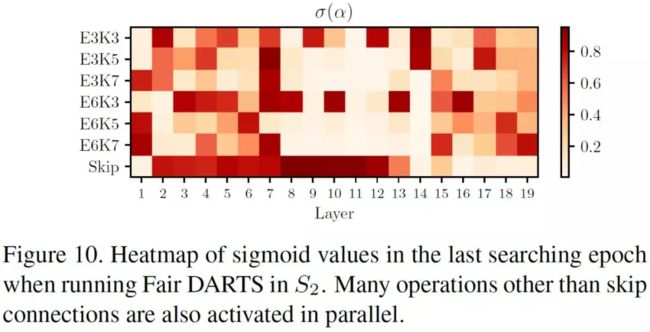
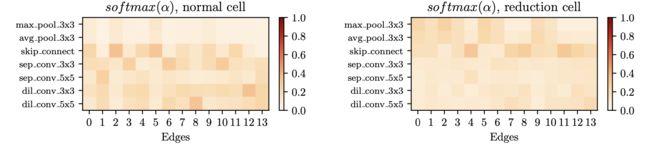
sigmoid 函数的共存性

热力图可看出使用 sigmoid 函数可让其他操作和 skip connections 共存：

消融实验

去掉 Skip Connections

由于不公平的优势主要来自 Skip Connections，因此，搜索空间去掉 Skip Connections，那么即使在排他性竞争中，其他操作也应该期待公平竞争。 去掉 Skip Connections搜索得到的最佳模型（96.88±0.18％）略高于DARTS（96.76±0.32％），但低于FairDARTS（97.41±0.14％）。 降低的精度表明足够的 Skip Connections 确实对精度有益，因此也不能简单去掉。

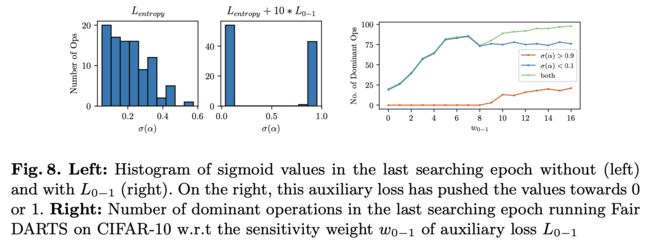
0-1 损失函数分析

• 如果去掉 0-1 损失函数会使得 α 值不再集中于两端，不利于离散化;
• 损失灵敏度，即通过超参来控制 $w_{0-1}$ 损失函数的灵敏度

讨论

• 对于 skip connections 使用 dropout 可以减少了不公平性；

• 对所有操作使用 dropout 同样是有帮助的；

• 早停机制同样关键（相当于是在不公平出现以前及时止损）；

• 限制 skip connections 的数量需要极大的人为先验，因为只要限定 skip connections 的数量为 2，随机搜索也能获得不错的结果；

• 高斯噪声或许也能打破不公平优势（孕育出了后面的NoisyDARTS~）。

参考

[1] Fair DARTS: Eliminating Unfair Advantages in Differentiable Architecture Search
[2] DARTS+: Improved Differentiable Architecture Search with Early Stopping
[3] Noisy Differentiable Architecture Search
[4] Fair DARTS：公平的可微分神经网络搜索
[5] Fair darts代码解析

---