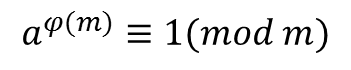Miller_Rabin素数测试[Fermat小定理][二次探测定理][同余式][Wilson定理]
部分引用自:
http://blog.csdn.net/fisher_jiang/article/details/986654
很大部分引用自:
http://www.matrix67.com/blog/archives/234
从零开始~
同余式
同余式的定义
如果两个正整数a和b之差能被n整除,我们就说a和b对模n同余,记作 a ≡ b (mod n)
同余式的运算
+ - * 均可, / 的时候注意:
-
若c与n互质,则有 a / c ≡ b / c ( mod n )简单解释: 如果ac≡bc(mod m),且c和m互质,则a≡b(mod m) (就是说同余式两边可以同时除以一个和模数互质的数)。
证明:条件告诉我们,ac-mp = bc-mq,移项可得ac-bc = mp-mq,也就是说(a-b)c = m(p-q)。这表明,(a-b)c里需要含有因子m,但c和m互质,因此只有可能是a-b被m整除,也即a≡b(mod m)。 [matrix67] -
若a / c ≡ b / c ( mod n ) , 则不一定有c与n互质.反例: 4 ≡ 64 (mod 10) 两边同除以c = 2 (n = 10)2 ≡ 32 (mod 10)
Wilson定理
当且仅当p为素数时:( p -1 )! ≡ -1 ( mod p ).
简要来说就是{ 2..p-2 }之间的数可以两两配对,乘积与1模p同余.
因此这些连乘的部分都可以换成1,只剩下了 1* ( p-1 ).由最后一式,得证.
[但是为什么可以两两配对, 目前还没看懂, 以后看懂了补上吧]
Wilson定理有很高的理论价值.但实际用于素数测试所需要计算量太大,无法实现对较大素数的测试.到目前为止,尚未找到素数测试的有效的确定性算法.
Fermat小定理
著名的费马小定理为素数判定提供了一个有力的工具.
费马小定理:如果p是一个素数,且(0
![]()
证明是容易的.
![]()
Euler定理
Euler对这个定理进行了推广,叫做Euler定理,有些地方叫做Fermat小定理的Euler推广。Euler定理中需要用一个函数f(m),它表示小于m的正整数中有多少个数和m互素(两个数只有公约数1称为互素)。为了方便,我们通常用记号φ(m)来表示这个函数(称作Euler函数)。
Euler指出,如果a和m互素,那么
可以看到,当m为素数时,φ(m)就等于m-1(所有小于m的正整数都与m互素),因此它是Fermat小定理的推广。定理的证明和Fermat小定理几乎相同,只是要考虑的式子变成了所有与m互素的数的乘积:
Fermat素数测试
1819年有人发现了Fermat小定理逆命题的第一个反例:虽然2的340次方除以341余1,但341=11*31。后来,人们又发现了561, 645, 1105等数都表明a=2时Fermat小定理的逆命题不成立。人们把所有能整除2^(n-1)-1的合数n叫做伪素数(pseudoprime)。
不满足![]() 的n一定不是素数;如果满足的话则多半是素数。这样,一个比试除法效率更高的素性判断方法出现了:制作一张伪素数表,记录某个范围内的所有伪素数,那么所有满足
的n一定不是素数;如果满足的话则多半是素数。这样,一个比试除法效率更高的素性判断方法出现了:制作一张伪素数表,记录某个范围内的所有伪素数,那么所有满足![]() 且不在伪素数表中的n就是素数。之所以这种方法更快,是因为我们可以使用二分法快速计算
且不在伪素数表中的n就是素数。之所以这种方法更快,是因为我们可以使用二分法快速计算![]() 的值(快速幂)。
的值(快速幂)。
然而不借助伪素数表的时候,算法出错的概率太高,需要改进.
我们刚才只考虑了a=2的情况。一个合数可能在a=2时通过了测试,但a=3时的计算结果却排除了素数的可能。于是,人们扩展了伪素数的定义,称满足a^(n-1) mod n = 1的合数n叫做以a为底的伪素数(pseudoprime to base a)。
随机选择若干个小于待测数的正整数作为底数a进行若干次测试,只要有一次没有通过测试就立即把这个数扔回合数的世界。这就是Fermat素性测试。
费马小定理毕竟只是素数判定的一个必要条件.满足费马小定理条件的整数n未必全是素数.有些合数也满足费马小定理的条件***.这些合数被称作Carmichael数,前3个Carmichael数是561,1105,1729. Carmichael数是非常少的.在1~100000000范围内的整数中,只有255个Carmichael数.
***费马小定理的前提是a和n互质。当n本身就是素数的时候如果a
利用下面的二次探测定理可以对上面的素数判定算法作进一步改进,以避免将Carmichael数当作素数.
Miller_Rabin素数测试算法
二次探测定理优化
Miller和Rabin两个人的工作让Fermat素性测试迈出了革命性的一步,建立了Miller-Rabin素性测试算法。新的测试基于下面的定理:
如果p是素数,x是小于p的正整数,且![]() ,那么要么x=1,要么x=p-1。
,那么要么x=1,要么x=p-1。
这是显然的,因为![]() 相当于p能整除
相当于p能整除![]() ,也即p能整除(x+1)(x-1)。
,也即p能整除(x+1)(x-1)。
由于p是素数,那么只可能是x-1能被p整除(此时x=1) 或 x+1能被p整除(此时x=p-1)。
我们下面来演示一下上面的定理如何应用在Fermat素性测试上。前面说过341可以通过以2为底的Fermat测试,因为2^340 mod 341=1。如果341真是素数的话,那么2^170mod 341只可能是1或340;当算得2^170 mod 341确实等于1时,我们可以继续查看2^85除以341的结果。我们发现,2^85 mod 341=32,这一结果摘掉了341头上的素数皇冠
这就是Miller-Rabin素性测试的方法。不断地提取指数n-1中的因子2,把n-1表示成![]() (其中d是一个奇数)。那么我们需要计算的东西就变成了
(其中d是一个奇数)。那么我们需要计算的东西就变成了![]() 除以n的余数。于是,
除以n的余数。于是,![]() 要么等于1,要么等于n-1。如果
要么等于1,要么等于n-1。如果![]() 等于1,定理继续适用于
等于1,定理继续适用于![]() ,这样不断开方开下去,直到对于某个i满足
,这样不断开方开下去,直到对于某个i满足![]() 或者最后指数中的2用完了得到的
或者最后指数中的2用完了得到的![]() 。这样,Fermat小定理加强为如下形式:
。这样,Fermat小定理加强为如下形式:
尽可能提取因子2,把n-1表示成![]() ,如果n是一个素数,那么或者
,如果n是一个素数,那么或者![]() ,或者存在某个i使得
,或者存在某个i使得![]() ( 0<=i
( 0<=i
Miller-Rabin素性测试同样是不确定算法,我们把可以通过以a为底的Miller-Rabin测试的合数称作以a为底的强伪素数(strong pseudoprime)。第一个以2为底的强伪素数为2047。第一个以2和3为底的强伪素数则大到1 373 653。
Miller-Rabin算法的代码也非常简单:计算d和r的值(可以用位运算加速,即快速积,快速幂),然后二分计算 的值,最后把它平方r次。
的值,最后把它平方r次。
/*对应hoj 1356 Prime Judge*/
#include
#define MT 5
using namespace std;
typedef long long ll;
int prime[] = {2, 3, 7, 61, 24251};
inline ll mulmod(ll a, ll b, ll k) {//*标出了核心语句
/* // a %= k;
// b %= k;
if (b < 0) {///将b变为正的
a = -a;
b = -b;
}
ll re = 0, temp = a;
///re为最终结果,temp保持循环.re需要temp的时候,就加一下,否则temp继续累乘
while (b) {
if (b & 1) re += temp;///二进制思想,需要即加*
// re %= k;
b >>= 1;///下一位等待检测**
temp <<= 1;///temp一直累乘***
// temp %= k;
}
return re%k;*/
/*实际上呢,用以上的函数在hoj 1356是会TLE的(mod太多次了...)~应该用下面的方法...*/
return (a*b)%k;//-_-b
}
//此时不需要再模,于是只剩下核心语句~快速幂和快速积都是二进制思想,核心是一样的
inline ll powermod(ll a, ll b, ll k) {
ll re = 1, temp = a;
while (b) {
if (b & 1) re = mulmod(re, temp, k);//只是把"加"入答案变为"乘"入答案
temp = mulmod(temp, temp, k);
b >>= 1;
}
return re;
}
int TwiceDetect(ll a, ll b, ll k) {
int t = 0;
ll x, y;
while ((b & 1) == 0) {
b >>= 1;
t++;
}
/// b = d * 2^t; b = d;
y = x = powermod(a, b, k);/// x = y = a^d % n
///二次探测定理是反向递归的,当然也可以用如下的正向迭代法去测试
while (t--) {
y = mulmod(x, x, k);
if (y == 1 && x != 1 && x != k - 1)///注意y!=1的时候是不做判断的,即对应
return 0;///递归时在某一环节x==p-1的情况,对此x开方则无意义,但是迭代的话不能break,只能ignore并继续.
x = y;///继续向高次迭代,那么至少最后一次应该是等于1的(Fermat小定理)
}
return y;
}
bool Miller_Rabin(ll n) {
int i;
ll tmp;
for (i = 0; i < MT; i++) {
tmp = prime[i];
if (n == prime[i]) return true;
if (TwiceDetect(tmp, n - 1, n) != 1)
break;
}
return (i == MT);
}
int main() {
ll n;
while (scanf("%lld", &n) == 1) {
if ((n > 1) && Miller_Rabin(n)) {
printf("YES\n");
} else {
printf("NO\n");
}
}
return 0;
}
对于大数的素性判断,目前Miller-Rabin算法应用最广泛。一般底数仍然是随机选取,但当待测数不太大时,选择测试底数就有一些技巧了。比如,如果被测数小于4 759 123 141,那么只需要测试三个底数2, 7和61就足够了。当然,你测试的越多,正确的范围肯定也越大。如果你每次都用前7个素数(2, 3, 5, 7, 11, 13和17)进行测试,所有不超过341 550 071 728 320的数都是正确的。如果选用2, 3, 7, 61和24251作为底数,那么10^16内唯一的强伪素数为46 856 248 255 981。这样的一些结论使得Miller-Rabin算法在OI中非常实用。通常认为,Miller-Rabin素性测试的正确率可以令人接受,随机选取k个底数进行测试算法的失误率大概为4^(-k)。
部分引用自:
http://blog.csdn.net/fisher_jiang/article/details/986654
很大部分引用自:
http://www.matrix67.com/blog/archives/234
![Miller_Rabin素数测试[Fermat小定理][二次探测定理][同余式][Wilson定理]_第1张图片](http://img.e-com-net.com/image/info8/431bf07e2e744255863e034dc51696bc.jpg)