球面坐标系

本文主要解决在球面上一点A,经纬度为($\theta ,\varphi$), 朝着与经线成$\psi$角转动，走了$\ell$长度之后的新坐标系(${\theta }^{\prime },{\varphi }^{\prime }$), 求新坐标系的值以及跟新经线的新夹角是多少。

（一）球面正弦定理余弦定理

在球面上画一个三角形，如下图$\Delta ABC$

∠A对应的边为$a$,(弧度单位)，假设球半径为$r$，则满足如下的余弦定理：

以及正弦定理：

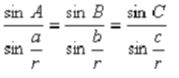
如果是单位球，即半径等于1，则正弦定理和余弦定理如下：

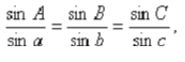
（二）新坐标的求解

如图，已经知道点$A(\theta ,\varphi )$, AB是经线，沿着与AB经线成一个角度$\psi$的方向AC线（不一定是经线）走动距离$\ell$到点C，求点C的经纬度(${\theta }^{\prime },{\varphi }^{\prime }$),以及BC经线与球面上的线AC的夹角$\alpha$.
求解过程如下：

两次利用余弦定理即可把夹角$\alpha$求出来
接下来要求经纬度(${\theta }^{\prime },{\varphi }^{\prime }$)，这里需要考虑到点A是东经还是西经，南纬还是北纬的问题，先在这里不考虑，接下来一节再讨论这个问题

程序实现如下

import numpy as np

def point_change(init_longi,init_lati,r,psi):
    psi = np.deg2rad(psi)
    ang_c = np.pi/2-np.deg2rad(init_lati) 
    cos_a = np.cos(r)*np.cos(ang_c)+np.sin(r)*np.sin(ang_c)*np.cos(psi)
    new_lati = np.abs(90-np.rad2deg(np.arccos(cos_a)))
    new_longi = np.abs(init_longi-np.rad2deg(np.arcsin(np.sin(psi)*np.sin(r)/np.sqrt(1-cos_a**2))))
    angle_change = np.rad2deg(np.arccos((np.cos(ang_c)-cos_a*np.cos(r))/(np.sqrt(1-cos_a**2)*np.sin(r))))
    angle_change = 180 - angle_change
    return angle_change, new_longi, new_lati

if __name__ == "__main__":    
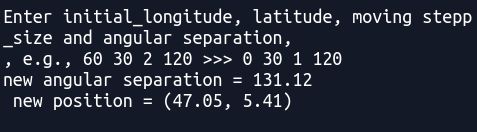
    init_longitude, init_latitude, move_step_size, init_included_angle = map(int,input('Enter initial_longitude, latitude, moving stepp\
                                                                               _size and angular separation,\n, e.g., 60 30 2 120 >>> ').split())
    
    # The unit of r is rad 
    #included_angle, new_longi, new_lati = point_change(60,30,2,120)
    included_angle, new_longi, new_lati = point_change(init_longitude, init_latitude, move_step_size, init_included_angle)
    print("new angular separation = %.2f \n new position = (%.2f, %.2f) \n" %(included_angle, new_longi, new_lati))

运行结果

（三）讨论点A东经西经南北纬问题

上面的程序是在没有考虑东西经度，南北纬度的情况。
东西经度的划分：面对一个地球仪经线0度，上方为北极，则左边是西经（经度往左逐渐增大），右边是东经（经度往右逐渐增大），下方是南纬，上方是北纬。
1）讨论经度
假设转动的角$\psi \le 180$, 表明移动后的点C是在点A的左边。

• 点A初始点在西经，则在求得∠B之后，需要用${\theta }^{\prime }=\theta +\angle B$得到的还是西经；然而需要注意的是如果$\theta +\angle B>180$, 则变成了东经，大小为abs$(\theta +\angle B-360)$,
• 点A初始点在东经， 则在求得∠B之后，需要用${\theta }^{\prime }=\theta -\angle B$得到的还是东经；然而需要注意的是如果$\theta -\angle B\le 0$, 则变成了西经，大小为abs$(\theta -\angle B)$

假设转动的角$\psi >180$, 表明移动后的点C是在点A的右边。

• 点A初始点在西经，则在求得∠B之后，需要用${\theta }^{\prime }=\theta -\angle B$得到的还是西经；然而需要注意的是如果$\theta -\angle B\le 0$, 则变成了东经，大小为abs$(\theta -\angle B)$,
• 点A初始点在东经， 则在求得∠B之后，需要用${\theta }^{\prime }=\theta +\angle B$得到的还是东经；然而需要注意的是如果$\theta +\angle B>180$, 则变成了西经，大小为abs$(\theta +\angle B-360)$

因此伪代码如下：

begin
    if psi <= 180：
        if theta is west longitude:
            if theta + B <=180:
                theta' = theta+B (west longitude)
            else:  theta' = abs(theta+B - 360) (east longitude)
        else:
            if theta - B > 0:
                 theta' = theta-B (east longitude)
            else:  theta' = abs(theta-B) (west longitude)
    elif psi > 180:
        if theta is east longitude:
            if theta + B <=180:
                theta' = theta+B (east longitude)
            else:  theta' = abs(theta+B - 360) (west longitude)
        else:
            if theta - B > 0:
                 theta' = theta-B (west longitude)
            else:  theta' = abs(theta-B) (east longitude)
end

由于往右边走，即$\psi >180$时， ∠B是负数，因此上面的两者可以结合起来，
无论夹角是否大于180度

• 点A初始点在西经，则在求得∠B之后，需要用${\theta }^{\prime }=\theta +\angle B$得到的还是西经；然而需要注意的是如果$\theta +\angle B>180$, 则变成了东经，大小为abs$(\theta +\angle B-360)$, 如果$\theta +\angle B<0$, 则值变为abs($\theta +\angle B$), 东经
• 点A初始点在东经， 则在求得∠B之后，需要用${\theta }^{\prime }=\theta -\angle B$得到的还是东经；然而需要注意的是如果$\theta -\angle B\le 0$, 则变成了西经，大小为abs$(\theta -\angle B)$，如果$\theta -\angle B<0$, 则值变为abs($\theta -\angle B$), 西经

2）讨论纬度
因为我们计算的点B是位于北极点(无论点A在南纬还是北纬)，所以以BC的边长a作为判断依据
如果A是北纬

• 如果$\pi /2-$a > 0, 则是北纬rad2deg($\pi /2-$a)度； #弧度化为度
• 如果$\pi /2-$a < 0, 则是南纬rad2deg（abs($\pi /2-$a))度；

如果A是南纬

• 如果$\pi /2-$a > 0, 则是北纬rad2deg($\pi /2-$a)度； #弧度化为度
• 如果$\pi /2-$a < 0, 则是南纬rad2deg（abs($\pi /2-$a))度；

因此对于南北纬都是一样的结论（因为是以a为判据，B在北极点）
伪代码：

if pi/2-a>0:
    theta' = np.rad2deg(pi/2-a) (North latitude)
else: theta' = np.rad2deg(abs(pi/2-a)) (south latitude)

由于三角函数本身的限制，比如图中49°和131°的sin值是一样的，都是0.75，即
$$\sin (49°)=\sin (131°)=0.75$$
当反推时arcsin(0.75)程序上只能给小值49.

因此在上面的过程中有以下要求：

• 在球面上移动的步长不能超过90度，即弧度值不能超过1.5

源码如下：

import numpy as np

def point_change(init_lon,w_e,init_lat,s_n,r,psi):
    psi = np.deg2rad(psi)
    ang_c = np.pi/2-np.deg2rad(init_lat) 
    cos_a = np.cos(r)*np.cos(ang_c)+np.sin(r)*np.sin(ang_c)*np.cos(psi)
    new_lati = np.abs(90-np.rad2deg(np.arccos(cos_a)))
    ang_B = np.rad2deg(np.arcsin(np.sin(psi)*np.sin(r)/np.sqrt(1-cos_a**2)))
    a_val = abs(np.arccos(cos_a))
    new_longi = np.abs(init_lon-np.rad2deg(np.arcsin(np.sin(psi)*np.sin(r)/np.sqrt(1-cos_a**2))))
    # East or west longitude
    if w_e is 'W':
        if (init_lon + ang_B) <= 180 and (init_lon + ang_B)>0:
            new_longi = init_lon + ang_B
            W_E = 'W'
        elif init_lon + ang_B > 180:
            new_longi = abs(init_lon + ang_B -360)
            W_E = 'E'
        elif init_lon + ang_B < 0:
            new_longi = abs(init_lon +ang_B)
            W_E = 'E'
    elif w_e is 'E':
        if (init_lon - ang_B) <= 180 and (init_lon - ang_B)>0:
            new_longi = init_lon - ang_B
            W_E = 'E'
        elif init_lon - ang_B > 180:
            new_longi = abs(init_lon - ang_B -360)
            W_E = 'E'
        elif init_lon - ang_B < 0:
            new_longi = abs(init_lon - ang_B)
            W_E = 'W'
    # South or north latitude
    if (np.pi/2 - a_val)>0:
        S_N = 'N'
    else: S_N = 'S'
    angle_change = np.rad2deg(np.arccos((np.cos(ang_c)-cos_a*np.cos(r))/(np.sqrt(1-cos_a**2)*np.sin(r))))
    angle_change = 180 - angle_change
    return angle_change, new_longi, W_E, new_lati, S_N

if __name__ == "__main__":   
    # The unit of r is rad 
    # The moving step_size should be less than 90*pi/180
    
#    # input from terminal
#    init_longitude, w_e_input, init_latitude, s_n_input, move_step_size, init_included_angle = \
#    map(str,input('Enter initial_longitude, latitude, moving step_size and angular separation,\n, e.g., 60 E 30 N 1 120 >>> ').split())
#    init_longitude = float(init_longitude)
#    init_latitude = float(init_latitude)
#    move_step_size = float(move_step_size)
#    init_included_angle = float(init_included_angle)
#    included_angle, new_longi, w_e, new_lati, s_n = \
#    point_change(init_longitude, w_e_input, init_latitude, s_n_input, move_step_size, init_included_angle)
    
    #input from code
    included_angle, new_longi, w_e, new_lati, s_n = point_change(0,'W',0,'N',60*np.pi/180,90)
    print(('new angular separation = %.2f\n new position = (%.2f'+w_e+', %.2f'+s_n+')')%(included_angle, new_longi, new_lati))

比如：原来的位置为西经30度北纬60度，沿着与经线成120度方向（此程序中是逆时针方向）后，得到的与新经线的夹角为153.38度，新坐标为经度78.95度，纬度14.92度