【运筹学】线性规划 人工变量法 阶段总结 ( 使用 人工变量法 求解 线性规划 全过程详细解析 ) ★
文章目录
- 一、人工变量法案例
- 二、线性规划标准型
- 三、添加人工变量
- 四、初始单纯形表
- 五、初始单纯形表 : 计算非基变量检验数
- 六、初始单纯形表 : 最优解判定
- 七、初始单纯形表 : 选择入基变量
- 八、初始单纯形表 : 选择出基变量
- 九、初始单纯形表 : 更新单纯形表
- 十、第一次迭代 : 中心元变换
- 十一、第一次迭代 : 单纯形表
- 十二、第一次迭代 : 计算检验数
- 十三、第一次迭代 : 最优解判定
- 十四、第一次迭代 : 选择入基变量
- 十五、第一次迭代 : 选择出基变量
- 十六、第一次迭代 : 更新单纯形表
- 十七、第二次迭代 : 中心元变换
- 十八、第二次迭代 : 单纯形表
- 十九、第二次迭代 : 计算检验数
- 二十、第二次迭代 : 最优解判定
- 二十一、第二次迭代 : 选择入基变量
- 二十二、第二次迭代 : 选择出基变量
- 二十三、第二次迭代 : 更新单纯形表
- 二十四、第三次迭代 : 中心元变换
- 二十五、第三次迭代 : 单纯形表
- 二十六、第三次迭代 : 检验数计算
- 二十七、第三次迭代 : 最优解判定
- 二十八、第三次迭代 : 最终单纯形表
一、人工变量法案例
求解线性规划 : 使用人工变量法求解线性规划 ;
m a x Z = 3 x 1 + 2 x 2 − x 3 s . t { − 4 x 1 + 3 x 2 + x 3 ≥ 4 x 1 − x 2 + 2 x 3 ≤ 10 − 2 x 1 + 2 x 2 − x 3 = − 1 x j ≥ 0 ( j = 1 , 2 , 3 ) \begin{array}{lcl} max Z = 3x_1 + 2x_2 - x_3 \\ \\ s.t\begin{cases} -4 x_1 + 3x_2 + x_3 \geq 4 \\\\ x_1 - x_2 + 2x_3 \leq 10 \\\\ -2x_1 + 2x_2 - x_3 = -1 \\\\ x_j \geq 0 & (j = 1 , 2 , 3 ) \end{cases}\end{array} maxZ=3x1+2x2−x3s.t⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧−4x1+3x2+x3≥4x1−x2+2x3≤10−2x1+2x2−x3=−1xj≥0(j=1,2,3)
二、线性规划标准型
参考 【运筹学】线性规划数学模型标准形式 ( 标准形式 | 目标函数转化 | 决策变量转化 | 约束方程转化 | 固定转化顺序 | 标准形式转化实例 ) 线性规划 普通形式 -> 标准形式 转化顺序说明 博客 , 先处理变量约束 , 再将不等式转为等式 , 最后更新目标函数 ;
1 . 处理约束变量 : 所有的约束变量都大于等于 0 0 0 , 这里无需处理 ;
2 . 将不等式转为等式 :
① 方程 1 1 1 转为等式 : 方程 1 1 1 是大于等于不等式 , 需要在方程左侧减去剩余变量 x 4 x_4 x4 ;
− 4 x 1 + 3 x 2 + x 3 − x 4 = 4 -4 x_1 + 3x_2 + x_3 - x_4 = 4 −4x1+3x2+x3−x4=4
② 方程 2 2 2 转为等式 : 方程 2 2 2 是小于等于不等式 , 需要在方程左侧加上松弛变量 x 5 x_5 x5 ;
x 1 − x 2 + 2 x 3 + x 5 = 10 x_1 - x_2 + 2x_3 + x_5 = 10 x1−x2+2x3+x5=10
3 . 方程 3 3 3 转为符合要求的等式 : 方程 3 3 3 是等式 , 但是其右侧的常数小于 0 0 0 , 这里需要在等式两边都乘以 − 1 -1 −1 , 使右侧的常数大于等于 0 0 0 ;
2 x 1 − 2 x 2 + x 3 = 1 2x_1 - 2x_2 + x_3 = 1 2x1−2x2+x3=1
4 . 处理目标函数取最大值 : 目标函数就是取最大值 , 无需处理 ;
5 . 最终的标准形结果是 :
m a x Z = 3 x 1 + 2 x 2 − x 3 s . t { − 4 x 1 + 3 x 2 + x 3 − x 4 = 4 x 1 − x 2 + 2 x 3 + x 5 = 10 2 x 1 − 2 x 2 + x 3 = 1 x j ≥ 0 ( j = 1 , 2 , 3 , 4 , 5 ) \begin{array}{lcl} max Z = 3x_1 + 2x_2 - x_3 \\ \\ s.t\begin{cases} -4 x_1 + 3x_2 + x_3 - x_4 = 4 \\\\ x_1 - x_2 + 2x_3 + x_5 = 10 \\\\ 2x_1 - 2x_2 + x_3 = 1 \\\\ x_j \geq 0 \quad (j = 1 , 2 , 3, 4, 5 ) \end{cases}\end{array} maxZ=3x1+2x2−x3s.t⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧−4x1+3x2+x3−x4=4x1−x2+2x3+x5=102x1−2x2+x3=1xj≥0(j=1,2,3,4,5)
三、添加人工变量
将上述转化完毕的标准型的系数矩阵补全 :
m a x Z = 3 x 1 + 2 x 2 − x 3 + 0 x 4 + 0 x 5 s . t { − 4 x 1 + 3 x 2 + x 3 − x 4 + 0 x 5 = 4 x 1 − x 2 + 2 x 3 + 0 x 4 + x 5 = 10 2 x 1 − 2 x 2 + x 3 + 0 x 4 + 0 x 5 = 1 x j ≥ 0 ( j = 1 , 2 , 3 , 4 , 5 ) \begin{array}{lcl} max Z = 3x_1 + 2x_2 - x_3 + 0x_4 + 0x_5 \\ \\ s.t\begin{cases} -4 x_1 + 3x_2 + x_3 - x_4 + 0x_5 = 4 \\\\ x_1 - x_2 + 2x_3 + 0x_4 + x_5 = 10 \\\\ 2x_1 - 2x_2 + x_3 + 0x_4 + 0x_5 = 1 \\\\ x_j \geq 0 \quad (j = 1 , 2 , 3, 4, 5 ) \end{cases}\end{array} maxZ=3x1+2x2−x3+0x4+0x5s.t⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧−4x1+3x2+x3−x4+0x5=4x1−x2+2x3+0x4+x5=102x1−2x2+x3+0x4+0x5=1xj≥0(j=1,2,3,4,5)
上述约束方程中没有单位阵 , 无法找到初始基可行解 , 创建初始的单纯形表 ;
上述线性规划中 , 需要找到 3 × 3 3 \times 3 3×3 的单位阵 ( 1 0 0 0 1 0 0 0 1 ) \begin{pmatrix} \quad 1 \quad 0 \quad 0 \quad \\ \quad 0 \quad 1 \quad 0 \quad \\ \quad 0 \quad 0 \quad 1 \quad \\ \end{pmatrix} ⎝⎛100010001⎠⎞ , 目前只有 x 5 x_5 x5 的系数列向量是 ( 0 1 0 ) \begin{pmatrix} \quad 0 \quad \\ \quad 1 \quad \\ \quad 0 \quad \\ \end{pmatrix} ⎝⎛010⎠⎞ , 这里需要进行如下操作 ;
人工变量法 : 目的是人为制造单位阵 , 添加 2 2 2 个或 3 3 3 个人工变量 ;
- 方程 1 1 1 构造变量 x 6 x_6 x6 : 该变量只出现在第 1 1 1 个方程中 ;
− 4 x 1 + 3 x 2 + x 3 − x 4 + 0 x 5 + x 6 = 4 -4 x_1 + 3x_2 + x_3 - x_4 + 0x_5 + x_6 = 4 −4x1+3x2+x3−x4+0x5+x6=4
- 方程 2 2 2 构造变量 x 7 x7 x7 : 该变量只出现在第 3 3 3 个方程中 ;
2 x 1 − 2 x 2 + x 3 + 0 x 4 + 0 x 5 + x 7 = 1 2x_1 - 2x_2 + x_3 + 0x_4 + 0x_5 + x_7 = 1 2x1−2x2+x3+0x4+0x5+x7=1
添加了人工变量后 , 变量就变成了 7 7 7 个 ( x 1 x 2 x 3 x 4 x 5 x 6 x 7 ) \begin{pmatrix} \quad x_1 \quad \\ \quad x_2 \quad \\ \quad x_3 \quad \\ \quad x_4 \quad \\ \quad x_5 \quad \\ \quad x_6 \quad \\ \quad x_7 \quad \\ \end{pmatrix} ⎝⎜⎜⎜⎜⎜⎜⎜⎜⎛x1x2x3x4x5x6x7⎠⎟⎟⎟⎟⎟⎟⎟⎟⎞ , 原来的变量只有 5 5 5 个 ( x 1 x 2 x 3 x 4 x 5 ) \begin{pmatrix} \quad x_1 \quad \\ \quad x_2 \quad \\ \quad x_3 \quad \\ \quad x_4 \quad \\ \quad x_5 \quad \\ \end{pmatrix} ⎝⎜⎜⎜⎜⎛x1x2x3x4x5⎠⎟⎟⎟⎟⎞ ; 如果解出该线性规划的 7 7 7 个解 , 去掉后面的 x 6 , x 7 x_6 , x_7 x6,x7 之后 , 该最优解不一定满足 5 5 5 个变量的线性规划 ;
如果解出的 7 7 7 个解中 , x 6 , x 7 x_6 , x_7 x6,x7 都等于 0 0 0 , 此时该最优解的前 5 5 5 个变量 , 满足最初的线性规划解 ;
引入大 M M M : 在目标函数中 , 为 x 6 , x 7 x_6 , x_7 x6,x7 加上系数 − M -M −M , M M M 是一个抽象数值 , 没有具体的值 , 其大于给定的任何一个值 ;
m a x Z = 3 x 1 + 2 x 2 − x 3 + 0 x 4 + 0 x 5 − M x 6 − M x 7 max Z = 3x_1 + 2x_2 - x_3 + 0x_4 + 0x_5 - M x_6 - Mx_7 maxZ=3x1+2x2−x3+0x4+0x5−Mx6−Mx7
引入大 M M M 后最优解 x 6 , x 7 x_6 , x_7 x6,x7 必须为 0 0 0 : 如果上述 x 6 , x 7 x_6 , x_7 x6,x7 只要大于 0 0 0 , 即使很小 , 但是乘以一个很大的负数值 − M -M −M , 也会极大降低目标函数大小 , 因此只有两个变量取值为 0 0 0 时 , 才能使该解称为最优解 ;
添加 2 2 2 个人工变量后 , 得到 人工变量单纯形法 线性规划模型 :
m a x Z = 3 x 1 + 2 x 2 − x 3 + 0 x 4 + 0 x 5 − M x 6 − M x 7 s . t { − 4 x 1 + 3 x 2 + x 3 − x 4 + 0 x 5 + x 6 + 0 x 7 = 4 x 1 − x 2 + 2 x 3 + 0 x 4 + x 5 + 0 x 6 + 0 x 7 = 10 2 x 1 − 2 x 2 + x 3 + 0 x 4 + 0 x 5 + 0 x 6 + x 7 = 1 x j ≥ 0 ( j = 1 , 2 , 3 , 4 , 5 , 6 , 7 ) \begin{array}{lcl} max Z = 3x_1 + 2x_2 - x_3 + 0x_4 + 0x_5 - M x_6 - Mx_7 \\\\ s.t\begin{cases} -4 x_1 + 3x_2 + x_3 - x_4 + 0x_5 + x_6 + 0x_7 = 4 \\\\ x_1 - x_2 + 2x_3 + 0x_4 + x_5 + 0x_6 + 0x_7 = 10 \\\\ 2x_1 - 2x_2 + x_3 + 0x_4 + 0x_5 + 0x_6 + x_7 = 1 \\\\ x_j \geq 0 \quad (j = 1 , 2 , 3, 4, 5 , 6 , 7 ) \end{cases}\end{array} maxZ=3x1+2x2−x3+0x4+0x5−Mx6−Mx7s.t⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧−4x1+3x2+x3−x4+0x5+x6+0x7=4x1−x2+2x3+0x4+x5+0x6+0x7=102x1−2x2+x3+0x4+0x5+0x6+x7=1xj≥0(j=1,2,3,4,5,6,7)
其中的 M M M 是一个很大的数值 , 没有具体的值 , 可以理解为正无穷 + ∞ +\infty +∞ , 具体使用单纯形法进行计算时 , 将其理解为大于给出的任意一个确定的数值 ;
四、初始单纯形表
添加 2 2 2 个人工变量后 , 得到 人工变量单纯形法 线性规划模型 :
m a x Z = 3 x 1 + 2 x 2 − x 3 + 0 x 4 + 0 x 5 − M x 6 − M x 7 s . t { − 4 x 1 + 3 x 2 + x 3 − x 4 + 0 x 5 + x 6 + 0 x 7 = 4 x 1 − x 2 + 2 x 3 + 0 x 4 + x 5 + 0 x 6 + 0 x 7 = 10 2 x 1 − 2 x 2 + x 3 + 0 x 4 + 0 x 5 + 0 x 6 + x 7 = 1 x j ≥ 0 ( j = 1 , 2 , 3 , 4 , 5 , 6 , 7 ) \begin{array}{lcl} max Z = 3x_1 + 2x_2 - x_3 + 0x_4 + 0x_5 - M x_6 - Mx_7 \\\\ s.t\begin{cases} -4 x_1 + 3x_2 + x_3 - x_4 + 0x_5 + x_6 + 0x_7 = 4 \\\\ x_1 - x_2 + 2x_3 + 0x_4 + x_5 + 0x_6 + 0x_7 = 10 \\\\ 2x_1 - 2x_2 + x_3 + 0x_4 + 0x_5 + 0x_6 + x_7 = 1 \\\\ x_j \geq 0 \quad (j = 1 , 2 , 3, 4, 5 , 6 , 7 ) \end{cases}\end{array} maxZ=3x1+2x2−x3+0x4+0x5−Mx6−Mx7s.t⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧−4x1+3x2+x3−x4+0x5+x6+0x7=4x1−x2+2x3+0x4+x5+0x6+0x7=102x1−2x2+x3+0x4+0x5+0x6+x7=1xj≥0(j=1,2,3,4,5,6,7)
其中的 M M M 是一个很大的数值 , 没有具体的值 , 可以理解为正无穷 + ∞ +\infty +∞ , 具体使用单纯形法进行计算时 , 将其理解为大于给出的任意一个确定的数值 ;
生成初始基可行表 :
| c j c_j cj | c j c_j cj | 3 3 3 | 2 2 2 | − 1 -1 −1 | 0 0 0 | 0 0 0 | − M -M −M | − M -M −M | ||
|---|---|---|---|---|---|---|---|---|---|---|
| C B C_B CB 基变量系数 (目标函数) | X B X_B XB 基变量 | 常数 b b b | x 1 x_1 x1 | x 2 x_2 x2 | x 3 x_3 x3 | x 4 x_4 x4 | x 5 x_5 x5 | x 6 x_6 x6 | x 7 x_7 x7 | θ i \theta_i θi |
| − M -M −M ( 目标函数 x 6 x_6 x6 系数 c 6 c_6 c6 ) | x 6 x_6 x6 | 4 4 4 | − 4 -4 −4 | 3 3 3 | 1 1 1 | − 1 -1 −1 | 0 0 0 | 1 1 1 | 0 0 0 | ? ? ? ( θ 6 \theta_6 θ6) |
| 0 0 0 ( 目标函数 x 5 x_5 x5 系数 c 5 c_5 c5) | x 5 x_5 x5 | 10 10 10 | 1 1 1 | − 1 -1 −1 | 2 2 2 | 0 0 0 | 1 1 1 | 0 0 0 | 0 0 0 | ? ? ? ( θ 5 \theta_5 θ5 ) |
| − M -M −M ( 目标函数 x 7 x_7 x7 系数 c 7 c_7 c7) | x 7 x_7 x7 | 1 1 1 | 2 2 2 | − 2 -2 −2 | 1 1 1 | 0 0 0 | 0 0 0 | 0 0 0 | 1 1 1 | ? ? ? ( θ 7 \theta_7 θ7 ) |
| σ j \sigma_j σj ( 检验数 ) | ? ? ? ( σ 1 \sigma_1 σ1 ) | ? ? ? ( σ 2 \sigma_2 σ2 ) | ? ? ? ( σ 3 \sigma_3 σ3 ) | ? ? ? ( σ 3 \sigma_3 σ3 ) | 0 0 0 | 0 0 0 | 0 0 0 |
注意基变量顺序 : 初始基可行解的单位阵的顺序 , 是 ( 1 0 0 0 1 0 0 0 1 ) \begin{pmatrix} \quad 1 \quad 0 \quad 0 \quad \\ \quad 0 \quad 1 \quad 0 \quad \\ \quad 0 \quad 0 \quad 1 \quad \\ \end{pmatrix} ⎝⎛100010001⎠⎞ , 对应的基变量顺序是 ( x 6 x 5 x 7 ) \begin{pmatrix} \quad x_6 \quad x_5 \quad x_7 \quad \\ \end{pmatrix} (x6x5x7)
-
x 6 x_6 x6 系数是 ( 1 0 0 ) \begin{pmatrix} \quad 1 \quad \\ \quad 0 \quad \\ \quad 0 \quad \\ \end{pmatrix} ⎝⎛100⎠⎞
-
x 5 x_5 x5 系数是 ( 0 1 0 ) \begin{pmatrix} \quad 0 \quad \\ \quad 1 \quad \\ \quad 0 \quad \\ \end{pmatrix} ⎝⎛010⎠⎞
-
x 7 x_7 x7 系数是 ( 0 0 1 ) \begin{pmatrix} \quad 0 \quad \\ \quad 0 \quad \\ \quad 1 \quad \\ \end{pmatrix} ⎝⎛001⎠⎞
五、初始单纯形表 : 计算非基变量检验数
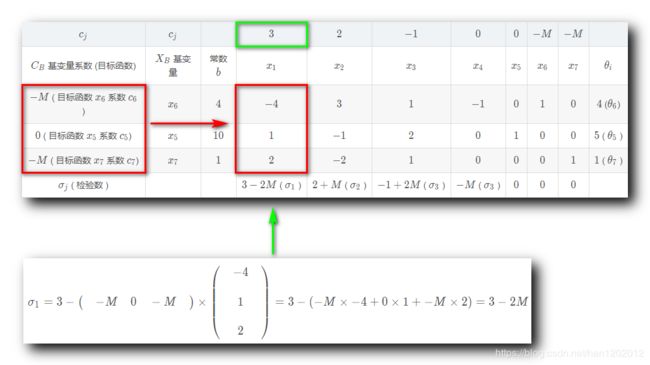
1 . 计算非基变量 x 1 x_1 x1 的检验数 σ 1 \sigma_1 σ1 :
σ 1 = 3 − ( − M 0 − M ) × ( − 4 1 2 ) = 3 − ( − M × − 4 + 0 × 1 + − M × 2 ) = 3 − 2 M \sigma_1 = 3 - \begin{pmatrix} \quad -M \quad 0 \quad -M \quad \\ \end{pmatrix} \times \begin{pmatrix} \quad -4 \quad \\\\ \quad 1 \quad \\\\ \quad 2 \quad \end{pmatrix} = 3- ( -M \times -4 + 0 \times 1 + -M \times 2) =3 - 2M σ1=3−(−M0−M)×⎝⎜⎜⎜⎜⎛−412⎠⎟⎟⎟⎟⎞=3−(−M×−4+0×1+−M×2)=3−2M
其中 M M M 是正无穷 + ∞ +\infin +∞ , 3 − 2 M 3 - 2M 3−2M 是负数 ;
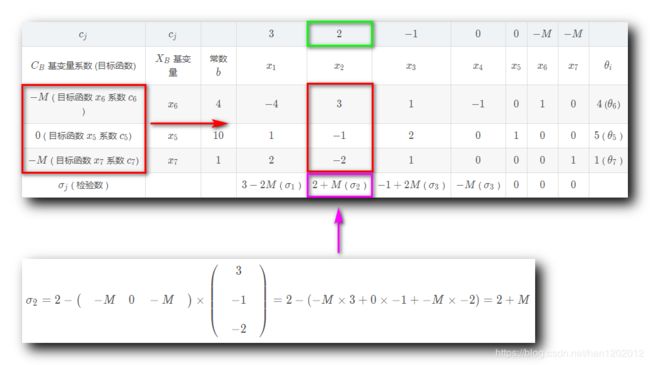
2 . 计算非基变量 x 2 x_2 x2 的检验数 σ 2 \sigma_2 σ2 :
σ 2 = 2 − ( − M 0 − M ) × ( 3 − 1 − 2 ) = 2 − ( − M × 3 + 0 × − 1 + − M × − 2 ) = 2 + M \sigma_2 = 2 - \begin{pmatrix} \quad -M \quad 0 \quad -M \quad \\ \end{pmatrix} \times \begin{pmatrix} \quad 3 \quad \\\\ \quad -1 \quad \\\\ \quad -2 \quad \end{pmatrix} = 2- ( -M \times 3 + 0 \times -1 + -M \times -2) = 2 + M σ2=2−(−M0−M)×⎝⎜⎜⎜⎜⎛3−1−2⎠⎟⎟⎟⎟⎞=2−(−M×3+0×−1+−M×−2)=2+M
其中 M M M 是正无穷 + ∞ +\infin +∞ , 2 + M 2 + M 2+M 是正数 ;
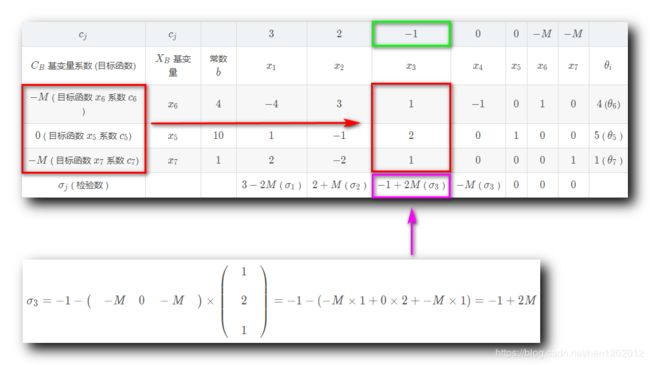
3 . 计算非基变量 x 3 x_3 x3 的检验数 σ 3 \sigma_3 σ3 :
σ 3 = − 1 − ( − M 0 − M ) × ( 1 2 1 ) = − 1 − ( − M × 1 + 0 × 2 + − M × 1 ) = − 1 + 2 M \sigma_3 = -1 - \begin{pmatrix} \quad -M \quad 0 \quad -M \quad \\ \end{pmatrix} \times \begin{pmatrix} \quad 1 \quad \\\\ \quad 2 \quad \\\\ \quad 1 \quad \end{pmatrix} = -1- ( -M \times 1 + 0 \times 2 + -M \times 1) =-1 + 2M σ3=−1−(−M0−M)×⎝⎜⎜⎜⎜⎛121⎠⎟⎟⎟⎟⎞=−1−(−M×1+0×2+−M×1)=−1+2M
其中 M M M 是正无穷 + ∞ +\infin +∞ , − 1 + 2 M -1 + 2M −1+2M 是正数 ;
4 . 计算非基变量 x 4 x_4 x4 的检验数 σ 4 \sigma_4 σ4 :
σ 4 = 0 − ( − M 0 − M ) × ( − 1 0 0 ) = 0 − ( − M × − 1 + 0 × 0 + − M × 0 ) = − M \sigma_4 = 0 - \begin{pmatrix} \quad -M \quad 0 \quad -M \quad \\ \end{pmatrix} \times \begin{pmatrix} \quad -1 \quad \\\\ \quad 0 \quad \\\\ \quad 0 \quad \end{pmatrix} = 0- ( -M \times -1 + 0 \times 0 + -M \times 0) =-M σ4=0−(−M0−M)×⎝⎜⎜⎜⎜⎛−100⎠⎟⎟⎟⎟⎞=0−(−M×−1+0×0+−M×0)=−M
其中 M M M 是正无穷 + ∞ +\infin +∞ , − M -M −M 是负数 ;
六、初始单纯形表 : 最优解判定
根据上述四个检验数 { σ 1 = 3 − 2 M ( 负 数 ) σ 2 = 2 + M ( 正 数 ) σ 3 = − 1 + 2 M ( 正 数 ) σ 4 = − M ( 负 数 ) \begin{cases} \sigma_1 = 3 - 2M \quad ( 负数 )\\\\ \sigma_2= 2 + M \quad ( 正数 )\\\\ \sigma_3= -1 + 2M \quad ( 正数 ) \\\\ \sigma_4 = -M \quad ( 负数 ) \end{cases} ⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧σ1=3−2M(负数)σ2=2+M(正数)σ3=−1+2M(正数)σ4=−M(负数) 的值 , 其中 σ 2 , σ 3 \sigma_2 , \sigma_3 σ2,σ3 检验数大于 0 0 0 , 该基可行解不是最优解 ;
只有当检验数都小于等于 0 0 0 时 , 该基可行解才是最优解 ;
七、初始单纯形表 : 选择入基变量
根据上述四个检验数 { σ 1 = 3 − 2 M σ 2 = 2 + M σ 3 = − 1 + 2 M σ 4 = − M \begin{cases} \sigma_1 = 3 - 2M\\\\ \sigma_2= 2 + M\\\\ \sigma_3= -1 + 2M \\\\ \sigma_4 = -M \end{cases} ⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧σ1=3−2Mσ2=2+Mσ3=−1+2Mσ4=−M 的值 , 选择检验数最大的非基变量作为入基变量 , σ 3 = − 1 + 2 M \sigma_3= -1 + 2M σ3=−1+2M 最大 , 这里选择 x 3 x_3 x3 ;
八、初始单纯形表 : 选择出基变量
出基变量选择 : 常数列 b = ( 4 10 1 ) b =\begin{pmatrix} \quad 4 \quad \\ \quad 10 \quad \\ \quad 1 \quad \\ \end{pmatrix} b=⎝⎛4101⎠⎞ , 分别除以除以入基变量 x 3 x_3 x3 大于 0 0 0 的系数列 ( 1 2 1 ) \begin{pmatrix} \quad 1 \quad \\\\ \quad 2 \quad \\\\ \quad 1 \quad \end{pmatrix} ⎝⎜⎜⎜⎜⎛121⎠⎟⎟⎟⎟⎞ , 计算过程如下 ( 4 1 10 2 1 1 ) \begin{pmatrix} \quad \cfrac{4}{1} \quad \\\\ \quad \cfrac{10}{2} \quad \\\\ \quad \cfrac{1}{ 1} \quad \end{pmatrix} ⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜⎛1421011⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟⎞ , 得出结果是 ( 4 5 1 ) \begin{pmatrix} \quad 4 \quad \\\\ \quad 5 \quad \\\\ \quad 1 \quad \end{pmatrix} ⎝⎜⎜⎜⎜⎛451⎠⎟⎟⎟⎟⎞ , 如果系数小于等于 0 0 0 , 该值就是无效值 , 默认为无穷大 , 不进行比较 , 选择 1 1 1 对应的基变量作为出基变量 , 查看该最小值对应的变量是 x 7 x_7 x7 , 选择该 x 7 x_7 x7 变量作为出基变量 ;
九、初始单纯形表 : 更新单纯形表
| c j c_j cj | c j c_j cj | 3 3 3 | 2 2 2 | − 1 -1 −1 | 0 0 0 | 0 0 0 | − M -M −M | − M -M −M | ||
|---|---|---|---|---|---|---|---|---|---|---|
| C B C_B CB 基变量系数 (目标函数) | X B X_B XB 基变量 | 常数 b b b | x 1 x_1 x1 | x 2 x_2 x2 | x 3 x_3 x3 | x 4 x_4 x4 | x 5 x_5 x5 | x 6 x_6 x6 | x 7 x_7 x7 | θ i \theta_i θi |
| − M -M −M ( 目标函数 x 6 x_6 x6 系数 c 6 c_6 c6 ) | x 6 x_6 x6 | 4 4 4 | − 4 -4 −4 | 3 3 3 | 1 1 1 | − 1 -1 −1 | 0 0 0 | 1 1 1 | 0 0 0 | 4 4 4 ( θ 6 \theta_6 θ6) |
| 0 0 0 ( 目标函数 x 5 x_5 x5 系数 c 5 c_5 c5) | x 5 x_5 x5 | 10 10 10 | 1 1 1 | − 1 -1 −1 | 2 2 2 | 0 0 0 | 1 1 1 | 0 0 0 | 0 0 0 | 5 5 5 ( θ 5 \theta_5 θ5 ) |
| − M -M −M ( 目标函数 x 7 x_7 x7 系数 c 7 c_7 c7) | x 7 x_7 x7 | 1 1 1 | 2 2 2 | − 2 -2 −2 | 1 1 1 | 0 0 0 | 0 0 0 | 0 0 0 | 1 1 1 | 1 1 1 ( θ 7 \theta_7 θ7 ) |
| σ j \sigma_j σj ( 检验数 ) | 3 − 2 M 3-2M 3−2M ( σ 1 \sigma_1 σ1 ) | 2 + M 2+M 2+M ( σ 2 \sigma_2 σ2 ) | − 1 + 2 M -1 + 2M −1+2M ( σ 3 \sigma_3 σ3 ) | − M -M −M ( σ 3 \sigma_3 σ3 ) | 0 0 0 | 0 0 0 | 0 0 0 |
十、第一次迭代 : 中心元变换
当前初始单纯形表 :
| c j c_j cj | c j c_j cj | 3 3 3 | 2 2 2 | − 1 -1 −1 | 0 0 0 | 0 0 0 | − M -M −M | − M -M −M | ||
|---|---|---|---|---|---|---|---|---|---|---|
| C B C_B CB 基变量系数 (目标函数) | X B X_B XB 基变量 | 常数 b b b | x 1 x_1 x1 | x 2 x_2 x2 | x 3 x_3 x3 | x 4 x_4 x4 | x 5 x_5 x5 | x 6 x_6 x6 | x 7 x_7 x7 | θ i \theta_i θi |
| − M -M −M ( 目标函数 x 6 x_6 x6 系数 c 6 c_6 c6 ) | x 6 x_6 x6 | 4 4 4 | − 4 -4 −4 | 3 3 3 | 1 1 1 | − 1 -1 −1 | 0 0 0 | 1 1 1 | 0 0 0 | 4 4 4 ( θ 6 \theta_6 θ6) |
| 0 0 0 ( 目标函数 x 5 x_5 x5 系数 c 5 c_5 c5) | x 5 x_5 x5 | 10 10 10 | 1 1 1 | − 1 -1 −1 | 2 2 2 | 0 0 0 | 1 1 1 | 0 0 0 | 0 0 0 | 5 5 5 ( θ 5 \theta_5 θ5 ) |
| − M -M −M ( 目标函数 x 7 x_7 x7 系数 c 7 c_7 c7) | x 7 x_7 x7 | 1 1 1 | 2 2 2 | − 2 -2 −2 | 1 1 1 | 0 0 0 | 0 0 0 | 0 0 0 | 1 1 1 | 1 1 1 ( θ 7 \theta_7 θ7 ) |
| σ j \sigma_j σj ( 检验数 ) | 3 − 2 M 3-2M 3−2M ( σ 1 \sigma_1 σ1 ) | 2 + M 2+M 2+M ( σ 2 \sigma_2 σ2 ) | − 1 + 2 M -1 + 2M −1+2M ( σ 3 \sigma_3 σ3 ) | − M -M −M ( σ 4 \sigma_4 σ4 ) | 0 0 0 | 0 0 0 | 0 0 0 |
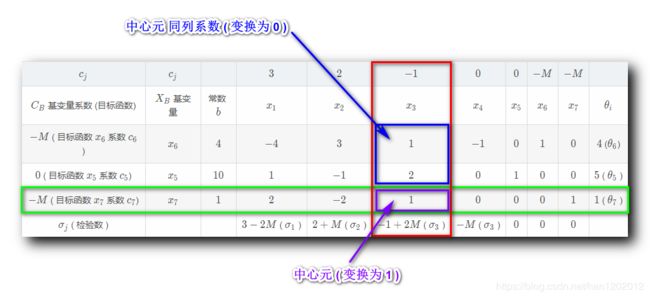
中心元 : 入基变量为 x 3 x_3 x3 , 出基变量为 x 7 x_7 x7 , 在单纯形表中 , 入基变量与出基变量相交的位置 , 称为中心元 ;
中心元变换 : 以中心元为轴 , 作系数矩阵变换 ;
- 中心元位置变换成 1 1 1 ;
- 中心元对应入基变量所在列其它位置变换为 0 0 0 ;
当前约束方程组为 :
s . t { − 4 x 1 + 3 x 2 + x 3 − x 4 + 0 x 5 + x 6 + 0 x 7 = 4 x 1 − x 2 + 2 x 3 + 0 x 4 + x 5 + 0 x 6 + 0 x 7 = 10 2 x 1 − 2 x 2 + x 3 + 0 x 4 + 0 x 5 + 0 x 6 + x 7 = 1 x j ≥ 0 ( j = 1 , 2 , 3 , 4 , 5 , 6 , 7 ) s.t\begin{cases} -4 x_1 + 3x_2 + x_3 - x_4 + 0x_5 + x_6 + 0x_7 = 4 \\\\ x_1 - x_2 + 2x_3 + 0x_4 + x_5 + 0x_6 + 0x_7 = 10 \\\\ 2x_1 - 2x_2 + x_3 + 0x_4 + 0x_5 + 0x_6 + x_7 = 1 \\\\ x_j \geq 0 \quad (j = 1 , 2 , 3, 4, 5 , 6 , 7 ) \end{cases} s.t⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧−4x1+3x2+x3−x4+0x5+x6+0x7=4x1−x2+2x3+0x4+x5+0x6+0x7=102x1−2x2+x3+0x4+0x5+0x6+x7=1xj≥0(j=1,2,3,4,5,6,7)
方程 3 3 3 变换 : 在 2 x 1 − 2 x 2 + x 3 + 0 x 4 + 0 x 5 + 0 x 6 + x 7 = 1 2x_1 - 2x_2 + x_3 + 0x_4 + 0x_5 + 0x_6 + x_7 = 1 2x1−2x2+x3+0x4+0x5+0x6+x7=1 中 , x 3 x_3 x3 的系数是中心元 , 其系数需要变换成 1 1 1 , 其本身就是 1 1 1 , 方程 3 3 3 等式不用进行变换 ;
方程 2 2 2 变换 : 将 x 1 − x 2 + 2 x 3 + 0 x 4 + x 5 + 0 x 6 + 0 x 7 = 10 x_1 - x_2 + 2x_3 + 0x_4 + x_5 + 0x_6 + 0x_7 = 10 x1−x2+2x3+0x4+x5+0x6+0x7=10 等式中 x 3 x_3 x3 的系数变为 0 0 0 , 将 方程 3 3 3 左右两端乘以 − 2 -2 −2 , 与方程 2 2 2 相加 ;
( 2 x 1 − 2 x 2 + x 3 + 0 x 4 + 0 x 5 + 0 x 6 + x 7 ) × − 2 + ( x 1 − x 2 + 2 x 3 + 0 x 4 + x 5 + 0 x 6 + 0 x 7 ) = − 2 + 10 − 3 x 1 + 3 x 2 + 0 x 3 + 0 x 4 + x 5 + 0 x 6 − 2 x 7 = 8 \begin{array}{lcl} ( 2x_1 - 2x_2 + x_3 + 0x_4 + 0x_5 + 0x_6 + x_7 ) \times -2 + (x_1 - x_2 + 2x_3 + 0x_4 + x_5 + 0x_6 + 0x_7) = -2 + 10 \\\\ -3x_1 + 3x_2 + 0x_3 + 0x_4 + x_5 + 0x_6 - 2 x_7 = 8 \end{array} (2x1−2x2+x3+0x4+0x5+0x6+x7)×−2+(x1−x2+2x3+0x4+x5+0x6+0x7)=−2+10−3x1+3x2+0x3+0x4+x5+0x6−2x7=8
方程 1 1 1 变换 : 将 − 4 x 1 + 3 x 2 + x 3 − x 4 + 0 x 5 + x 6 + 0 x 7 = 4 -4 x_1 + 3x_2 + x_3 - x_4 + 0x_5 + x_6 + 0x_7 = 4 −4x1+3x2+x3−x4+0x5+x6+0x7=4 等式中 x 3 x_3 x3 的系数变为 0 0 0 , 将 方程 3 3 3 左右两端乘以 − 1 -1 −1 , 与方程 1 1 1 相加 ;
( 2 x 1 − 2 x 2 + x 3 + 0 x 4 + 0 x 5 + 0 x 6 + x 7 ) × − 1 + ( − 4 x 1 + 3 x 2 + x 3 − x 4 + 0 x 5 + x 6 + 0 x 7 ) = − 1 + 4 − 6 x 1 + 5 x 2 + 0 x 3 − x 4 + 0 x 5 + x 6 − x 7 = 3 \begin{array}{lcl} ( 2x_1 - 2x_2 + x_3 + 0x_4 + 0x_5 + 0x_6 + x_7 ) \times -1 + (-4 x_1 + 3x_2 + x_3 - x_4 + 0x_5 + x_6 + 0x_7) = -1 + 4 \\\\ -6x_1 + 5x_2 + 0x_3 -x_4 + 0x_5 + x_6 - x_7 =3 \end{array} (2x1−2x2+x3+0x4+0x5+0x6+x7)×−1+(−4x1+3x2+x3−x4+0x5+x6+0x7)=−1+4−6x1+5x2+0x3−x4+0x5+x6−x7=3
最终方程组为 :
s . t { − 6 x 1 + 5 x 2 + 0 x 3 − x 4 + 0 x 5 + x 6 − x 7 = 3 − 3 x 1 + 3 x 2 + 0 x 3 + 0 x 4 + x 5 + 0 x 6 − 2 x 7 = 8 2 x 1 − 2 x 2 + x 3 + 0 x 4 + 0 x 5 + 0 x 6 + x 7 = 1 s.t\begin{cases} -6x_1 + 5x_2 + 0x_3 -x_4 + 0x_5 + x_6 - x_7 =3 \\\\ -3x_1 + 3x_2 + 0x_3 + 0x_4 + x_5 + 0x_6 - 2 x_7 = 8 \\\\ 2x_1 - 2x_2 + x_3 + 0x_4 + 0x_5 + 0x_6 + x_7 = 1 \end{cases} s.t⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧−6x1+5x2+0x3−x4+0x5+x6−x7=3−3x1+3x2+0x3+0x4+x5+0x6−2x7=82x1−2x2+x3+0x4+0x5+0x6+x7=1
十一、第一次迭代 : 单纯形表
x 7 x_7 x7 是后添加的人工变量 , 其取值肯定是 0 0 0 , 这里的单纯性表中 , 可以将 x 7 x_7 x7 彻底删除 , 不再使用 ;
| c j c_j cj | c j c_j cj | 3 3 3 | 2 2 2 | − 1 -1 −1 | 0 0 0 | 0 0 0 | − M -M −M | − M -M −M | ||
|---|---|---|---|---|---|---|---|---|---|---|
| C B C_B CB 基变量系数 (目标函数) | X B X_B XB 基变量 | 常数 b b b | x 1 x_1 x1 | x 2 x_2 x2 | x 3 x_3 x3 | x 4 x_4 x4 | x 5 x_5 x5 | x 6 x_6 x6 | x 7 x_7 x7 | θ i \theta_i θi |
| − M -M −M ( 目标函数 x 6 x_6 x6 系数 c 6 c_6 c6 ) | x 6 x_6 x6 | 4 4 4 | − 4 -4 −4 | 3 3 3 | 1 1 1 | − 1 -1 −1 | 0 0 0 | 1 1 1 | 0 0 0 | 4 4 4 ( θ 6 \theta_6 θ6) |
| 0 0 0 ( 目标函数 x 5 x_5 x5 系数 c 5 c_5 c5) | x 5 x_5 x5 | 10 10 10 | 1 1 1 | − 1 -1 −1 | 2 2 2 | 0 0 0 | 1 1 1 | 0 0 0 | 0 0 0 | 5 5 5 ( θ 5 \theta_5 θ5 ) |
| − M -M −M ( 目标函数 x 7 x_7 x7 系数 c 7 c_7 c7) | x 7 x_7 x7 | 1 1 1 | 2 2 2 | − 2 -2 −2 | 1 1 1 | 0 0 0 | 0 0 0 | 0 0 0 | 1 1 1 | 1 1 1 ( θ 7 \theta_7 θ7 ) |
| σ j \sigma_j σj ( 检验数 ) | 3 − 2 M 3-2M 3−2M ( σ 1 \sigma_1 σ1 ) | 2 + M 2+M 2+M ( σ 2 \sigma_2 σ2 ) | − 1 + 2 M -1 + 2M −1+2M ( σ 4 \sigma_4 σ4 ) | − M -M −M ( σ 3 \sigma_3 σ3 ) | 0 0 0 | 0 0 0 | 0 0 0 | |||
| 第二次迭代 | – | – | – | – | – | – | – | – | – | – |
| − M -M −M ( 目标函数 x 6 x_6 x6 系数 c 6 c_6 c6 ) | x 6 x_6 x6 | 3 3 3 | − 6 -6 −6 | 5 5 5 | 0 0 0 | − 1 -1 −1 | 0 0 0 | 1 1 1 | 移除 | ? ? ? ( θ 6 \theta_6 θ6) |
| 0 0 0 ( 目标函数 x 5 x_5 x5 系数 c 5 c_5 c5) | x 5 x_5 x5 | 8 8 8 | − 3 -3 −3 | 3 3 3 | 0 0 0 | 0 0 0 | 1 1 1 | 0 0 0 | 移除 | ? ? ? ( θ 5 \theta_5 θ5 ) |
| − 1 -1 −1 ( 目标函数 x 3 x_3 x3 系数 c 3 c_3 c3) | x 3 x_3 x3 | 1 1 1 | 2 2 2 | − 2 -2 −2 | 1 1 1 | 0 0 0 | 0 0 0 | 0 0 0 | 移除 | ? ? ? ( θ 3 \theta_3 θ3 ) |
| σ j \sigma_j σj ( 检验数 ) | ? ? ? ( σ 1 \sigma_1 σ1 ) | ? ? ? ( σ 2 \sigma_2 σ2 ) | 0 0 0 | ? ? ? ( σ 4 \sigma_4 σ4 ) | 0 0 0 | 0 0 0 | 移除 |
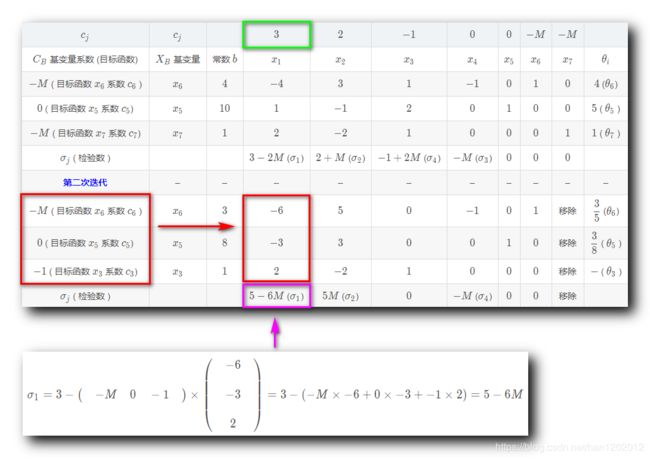
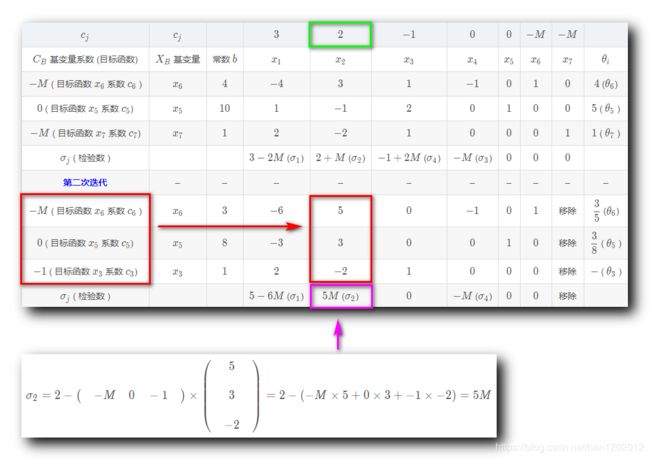
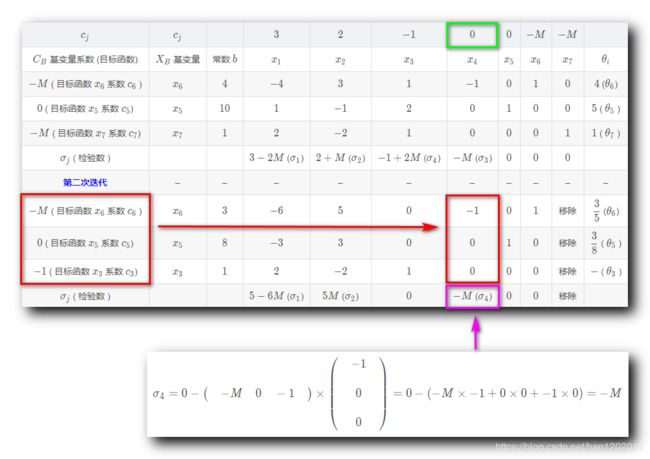
十二、第一次迭代 : 计算检验数
1 . 计算非基变量 x 1 x_1 x1 的检验数 σ 1 \sigma_1 σ1 :
σ 1 = 3 − ( − M 0 − 1 ) × ( − 6 − 3 2 ) = 3 − ( − M × − 6 + 0 × − 3 + − 1 × 2 ) = 5 − 6 M \sigma_1 = 3 - \begin{pmatrix} \quad -M \quad 0 \quad -1 \quad \\ \end{pmatrix} \times \begin{pmatrix} \quad -6 \quad \\\\ \quad -3 \quad \\\\ \quad 2 \quad \end{pmatrix} = 3- ( -M \times -6 + 0 \times -3 + -1 \times 2) =5 - 6M σ1=3−(−M0−1)×⎝⎜⎜⎜⎜⎛−6−32⎠⎟⎟⎟⎟⎞=3−(−M×−6+0×−3+−1×2)=5−6M
其中 M M M 是正无穷 + ∞ +\infin +∞ , 5 − 6 M 5 - 6M 5−6M 是负数 ;
2 . 计算非基变量 x 2 x_2 x2 的检验数 σ 2 \sigma_2 σ2 :
σ 2 = 2 − ( − M 0 − 1 ) × ( 5 3 − 2 ) = 2 − ( − M × 5 + 0 × 3 + − 1 × − 2 ) = 5 M \sigma_2 = 2 - \begin{pmatrix} \quad -M \quad 0 \quad -1 \quad \\ \end{pmatrix} \times \begin{pmatrix} \quad 5 \quad \\\\ \quad 3 \quad \\\\ \quad -2 \quad \end{pmatrix} = 2- ( -M \times 5 + 0 \times 3 + -1 \times -2) =5M σ2=2−(−M0−1)×⎝⎜⎜⎜⎜⎛53−2⎠⎟⎟⎟⎟⎞=2−(−M×5+0×3+−1×−2)=5M
其中 M M M 是正无穷 + ∞ +\infin +∞ , 5 M 5M 5M 是正数 ;
3 . 计算非基变量 x 4 x_4 x4 的检验数 σ 4 \sigma_4 σ4 :
σ 4 = 0 − ( − M 0 − 1 ) × ( − 1 0 0 ) = 0 − ( − M × − 1 + 0 × 0 + − 1 × 0 ) = − M \sigma_4 = 0 - \begin{pmatrix} \quad -M \quad 0 \quad -1 \quad \\ \end{pmatrix} \times \begin{pmatrix} \quad -1 \quad \\\\ \quad 0 \quad \\\\ \quad 0 \quad \end{pmatrix} = 0- ( -M \times -1 + 0 \times 0 + -1 \times 0 ) = -M σ4=0−(−M0−1)×⎝⎜⎜⎜⎜⎛−100⎠⎟⎟⎟⎟⎞=0−(−M×−1+0×0+−1×0)=−M
其中 M M M 是正无穷 + ∞ +\infin +∞ , − M -M −M 是负数 ;
十三、第一次迭代 : 最优解判定
根据上述三个检验数 { σ 1 = 5 − 6 M ( 负 数 ) σ 2 = 5 M ( 正 数 ) σ 4 = − M ( 负 数 ) \begin{cases} \sigma_1 = 5 - 6M \quad ( 负数 )\\\\ \sigma_2= 5M \quad ( 正数 )\\\\ \sigma_4 = -M \quad ( 负数 ) \end{cases} ⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧σ1=5−6M(负数)σ2=5M(正数)σ4=−M(负数) 的值 , 其中 σ 2 \sigma_2 σ2 检验数大于 0 0 0 , 该基可行解不是最优解 ;
只有当检验数都小于等于 0 0 0 时 , 该基可行解才是最优解 ;
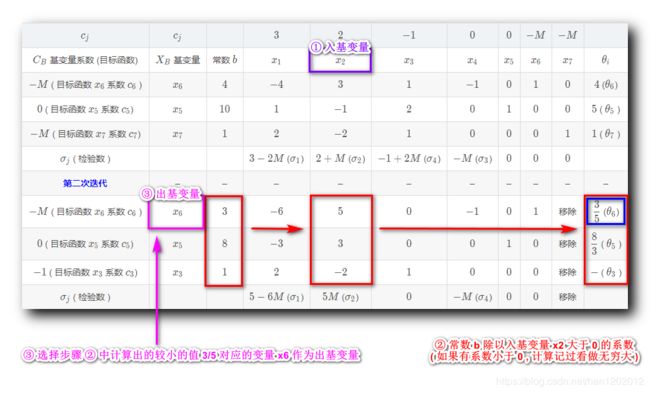
十四、第一次迭代 : 选择入基变量
根据上述三个检验数 { σ 1 = 5 − 6 M ( 负 数 ) σ 2 = 5 M ( 正 数 ) σ 4 = − M ( 负 数 ) \begin{cases} \sigma_1 = 5 - 6M \quad ( 负数 )\\\\ \sigma_2= 5M \quad ( 正数 )\\\\ \sigma_4 = -M \quad ( 负数 ) \end{cases} ⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧σ1=5−6M(负数)σ2=5M(正数)σ4=−M(负数) 的值 , 选择检验数最大的非基变量作为入基变量 , σ 2 = 5 M \sigma_2= 5M σ2=5M 最大 , 这里选择 x 2 x_2 x2 作为入基变量 ;
十五、第一次迭代 : 选择出基变量
出基变量选择 : 常数列 b = ( 3 8 1 ) b =\begin{pmatrix} \quad 3 \quad \\ \quad 8 \quad \\ \quad 1 \quad \\ \end{pmatrix} b=⎝⎛381⎠⎞ , 分别除以除以入基变量 x 2 x_2 x2 大于 0 0 0 的系数列 ( 5 3 − 2 ) \begin{pmatrix} \quad 5 \quad \\\\ \quad 3 \quad \\\\ \quad -2 \quad \end{pmatrix} ⎝⎜⎜⎜⎜⎛53−2⎠⎟⎟⎟⎟⎞ , 计算过程如下 ( 3 5 8 3 系 数 不 符 合 要 求 ) \begin{pmatrix} \quad \cfrac{3}{5} \quad \\\\ \quad \cfrac{8}{3} \quad \\\\ \quad 系数不符合要求 \quad \end{pmatrix} ⎝⎜⎜⎜⎜⎜⎜⎜⎛5338系数不符合要求⎠⎟⎟⎟⎟⎟⎟⎟⎞ , 得出结果是 ( 3 5 8 3 − ) \begin{pmatrix} \quad \cfrac{3}{5} \quad \\\\ \quad \cfrac{8}{3} \quad \\\\ \quad - \quad \end{pmatrix} ⎝⎜⎜⎜⎜⎜⎜⎜⎛5338−⎠⎟⎟⎟⎟⎟⎟⎟⎞ , 如果系数小于等于 0 0 0 , 该值就是无效值 , 默认为无穷大 , 不进行比较 , 选择 3 5 \cfrac{3}{5} 53 对应的基变量作为出基变量 , 查看该最小值对应的变量是 x 6 x_6 x6 , 选择该 x 6 x_6 x6 变量作为出基变量 ;
十六、第一次迭代 : 更新单纯形表
x 7 x_7 x7 是后添加的人工变量 , 其取值肯定是 0 0 0 , 这里的单纯性表中 , 可以将 x 7 x_7 x7 彻底删除 , 不再使用 ;
| c j c_j cj | c j c_j cj | 3 3 3 | 2 2 2 | − 1 -1 −1 | 0 0 0 | 0 0 0 | − M -M −M | − M -M −M | ||
|---|---|---|---|---|---|---|---|---|---|---|
| C B C_B CB 基变量系数 (目标函数) | X B X_B XB 基变量 | 常数 b b b | x 1 x_1 x1 | x 2 x_2 x2 | x 3 x_3 x3 | x 4 x_4 x4 | x 5 x_5 x5 | x 6 x_6 x6 | x 7 x_7 x7 | θ i \theta_i θi |
| − M -M −M ( 目标函数 x 6 x_6 x6 系数 c 6 c_6 c6 ) | x 6 x_6 x6 | 4 4 4 | − 4 -4 −4 | 3 3 3 | 1 1 1 | − 1 -1 −1 | 0 0 0 | 1 1 1 | 0 0 0 | 4 4 4 ( θ 6 \theta_6 θ6) |
| 0 0 0 ( 目标函数 x 5 x_5 x5 系数 c 5 c_5 c5) | x 5 x_5 x5 | 10 10 10 | 1 1 1 | − 1 -1 −1 | 2 2 2 | 0 0 0 | 1 1 1 | 0 0 0 | 0 0 0 | 5 5 5 ( θ 5 \theta_5 θ5 ) |
| − M -M −M ( 目标函数 x 7 x_7 x7 系数 c 7 c_7 c7) | x 7 x_7 x7 | 1 1 1 | 2 2 2 | − 2 -2 −2 | 1 1 1 |