Pointproofs: Aggregating Proofs for Multiple Vector Commitments 学习笔记1

1. 背景知识

Alogrand团队Gorbunov等人2020年论文《Pointproofs: Aggregating Proofs for Multiple Vector Commitments》，配套的代码实现参见：https://github.com/algorand/pointproofs

在该论文中，实现了：

• Pointproofs —— a new vector commitment scheme that supports non-interactive aggregation of proofs across multiple commitments。允许任何第三方 aggregate a collection of proofs with respect to different, independently computed commitments into a single proof represented by an elliptic curve point of 48-bytes。
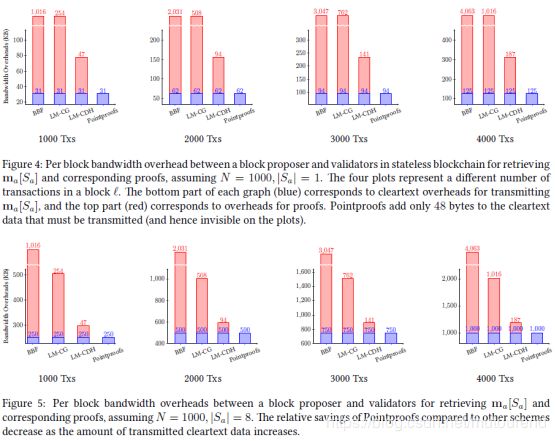
• 将Pointproofs用于blockchain smart contract。相比于之前的vector commitment方案，Pointproofs可将传输一个区块交易所需的带宽开销降低至少60%。
• 以单线程运行时，generate a proof for 8 values with respect to one commitment的时间为0.08s，aggregate 4000 such proofs across multiple commitments into one proof的时间为0.25s，verify the aggregated proof的时间为23s（0.7ms per value proven）。

Vector commitment可用于减少存储空间：instead of storing a vector of values, one can store only the commitment and receive the values together with their proofs as needed。

Vector commitment可让application 在storage of all value和 bandwidth taken up by revealed values and proofs 之间进行取舍平衡。
为了在减少存储空间的同时尽可能减少带宽，需要 reduce the proof size。但是，由于需要满足cryptographically hard to forge的要求，单个proof的size cannot be reduced too far。改进的方式可为：

• 在单个proof中支持reveal multiple values。最短的单个proof size实现可参见Russell W. F. Lai 和 Giulio Malavolta 在Crypto 2019上发表的论文《Subvector Commitments with Application to Succinct Arguments》中5.2节构建的subvector commitment from Cube Diffie-Hellman Assumption：a proof takes up only 48 bytes (for typical parameter values at conjectured 128-bit security) regardless of how many elements of the vector are being revealed。（参见博客 Subvector Commitments with Application to Succinct Arguments学习笔记）
• 在分布式应用中，存在大量来源不同的commitments/values/proofs，它们相互 not aware of each other’s data。此时存在以下两个问题：
  1）不存在可produce a single proof for all the values的单一实体；
  2）proofs需要于多个不同的commitments关联。
  Pointproofs可有效解决以上问题：a user can independently commit to her variables and provide short proofs for any subset of them; any third party can non-interactively aggregate multiple proofs with respect to different commitments into a single short proof。

Boneh等人2019年论文《Batching techniques for accumulators with applications to IOPs and stateless blockchains》可实现dynamic aggregation for proofs in a single (the same) commitment —— aggregate proofs for elements of a vector into a single proof for a subvector。（参见博客 密码学累加器cryptographic accumulator）
而在本论文中，Gorbunov等人实现了跨多个commitments的aggregate proofs。
具体的各方案对比为：

在本论文中，Gorbunov等人的主要贡献为：

• 实现了proofs for individual elements of a single vector commitment can be aggregated by any third party into a single proof for the subvector；

• 实现了proofs for subvectors of multiple commitments can be aggregated by any third party into a single proof for the multiple subvectors。

• 在实现aggregation的同时，也提供了hiding属性。

• 在Libert和Yung 2010年论文《Concise mercurial vector commitments and independent zero-knowledge sets with short proofs》构建的vector commitment基础上，增加了same-commitment aggregation和cross-commitment aggregation，从而实现了Pointproofs。
  1）与此类似，Pointproofs的public parameter size is linear in the size of the committed vector（可将long vector切分为多个短的vectors，多个短的vectors的proofs可以aggregate，但是commitments不能aggregate，从而缩短了public parameter size，但是增加了total size of the commitments）；
  2）与此类似，Pointproofs也基于$q$-type assumption。In order to prove security of aggregation, we have to work in the algebraic group model and the random oracle model. We can reduce these assumptions by lowering efficiency and/or security requirements.

• Pointproofs生成的proof为single point on a pairing-friendly curve (48 bytes at 128-bit security)，无论是single value for a single commitment，subvector of values for a single commitment，还是set of subvectors for multiple commitments。

• Pointproofs中实现了支持aggregation的hiding属性，仅需增加an additional exponentiation，commitment size和proof size均无需增加。而Dario Catalano 和 Dario Fiore 2013年论文《Vector Commitments and their Applications》中提到的给Vector commitment加hiding属性的方法为：add an inner layer of hiding commitments to individual values —— first commit to each message separately using a standard commitment scheme, then apply the VC to the obtained sequence of commitments。但是该方式无法automatically extend to aggregatable vector commitments，因为proofs for the inner layer are not automatically aggregatable。

• Pointproofs可用于reduce storage requirements for blockchains。主要针对smart contract智能合约场景。假设一个智能合约有多个变量，所有变量当前值$(m_1,\cdots ,m_N)$ are committed to a single vector commitment $C$，每个智能合约有一个commitment。
  为了与智能合约交互，one provides a 480byte proof $ \hat{\pi}$ of the current values of the variables needed for the transaction，transaction成功执行后可能会更新这些变量值。当存在多个智能合约时，cross-commitment aggregation允许compress multiple proofs ${\hat{\pi }}_1,\cdots ,{\hat{\pi }}_l$ into a single 48-byte proof $\pi$。从而可从根本上消除the bandwidth overhead due to proofs in a proposed block。
  将Pointproofs用于智能合约存储时，针对$10^8$千万级accounts，可将validators’ storage requirements降为4.5GB，assuming one open value per transaction 的情况下，仅需增加31KB per block overhead for 1000 transactions。

• Pointproofs 代码实现https://github.com/algorand/pointproofs 中的实际性能表现为：针对a commitment for 1000 variables of a smart contract at 128-bit security level，生成任意subvector proof的时间为54~123ms；a block proposer对所有proofs进行cross-commitment aggregate的时间约为0.07ms per proof；存储了commitments 的 validator verify the aggregated proofs in a block的时间约为 0.7~1.9ms per value verified；为表示变量值的更新（通过交易执行），需要update commitments的时间约为0.2~0.3ms per variable updated。

cross-commitment aggregation of proofs可用于很多场景，如：

• signature aggregation：compress multiple signatures produced by different users into a short signature。如Jae Hyun Ahn等人2010年论文《Synchronized aggregate signatures: new definitions, constructions and applications》中介绍的sensor networks，KyleBrogle等人2012年论文《Sequential aggregate signatures with lazy verification from trapdoor permutations - (extended abstract)》中介绍的internet routing以及Drijvers等人2020年论文《Pixel: Multi-signatures for consensus》中介绍的POS (Proof-of-Stake) 共识。Aggregating commitment proofs is a natural counterpart to aggregating signatures。
• 多个用户或实体分别独立commit to their databases of records（如public keys, healthcare records, transactions等），然后同时produce proofs to reveal several committed values。在这种场景下，cross-commitment aggregation可用于减少带宽。

vector commitment的相关工作：

• 正式定义了vector commitments：Libert和Yung 2010年论文《Concise mercurial vector commitments and independent zero-knowledge sets with short proofs》，以及Dario Catalano 和 Dario Fiore 2013年论文《Vector Commitments and their Applications》。
• 实现了constant-size proofs for a subvector of values：Kate等人2010年论文《Constant-size commitments to polynomials and their applications》，以及Thakur 2019年论文《Batching non-membership proofs with bilinear accumulators》。
  但是Kate等人2010年论文《Constant-size commitments to polynomials and their applications》第3.4节定义的binding notion is not strong enough to preclude openings to two inconsistent subvectors。
  而Libert和Yung 2010年论文《Concise mercurial vector commitments and independent zero-knowledge sets with short proofs》， Dario Catalano 和 Dario Fiore 2013年论文《Vector Commitments and their Applications》，Benoˆıt Libert, Somindu C. Ramanna 和 Moti Yung 2016年论文 《Functional Commitment Schemes: From Polynomial Commitments to Pairing-Based Accumulators from Simple Assumptions》，以及Chepurnoy等人2018年论文《Edrax: A cryptocurrency with stateless transaction validation》，这些论文中的vector commitment无法实现constant-size proofs for multiple values。
• pairing-based vector commitments：Dario Catalano 和 Dario Fiore 2013年论文《Vector Commitments and their Applications》，Benoˆıt Libert, Somindu C. Ramanna 和 Moti Yung 2016年论文 《Functional Commitment Schemes: From Polynomial Commitments to Pairing-Based Accumulators from Simple Assumptions》，以及Russell W. F. Lai 和 Giulio Malavolta 在Crypto 2019上发表的论文《Subvector Commitments with Application to Succinct Arguments》。
• polynomial commitments：始于Kate等人2010年论文《Constant-size commitments to polynomials and their applications》，overview信息可参看Benedikt B¨unz等人2019年论文《Proofs for inner pairing products and applications》。
  在Boneh等人2020年论文《Efficient polynomial commitment schemes for multiple points and polynomials》中实现了polynomial commitments with batch opening和vector commitments with aggregation，但是其效率要低于本论文实现。

1.1 一些定义

• Notation：
  

• The Algebraic Group Model(AGM) ：即adversary输出的group element值应基于其收到的group element进行有效的group operation计算得出的，而不是随意创造的。
  Suppose adversary is given group elements $X_1,\cdots ,X_N\in {\mathbb{G}}_1$. Then, for every group element $Z\in {\mathbb{G}}_1$ that the adversary outputs, it must also ouput $z_1,\cdots ,z_N\in {\mathbb{Z}}_p$ such that $Z={\prod }_{i=1}^N{X}_i^{z_i}$.

• security assumption：在bilinear pairing group中求解$l$-wBDHE（weak bilinear Diffie-Hellman exponent problem）很难，即对任意的$\alpha \leftarrow {\mathbb{Z}}_p$已知$g_1^{\alpha },g_1^{({\alpha }^2)},\cdots ,g_1^{({\alpha }^l)},g_1^{({\alpha }^{l+2})},\cdots ,g_1^{({\alpha }^{3l})},g_2^{\alpha },g_2^{({\alpha }^2)},\cdots ,g_2^{({\alpha }^l)}$
  求解$g_1^{({\alpha }^{l+1})}$很难。
  对于BLS12-381 pairing-friendly curve with $l=32$，当前best attack has complexity $2^{112}$。

• The Random Oracle Model(ROM)：本文的security proofs are in the random oracle model。在本文model a cryptographic hash function as a truly random function, accessible to all parties only via oracle queries。本文使用了两个random oracles $H$和$H^{\prime }$，both with output space ${\mathbb{Z}}_p$。

2. vector commitment

采用与Libert和Yung 2010年论文《Concise mercurial vector commitments and independent zero-knowledge sets with short proofs》类似的思路，基于非对称bilinear pairing group，相应的实现细节为：

• Setup: Let $({\mathbb{G}}_1,{\mathbb{G}}_2,{\mathbb{G}}_T)$ be a group of prime order $p$，along with pairing $e:{\mathbb{G}}_1\times {\mathbb{G}}_2\to {\mathbb{G}}_T$ and generators $g_1,g_2,g_T=e(g_1,g_2)$ for ${\mathbb{G}}_1,{\mathbb{G}}_2,{\mathbb{G}}_T$ respectively. Let $\alpha \in {\mathbb{Z}}_p$ be a secret value (known to no one after the initial generation of public parameters). The pulic parameters are given by $2N-1$ values in ${\mathbb{G}}_1$, $N$ values in ${\mathbb{G}}_2$, and one value in ${\mathbb{G}}_T$(该值易于计算获得，如$g_T^{{\alpha }^{N+1}}=e(g_1^{\alpha },g_2^{{\alpha }^N})=e(g_1,g_2{)}^{{\alpha }^{N+1}}$)：【注意$g_1^{{\alpha }^{N+1}}$不应包含在public parameters中，否则Prover可伪造证明。】
  $g_1^{\alpha },\cdots ,g_1^{{\alpha }^N},g_1^{{\alpha }^{N+2}},\cdots ,g_1^{{\alpha }^{2N}};g_2^{\alpha },\cdots ,g_2^{{\alpha }^N};g_T^{{\alpha }^{N+1}}$

• Commit：对vector $m=(m_1,\cdots ,m_N)\in {\mathbb{Z}}_p^N$，
  $C=g_1^{{\sum }_{i=1}^N{m}_i{\alpha }^i}$

• Prove：reveal $m_i$，
  ${\pi }_i=g_1^{{\sum }_{j\ne i}{m}_j{\alpha }^{N+1-i+j}}=(C/g_1^{m_i{\alpha }^i}{)}^{{\alpha }^{N+1-i}}$

• Verify：
  $e(C,g_2^{{\alpha }^{N+1-i}})=e({\pi }_i,g_2)\cdot g_T^{m_i{\alpha }^{N+1}}$

2.1 支持aggregation的vector commitment思路集锦

为了实现reveal multiple values $m_i:i\in S$ (其中$S\subseteq [N]$) for a single commitment $C$ via a very short proof ${\pi }_S$。

• 思路一：
  直接计算${\pi }_S={\prod }_{i\in S}{\pi }_i$，然后验证$e(C,{\prod }_{i\in S}{g}_2^{{\alpha }^{N+1-i}})=e({\pi }_S,g_2)\cdot g_T^{{\alpha }^{N+1}{\sum }_{i\in S}{m}_i}$。
  该方式不安全，若open $S=1,2$，可commit to $(m_1,m_2)=(1,3)$而open为$(m_1,m_2)=(2,2)$，违反了binding属性（只bound to ${\sum }_{i\in S}{m}_i$，而不是$\{m_i:i\in S\}$中的每一个值。）。
  同时，还需要防止inconsistnent reveals for possibly two different sets，如分别open $(m_1,m_2)$为$(1,3)$，$(m_2,m_3)$为$(2,1)$的情况是不允许的。

• 思路二：实现same-commitment aggregation
  在verification方程式中引入“随机”scalars $t_i$，
  $e(C,{\prod }_{i\in S}{g}_2^{{\alpha }^{N+1-i}{t}_i})=e({\pi }_S,g_2)\cdot g_T^{{\alpha }^{N+1}{\sum }_{i\in S}{m}_i{t}_i}$
  aggregated proof ${\pi }_S={\prod }_{i\in S}{\pi }_i^{t_i}$
  scalars $t_i$的值可通过applying a hash function $H$ on some carefully chosen inputs depending on $C,S,\{m_i:i\in S\}$。类似的思路在Boneh等人2018年论文《Compact multi-signatures for smaller blockchains》的aggregating signatures中有提及。
  怎样选择$t_i$来保证binding属性呢？若$t_i\leftarrow {\mathbb{Z}}_p$为indeed random，则可保证$Pr[{\sum }_{i\in S}{m}_i{t}_i={\sum }_{i\in S}{m}_i^{\prime }{t}_i^{\prime }]=1/p$，即对同一位置open为两个不同值的概率可忽略。
  可将hash function $H$ 看成是a random oracle。同时，还需要restrict the adversary to the so-called algebraic group model，以便可express adversarially generated commitments $C$ in terms of public parameters。

• 思路三：实现cross-commitment aggregation
  对多个不同的vector进行commit，第$j$个vector 可表示为 $m_j=(m_{j,1},\cdots ,m_{j,N})$，对应的commitment为 $C_j$，对set $S_j$的open proof为${\hat{\pi }}_j$，则满足：
  $e(C_j,{\prod }_{i\in S_j}{g}_2^{{\alpha }^{N+1-i}{t}_{j,i}})=e({\hat{\pi }}_j,g_2)\cdot g_T^{{\alpha }^{N+1}{\sum }_{i\in S_j}{m}_{j,i}{t}_{j,i}}$
  若直接将多个vector对应的verification equation都一起相乘，则有：
  ${\prod }_{j}e(C_j,{\prod }_{i\in S_j}{g}_2^{{\alpha }^{N+1-i}{t}_{j,i}})=e({\prod }_j{\hat{\pi }}_j,g_2)\cdot g_T^{{\alpha }^{N+1}{\sum }_j{\sum }_{i\in S_j}{m}_{j,i}{t}_{j,i}}$
  与思路一类似，上述方式是不安全的，需要再引入额外的random scalars $t_j^{\prime }$，相应的aggregated proof为$\pi ={\prod }_j{\widehat{{\pi }_j}}^{t_j^{\prime }}$，对应的verification equation调整为：
  ${\prod }_{j}e(C_j,{\prod }_{i\in S_j}{g}_2^{{\alpha }^{N+1-i}{t}_{j,i}}{)}^{t_j^{\prime }}=e(\pi ,g_2)\cdot g_T^{{\alpha }^{N+1}{\sum }_j{\sum }_{i\in S_j}{m}_{j,i}{t}_{j,i}{t}_j^{\prime }}$

2.2 Same-commitment aggregation

首先考虑的是aggregation of proofs for a single commitment。
基本的算法包括Setup, Commit, UpdateCommit, Aggregate, Verify：

• $pp\leftarrow Setup(1^{\lambda },1^N)$：输出public parameters，支持的vector 长度为$N$。
• $C\leftarrow Commit(m;r)$：输入为vector $m\in M^N$和randomness $r$，输出为commitment $C$。
• $C^{\prime }\leftarrow UpdateCommit(C,S,m[S],m^{\prime }[S])$：输入为commitment $C$，待更新的位置集$S$，将待更新位置集内数据由$m[S]$更新为$m^{\prime }[S]$后，对应新的commitment $C^{\prime }$。
• ${\pi }_i\leftarrow Prove(i,m,r)$：open位置$i$对应的proof，输入为待open位置$i\in [N]$和$(m,r)$，输出为proof ${\pi }_i$。【应该还有一个输出$m_i$，对应open位置$i$的具体值】
• $\hat{\pi }\leftarrow Aggregate(C,S,m[S],\{{\pi }_i:i\in S\})$：输入为commitment $C$，open位置集$S\subseteq [N]$，每个位置对应的proof $\{\pi :i\in S\}$，输出为aggregated proof $\hat{\pi }$。
• $b\leftarrow Verify(C,S,m[S],\hat{\pi })$：输入为commitment $C$ ，open位置集$S\subseteq [N]$，open信息$m[S]$，aggregated proof $\hat{\pi }$，输出为$b$，0表示拒绝，1表示接受。

本论文中，为了具有通用性，定义的Verify算法总是针对的aggregated proof，哪怕仅仅open了1个位置。同时，上述定义是调用多次Prove算法生成单个位置的proof然后调用一次Aggregated算法生成aggregated proof，可能存在其它算法可直接生成aggregated proof从而提升performance，但是并不影响定义。上述定义中，若commitment updated了，需调用Prove重新生成新的proof，可能存在效率更高的updateproof算法直接update existing proof。（如博客 Vector Commitments and their Applications学习笔记 中提到的ProofUpdate算法）

整个流程应关注如下属性：

• Correctness of opening。即保证正确的proof aggregated后可100%验证通过。
  
• Correctness of updates。即保证对老的commitment进行update操作的输出值应与直接多新的vector进行commit的输出值一致。【有个typo？】
  
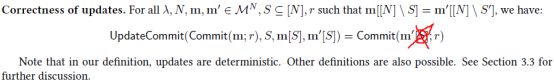
• Binding。即对同一commitment，若open不同的位置集合，应保证集合之间的交集应具有一致性，防止inconsistnent reveals for possibly two different sets。【具体见论文4.3节证明——Proof of binding for same-commitment aggregation。】
  

具体的实现可为：

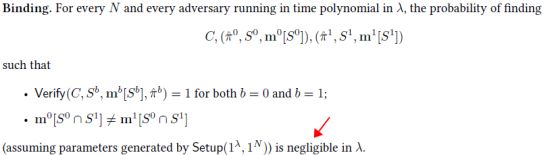
上述具体实现中，可从如下维度优化：

• Setup可通过多方安全计算或private communication等方式来高效安全实现。
• 假设$nz(m)$表示the number of non-zero entries in the vector $m$，则Commit运算需要$nz(m)$次${\mathbb{G}}_1$ exponentiation计算，Prove比Commit运算少1次。同时，可通过Pippenger等算法，计算products of exponentiations的效率要高于分别计算exponentiations。
• 实际计算same-commitment aggregated proof $\hat{\pi }$时，若$S$ is known inadvance，则可不用单独先多次调用Prove生成${\pi }_i$再Aggregate，可将两个算法合并直接生成aggregated proof，效率更高：
  
• Verify时，${\mathbb{G}}_1$域内的运算效率>${\mathbb{G}}_2$>${\mathbb{G}}_T$，计算$r=({\sum }_{i\in S}{m}_i{t}_i{)}^{-1}modp$，将${\mathbb{G}}_T$域内的运算转移到${\mathbb{G}}_1$域内，Verify的公式变更为：
  
  而a product of two pairings can be computed considerably faster than two separate pairings (because the time-consuming final exponentiation needs to be performed only once)。
  同时，当$|S|=1$，即只open 1个位置时，可设置$t_i=1$，这样可将${\mathbb{G}}_2$域内的运算转移到${\mathbb{G}}_1$域内，即上述公式第一项可为$e(C^r,g_2^{{\alpha }^{N+1-i}})$。
• 当$|S|=1$，即只open 1个位置时，可设置$t_i=1$，相当于不需要执行Aggregate运算，直接设置$\hat{\pi }={\pi }_i$。

具体各算法环节的运算复杂度为：

2.3 Cross-commitment aggregation

考虑的是aggregation of proofs across $l$ commitments。
在Same-commitment aggregation的基础上，增加了两组算法AggregateAcross和VerifyAcross：

• $\pi \leftarrow AggregateAcross(\{C_j,S_j,m_j[S_j],\widehat{{\pi }_j}{\}}_{j\in [l]})$：输入为 $l$ 组 $(\{C_j,S_j,m_j[S_j]{\}}_{j\in [l]})$和相应的same-commitment-aggregated proofs $\{\widehat{{\pi }_j}{\}}_{j\in [l]}$（通过上面的Aggregate算法获得），输出为跨commitment的aggregated proof $\pi$。
• $b\leftarrow VerifyAcross(\{C_j,S_j,m_j[S_j]{\}}_{j\in [l]},\pi )$：输入为$l$ 组 $(\{C_j,S_j,m_j[S_j]{\}}_{j\in [l]})$和cross-commitment-aggregated proof $\pi$，用于验证$C_j$ is a commitment to a message vector consistent with $m_j[S_j]$ for all $j\in [l]$。

与Same-commitment aggregation类似，也需要满足Correctness of opening属性。

Cross-commitment aggregation的binding属性以实际场景举例：【具体见论文4.4节证明——Proof of binding for cross-commitment aggregation。】
存在两组commitments，第一组（第一次）有$l^0$个不同的commitments，如包含了vectors $x,z$；第二组（第二次）有$l^1$个不同的commitments，如包含了vectors $y,x.z$。
所谓的Cross-commitment aggregation的binding属性是指，若第一次cross-commitment-aggregated proof ${\pi }^0$ 和 第二次的${\pi }^1$均VerifyAcross 验证成功，以$x$为例，第一次对应的commitment为$C_{j^0}^0$，open位置集合为$S_{j^0}^0$；第二次对用的为$C_{j^1}^1，S_{j^1}^1$，binding属性要求两次open的交集应具有一致性。
若an opening is inconsistent with a same-commitment opening，则将其和其它commitment openings 聚合在一起的cross-commitment aggregated proof应验证失败。
？即cross-commitment aggregation的binding属性要求要强于same-commitment aggregation 中的binding属性。若cross-commitment中的任一commitment的binding属性有问题，则相应的cross-commitment aggregation proof应验证失败。

特殊地，当$l^0=l^1=1$时，其实就是same-commitment。

具体的实现可为：

借助2.2节中的优化思路，可做如下调整：

2.4 hiding属性的实现

本文考虑的是simulation-based statistical security——存在efficient randomized simulator $(Setup\ast ,Commit\ast ,Prove\ast )$，其中：

• $Setup\ast$：输出$pp$和trapdoor $td$。
• $Commit\ast (;r)$；除了随机值$r$外无其它输入，输出为a random fake commitment $C$。【fake commitment】
• $Prove\ast$：基于trapdoor $td$，fake $C$, index $i$, value $m_i$来生成a fake proof $\pi$。【fake proof】

其核心思想为以上算法生成的fake proofs应statistically indistinguishable from real ones, even given the commitments, and even if the committed messages are chosen adversarially。
fake commitment和fake proof中除了要open的信息外，应leak no information about other messages。

举例为：

• 真实的stateful oracle $O-real(pp)$：计算$Commit(m_j;r_j)$，$Prove(i,m_j,r_j)$；
• 仿真的stateful oracle $O-sim(pp,td)$：计算$Commit\ast (;r_j)$，$Prove\ast (td,r_j,i,(m_j{)}_i)$。【为实现hiding属性，很关键的一点是$Commit\ast$不获取$m_j$的任何信息，而$Prove\ast$中仅获取要open的信息$(m_j{)}_i$，除待open位置之外其它的信息均不获取。】

Hiding属性要求基于真实的stateful oracle $O-real(pp)$和仿真的stateful oracle $O-sim(pp,td)$的输出分布的差异性应可忽略。

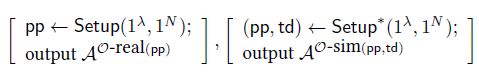
当进行update操作时，由于$C^{\prime }\leftarrow UpdateCommit(C,S,m[S],m^{\prime }[S])$是确定性的，若使用相同的randomness，通过$C$与$C^{\prime }$之间的关系会reveal $m$与$m^{\prime }$之间的关系。可以在UpdateCommit之后再增加rerandomization处理来hide this relationship。本文方案支持rerandomization操作。【commitment can be rerandomized via multiplication by $(g_1^{{\alpha }^N}{)}^{r^{\prime }}$.】

实际hiding属性的实现采用与Benoît Libert和Moti Yung 2010年论文《Concise Mercurial Vector Commitments and Independent Zero-Knowledge Sets with Short Proofs》中类似的方式——在Commit时引入随机值$g^{\gamma }$。
加入hiding元素后，具体的算法调整如下：

3. Pointproofs在区块链中的应用

Blockchain：is an append-only public ledger that consists of blocks, with every block containing some number of transactions.
区块链中最根本的问题是对新区块达成共识，共识的过程包括：

• proposer：propose a block。
• validators：verify the transactions included in the proposed block are valid。【validators的产生可由POS选举或POW中的self-selected方式产生。】

传统的方式validator需要维护整个state账本，存在存储压力问题。
在[ST99, Mil12, Whi15, Tod16,But17, Dra17, RMCI17, CPZ18, BBF19]等很多论文中，都提议validator store commitments to vectors of relevant values instead of the values themselves。基于此提议实现的可称为stateless client或者stateless blockchain。相应的，transactions中需要包含：

• the values on which they depend；
• the proofs of correctness of these values with respect to the commitments stored by the validators (which the validators would update for successful transactions)。

该模式需要在storage，bandwidth和computation之间做取舍平衡。理想的情况应该是具有small commitments and proof sizes and add little computation and bandwidth overheads to the validators。

简单的transaction，类似于比特币账号之间的转账；
复杂的transaction，是基于智能合约的。

现有各方案在解决storage方面的表现对比：【若validator直接存储明文，当需存储$10^8$个account的状态信息时，需要的存储空间将近3TB；Pointproofs中若引入central entity，对整个系统维护一个commitment，而不是为每个account维护一个commitment，但是没有意义，当$10^8$个account时，仅需4.5GB已经足够小了，没必要再引入中心化的机制。】

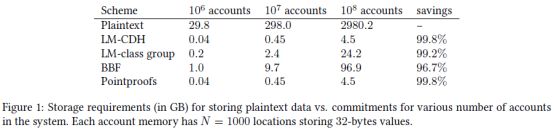
当由1000个256-bit message时，各vector commitment方案的参数：

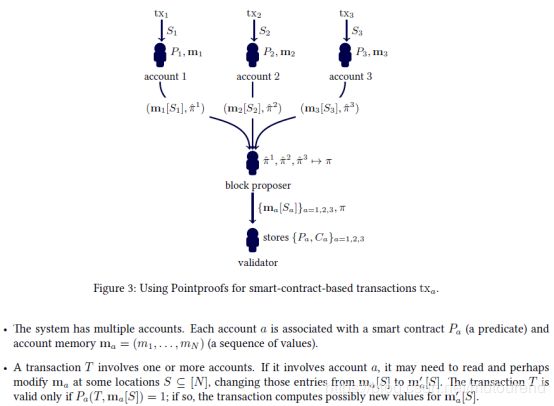
将Pointproofs用于smart-contract-based的transaction：

详细的实现流程为：

现有各方案性能对比：

Pointproofs Prove、Aggregate、Verify、AggregateAcross等基础算法的性能表现为：