区块链共识机制的博弈论思想和概率论模型
引言
我们知道,区块链是一种去中心化的数据库,没有中心化机构,所以在进行价值转移、信息传递的过程中,需要解决所有记账节点上的一致性和正确性问题。我们需要一种多方协作的机制,协调参与多方达成统一的唯一结果,且保证此过程难以被欺骗,来保证系统的稳定运行。所以,共识模型也是区块链中必不可少的重要组成部分。今天稍微了解了一下区块链共识模型里体现的的博弈论思想,分享一下。
- 拥有记账权的人更倾向在维护整个体系过程中获利(纳什均衡(Nash Equilibrium)+帕累托最优(Pareto Efficiency))
- 使用网络的人需要付出一定的成本(手续费、计算费)以免滥用
- 少数人作恶的成功几率很低,参考赌徒破产问题(Gambler‘s Ruin problem)
- 只有极端势力才有可能不顾一切的颠覆这个体系
- 整个局势不存在“确定性”,一直在动态的多方博弈
纳什均衡 Nash Equilibrium
纳什均衡中博弈的最优结果是没有一方有偏离初始策略的动机:即考虑了对手的选择后,没有任何一方有偏离自己最初选择的动机。在纳什均衡下,假设其他玩家保持策略不变,一个玩家不会从偏离最初选择的策略中获得任何好处。
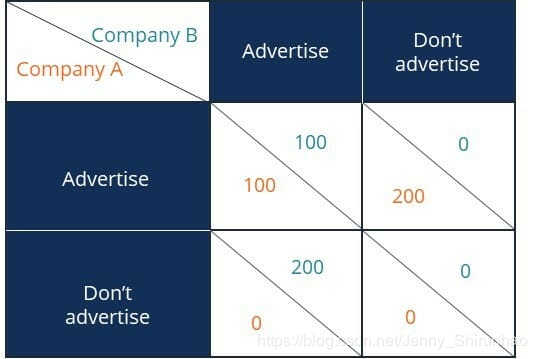
**举例:**有A和B两家公司,现在两家公司均考虑是否为其新产品投放广告。如果两家公司都投放广告,那么两家公司的新增受益均为100;若A公司选择投放广告而B公司不投放广告,那么A公司的收益为200,反之B公司收益200;若两家公司都不投放广告,那么两家公司的受益均为0,即如下表所示。
显然,该博弈的最终结果是A公司和B公司均会投放广告,因为对于任意一家公司而言,无论对面公司的选择是什么,投放广告的受益均大于不投放广告的受益。
帕累托最优 Pareto Efficiency
帕累托最优是一种经济状态,在该状态下,无法将资源进行重新分配从而使得一个个体更好而没有一个个体更糟,即,使一个个体变得更好的情况下一定会使至少一个个体变得更糟。在帕累托最优状态下,资源以最有效的方式进行分配。
为了更好的理解帕累托最优,需要引入一个新的概念——帕累托改进。
**帕累托改进(Pareto Improvement):**如果存在另一种分配,其中一个人更富有,而没有一个人更穷,那么资源分配就是帕累托改进。
如果一个资源的分配不存在帕累托改进,那么该资源的分配就是帕累托最优的。
考虑下图的生产可能性边界(production - possibilities Frontier),x轴的是物品A的输出,y轴的是物品B的输出。A、B、C、D四个点中C和D点是帕累托最优的点。因为只有C点和D点不存在帕累托改进,即不存在物品A增加的情况下物品B不减少的可能。
A同学爱吃苹果胜过爱吃橘子,B同学对苹果或橘子没有特殊的偏爱。现在有一个苹果一个橘子,怎么样的分配才是最有效的呢?
这个问题的答案不需要了解博弈学知识也可以轻松给出:给A同学苹果,给B同学橘子。
用帕累托最优来解释就是:当把苹果分给A,橘子分给B时,不存在另一种分配,使得其中一个人满意值更高的情况下,另一个人的满意值不会下降,不存在帕累托改进,即该资源分配的状态是帕累托最优状态。
赌徒破产问题 Gambler‘s Ruin problem
赌徒破产问题实际是一个概率学问题。假设一个赌徒初始有 i i i 元,每次参与赌博赢的概率为 p p p ,每次赢之后会获得1元,输掉之后资产会减少1元,且每次为独立事件,那么这个赌徒在破产前赢得 N N N 元的概率为多少?
我们认为赌徒在破产前赢得 N N N 元为赢得赌博游戏,赌徒破产为失败。
假设该赌徒经过 n n n 次赌博后的资产为 R n R_n Rn,第 k k k 次赌博的盈利记为 δ k \delta _k δk,需要注意 P ( δ k = 1 ) = p , P ( δ k = − 1 ) = 1 − p P(\delta_k=1)=p,P(\delta_k=-1)=1-p P(δk=1)=p,P(δk=−1)=1−p ,那么我们可以得到
R n = i + δ 1 + ⋯ + δ n , R 0 = i R_n=i+\delta_1+\dots+\delta_n,R_0=i Rn=i+δ1+⋯+δn,R0=i
因为当 R n = 0 R_n=0 Rn=0 或 R n = N R_n=N Rn=N 时赌博游戏结束,记游戏结束的时间为:
τ i = m i n { n ∣ n ≥ 0 , R n ∈ { 0 , N } , R 0 = i } \tau_i=min\{n|n\geq0,R_n\in \{0,N\},R_0=i\} τi=min{n∣n≥0,Rn∈{0,N},R0=i}
令 P i = P ( R τ i = N ) P_i=P(R_{\tau_i}=N) Pi=P(Rτi=N) 为赌徒以初始资产 i i i 赢得 N N N 元的概率,显然 P 0 = 0 P_0 = 0 P0=0, P N = 1 P_N=1 PN=1。
假设 δ 1 = 1 \delta_1=1 δ1=1,那么赌徒的总资产为 R 1 = i + 1 R_1=i+1 R1=i+1,根据马尔科夫性质(Markov property),当前赌徒赢得赌博游戏的概率为 P i + 1 P_{i+1} Pi+1;同样的,如果 δ i = − 1 \delta_i = -1 δi=−1,那么赌徒的资产将变为 R 1 = i − 1 R_1=i-1 R1=i−1,此时赌徒赢得赌博游戏的概率则变为 P i − 1 P_{i-1} Pi−1。这两种情况的概率分别为 p p p 和 1 − p 1-p 1−p,所以我们可以写为
P i = p P i + 1 + ( 1 − p ) P i − 1 P_i=pP_{i+1}+(1-p)P_{i-1} Pi=pPi+1+(1−p)Pi−1
对上式进行变换得到
p P i + ( 1 − p ) P i = p P i + 1 + ( 1 − p ) P i − 1 pP_i+(1-p)P_i=pP_{i+1}+(1-p)P_{i-1} pPi+(1−p)Pi=pPi+1+(1−p)Pi−1
即
P i + 1 − P i = 1 − p p ( P i − P i − 1 ) P_{i+1}-P_i=\frac{1-p}{p}(P_i-P_{i-1}) Pi+1−Pi=p1−p(Pi−Pi−1)
因为 P 2 − P 1 = 1 − p p ( P 1 − P 0 ) = 1 − p p P 1 P_2-P_1=\frac{1-p}{p}(P_1-P_0)=\frac{1-p}{p}P_1 P2−P1=p1−p(P1−P0)=p1−pP1,所以我们可以通过递推得到
P i + 1 − P i = ( 1 − p p ) i P 1 P_{i+1}-P_i=(\frac{1-p}{p})^iP_1 Pi+1−Pi=(p1−p)iP1
由等比级数的性质最终可以得到
P i + 1 = ∑ k = 0 i ( 1 − p p ) k P 1 P_{i+1}=\sum_{k=0}^{i}(\frac{1-p}{p})^kP_1 Pi+1=k=0∑i(p1−p)kP1
令 i = N − 1 i=N-1 i=N−1,根据 P N = 1 P_N=1 PN=1 的性质可以得到
1 = P N = P 1 1 − ( 1 − p p ) N 1 − 1 − p p , p ≠ 0.5 1=P_N= \ P_{1}\frac{1-(\frac{1-p}{p})^{N}}{1-\frac{1-p}{p}}, \ p \neq 0.5 1=PN= P11−p1−p1−(p1−p)N, p=0.5
1 = P N = P 1 N , p = 0.5 \ 1=P_N=P_1N, \ p = 0.5 1=PN=P1N, p=0.5
最终我们可以得到赌徒以初始资产 i i i 赢得 N N N 元的概率为
P i = 1 − ( 1 − p p ) i 1 − ( 1 − p p ) N , p ≠ 0.5 P_i= \ \frac{1-(\frac{1-p}{p})^{i}}{1-(\frac{1-p}{p})^N}, \ p \neq 0.5 Pi= 1−(p1−p)N1−(p1−p)i, p=0.5
P i = i N , p = 0.5 \ P_i=\frac{i}{N}, \ p = 0.5 Pi=Ni, p=0.5
当 N N N 趋向于无穷大时,若 p > 0.5 p > 0.5 p>0.5
lim N → inf P i = 1 − ( 1 − p p ) i > 0 \lim_{N\rightarrow \inf} P_i=1-(\frac{1-p}{p})^i>0 N→inflimPi=1−(p1−p)i>0
若 p ≤ 0.5 p\leq0.5 p≤0.5
lim N → inf P i = 0 \lim_{N\rightarrow \inf} P_i=0 N→inflimPi=0
举例:
A同学有1元钱,参与一场赌博赢的概率为0.6,那么A同学破产之前资产达到4元的概率是多少?
根据之前推导的公式,我们可以得到 P 1 = 27 65 = 0.415 P_1=\frac{27}{65}=0.415 P1=6527=0.415
拜占庭将军问题 Byzantine Generals’ Problem
(以后补充)
参考
Nash Equilibrium https://www.investopedia.com/terms/n/nash-equilibrium.asp
What is Nash Equilibrium? https://corporatefinanceinstitute.com/resources/knowledge/economics/nash-equilibrium-game-theory/
Pareto Efficiency https://www.investopedia.com/terms/p/pareto-efficiency.asp
What is Pareto Efficiency?https://corporatefinanceinstitute.com/resources/knowledge/economics/pareto-efficiency/
Gambler’s Ruin Problemhttp://www.columbia.edu/~ks20/FE-Notes/4700-07-Notes-GR.pdf
te.com/resources/knowledge/economics/pareto-efficiency/>
Gambler’s Ruin Problemhttp://www.columbia.edu/~ks20/FE-Notes/4700-07-Notes-GR.pdf