零知识证明 - bellman源码分析

bellman是Zcash团队用Rust语言开发的一个zk-SNARK软件库，实现了Groth16算法。
项目地址：https://github.com/zcash/librustzcash/tree/master/bellman

1. 总体流程

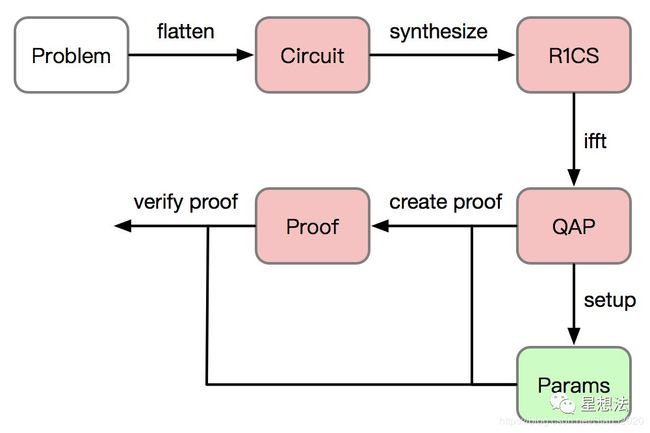
总体流程大致可以分为以下几个步骤：
1.将问题多项式拍平（flatten），构建对应的电路（Circuit）。这一步是由上层应用程序配置的。
2.根据电路生成R1CS（Rank 1 Constraint System）
3.将R1CS转化为QAP（Quadratic Arithmetic Program）。传统做法是通过拉格朗日插值，但是为了降低计算复杂度，可以通过快速傅立叶变换来实现。
4.初始化QAP问题的参数，即CRS（Common Reference Strings）
5.根据CRS和输入创建proof
6.验证proof

下面依次介绍各个步骤的细节。

2. Setup阶段：

Setup阶段最主要的工作是生成CRS数据，相关公式：
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ykwhzTEF-1594742340878)(零知识证明|bellman源码分析.resources/54C36D90-F201-4370-A78D-565031AAFFD9.png)]
注1：公式中的x对应代码中的变量tau，相应的$x^i$对应于powers_of_tau。
注2：$t(\tau )=(\tau -{\omega }^0)(\tau -{\omega }^1)...(\tau -{\omega }^{n-1})={\tau }^n-1$ ，代码中的powers_of_tau.z(&tau)就是计算该值。

2.1 参数数据结构

pub struct VerifyingKey {
    pub alpha_g1: E::G1Affine,
    pub beta_g1: E::G1Affine,
    pub beta_g2: E::G2Affine,
    pub gamma_g2: E::G2Affine,
    pub delta_g1: E::G1Affine,
    pub delta_g2: E::G2Affine,
    pub ic: Vec
}

其中$ic=\frac{\beta u_i(\tau )+\alpha v_i(\tau )+w_i(\tau )}{\gamma }$

pub struct Parameters {
    pub vk: VerifyingKey,
    pub h: Arc>,
    pub l: Arc>,
    pub a: Arc>,
    pub b_g1: Arc>,
    pub b_g2: Arc>
}

其中$h=\frac{{\tau }^{i}t(\tau )}{\delta }$，$l=\frac{\beta u_i(\tau )+\alpha v_i(\tau )+w_i(\tau )}{\delta }$
最后3个参数a, b_g1, b_g2似乎公式中没有出现，实际上它们是根据$x^i$算出来的QAP多项式的值，也就是$[u(x){]}_1,[v(x){]}_1,[v(x){]}_2$，后面在计算proof的时候会用到。以a为例，假设其中一个多项式的系数等于$c_0,c_1,...,c_{n-1}$，则$a={\Sigma }_{i=0}^{n-1}{c}_i{x}^i$，最后再映射到椭圆曲线上。

2.2 变量类型

Variable类型代表输入数据中的每一个值，分为公开的statement数据和私有的witness数据：

• Input类型：即statement数据
• Aux类型：即witness数据

pub enum Index {
    Input(usize),
    Aux(usize)
}
pub struct Variable(Index);

2.3 ConstraintSystem

ConstraintSystem是一个接口，定义了下面几个函数用于产生不同类型的变量：

• one(): 产生Input类型的变量，索引为0
• alloc(): 产生Aux类型的变量，索引递增
• alloc_input(): 产生Input类型的变量，索引递增

示例：

let a = cs.alloc(...)
let b = cs.alloc(...)
let c = cs.alloc_input(...)
cs.enforce(
    || "a*b=c",
    |lc| lc + a,
    |lc| lc + b,
    |lc| lc + c
);

在上面这个例子里，c是statement，a和b是witness，需要验证a * b = c这个Circuit。
如果想验证a + b = c，需要写成下面这样：

cs.enforce(
    || "a+b=c",
    |lc| lc + a + b,
    |lc| lc + CS::one(),
    |lc| lc + c
);

2.4 构建R1CS

Circuit的synthesize()会调用ConstraintSystem的enforce()构建R1CS。
KeypairAssembly是ConstraintSystem的一个实现，R1CS的参数会保存在其成员变量中：

struct KeypairAssembly {
    num_inputs: usize,
    num_aux: usize,
    num_constraints: usize,
    at_inputs: Vec>,
    bt_inputs: Vec>,
    ct_inputs: Vec>,
    at_aux: Vec>,
    bt_aux: Vec>,
    ct_aux: Vec>
}

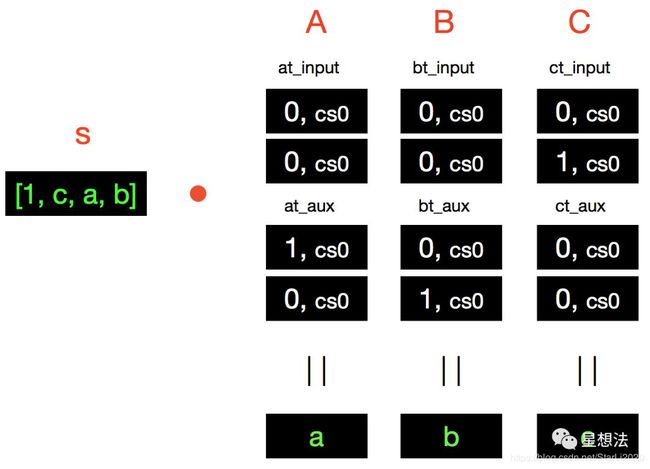
以上面的a * b = c为例：
num_inputs = 1
num_aux = 2
num_constraints = 1
后面6个字段就对应R1CS中的A、B、C矩阵：

2.5 构建QAP

接下来就是要完成R1CS到QAP的转换。其中有一步会利用逆离散快速傅立叶变换实现拉格朗日插值：

powers_of_tau.ifft(&worker);
let powers_of_tau = powers_of_tau.into_coeffs();

这里有一个单位根(root of unity)的概念：
如果${\omega }^n=1$，则称$\omega$为单位根。以复平面为例，${\omega }^i$实际上把单位圆等分成了n份。

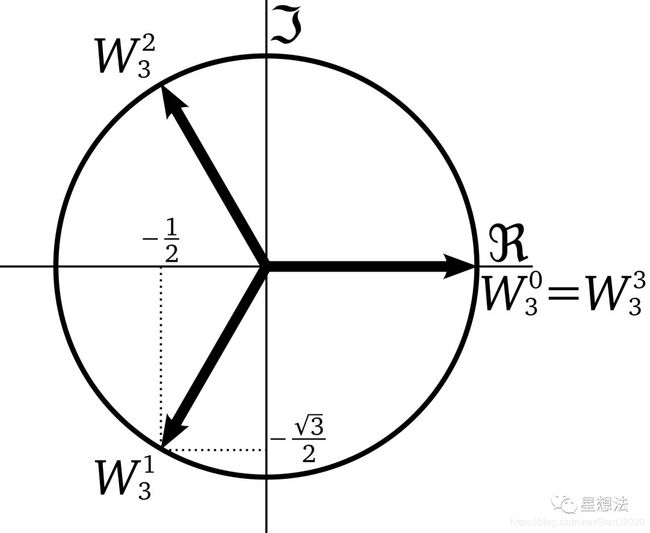
现在我们是在有限循环群的条件下，根据费马小定理：假如p是质数，且$\omega$和p互质，那么${\omega }^{p-1}(modp)=1$。因此，和p互质的素数都可以作为单位根。
同时我们发现，任何一个元素都可以用${\omega }^1,{\omega }^2,...,{\omega }^{p-1}$的线性组合来表示，也就是说它们可以作为循环群的一组基。我们利用这组基进行逆离散傅立叶变换，就可以得到拉格朗日插值系数，将R1CS转化为QAP。

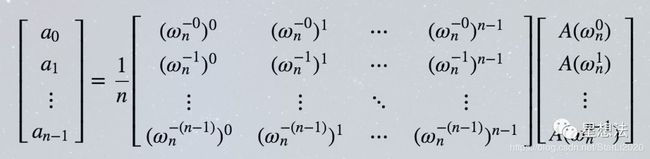
2.6 准备验证参数

最后，由于验证proof的时候需要用到下面公式里带中括号的那些参数：
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-80Kqu7Kh-1594742340883)(零知识证明|bellman源码分析.resources/1987F236-735B-4F40-BE7B-09C43AF40C5F.png)]
为了能快速验证，预先把这些参数的值计算出来。代码如下：

pub fn prepare_verifying_key(
    vk: &VerifyingKey
) -> PreparedVerifyingKey
{
    let mut gamma = vk.gamma_g2;
    gamma.negate();
    let mut delta = vk.delta_g2;
    delta.negate();

    PreparedVerifyingKey {
        alpha_g1_beta_g2: E::pairing(vk.alpha_g1, vk.beta_g2),
        neg_gamma_g2: gamma.prepare(),
        neg_delta_g2: delta.prepare(),
        ic: vk.ic.clone()
    }
}

一个小细节：在有限域中如何计算除法？
显然，$a÷b=a\times b^{-1}$，那么乘性逆元素（multiplicative inverse）$b^{-1}$如何计算呢？
根据费马小定理：假如p是质数，且a和p互质，那么$a^{p-1}(modp)=1$。
因此，在有限域中，$b^{-1}=b^{p-2}$。
对应代码：

fn inverse(&self) -> Option {
    if ::is_zero(self) {
        None
    } else {
        Some(self.pow(&[(MODULUS_R.0 as u64) - 2]))
    }
}

3. 创建Proof阶段

Groth16算法生成Proof的公式如下：
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-N8WtAX9v-1594742340885)(零知识证明|bellman源码分析.resources/96969F8D-9104-4322-B60E-F417869ABE72.png)]
随机选取r和s，计算$[A{]}_1,[B{]}_2,[C{]}_1$这三个值。

pub struct Proof {
    pub a: E::G1Affine,
    pub b: E::G2Affine,
    pub c: E::G1Affine
}

公式中其他的参数都是已知的，最主要的难点是计算h(x)，下面会进行详细介绍。

3.1 计算$s\cdot A(x),s\cdot B(x),s\cdot C(x)$

回顾一下QAP，我们需要通过拉格朗日插值，把R1CS转化为一系列多项式：
$A(x)=[A_0(x),A_1(x),...,A_m(x)]$
$B(x)=[B_0(x),B_1(x),...,B_m(x)]$
$C(x)=[C_0(x),C_1(x),...,C_m(x)]$
然后我们需要验证$s\cdot A(x)\ast s\cdot B(x)-s\cdot C(x)=h(x)\ast t(x)$。
因此，我们需要计算$s\cdot A(x),s\cdot B(x),s\cdot C(x)$。一种方法是直接进行多项式运算，还有一种方法是算出它们在${\omega }^0,{\omega }^1,{\omega }^2,...,{\omega }^{n-1}$处的值，然后通过iFFT（逆快速傅立叶变换）获得多项式系数。
值得注意的是，当x分别取${\omega }^0,{\omega }^1,{\omega }^2,...,{\omega }^{n-1}$时，$A(x),B(x),C(x)$的值其实就是R1CS的值。因此，$s\cdot A(x)$其实就是所有门电路的左输入，$s\cdot B(x)$就是所有门电路的右输入，而$s\cdot C(x)$就是所有门电路的输出。我们可以复用Circuit的synthesize()函数来进行计算。
生成proof的时候使用的是ConstraintSystem的另外一个实现ProvingAssignment来调用Circuit的synthesize()函数。

struct ProvingAssignment {
    ...
    a: Vec>,
    b: Vec>,
    c: Vec>,

    input_assignment: Vec,
    aux_assignment: Vec
}

和Setup阶段基本类似：

• alloc()：把witness数据送入aux_assignment中
• alloc_input()：把statement数据送入input_assignment中
• enforce()/eval()：计算出$s\cdot A(x),s\cdot B(x),s\cdot C(x)$，分别放入a、b、c这3个成员变量中

然后就可以通过iFFT获得对应的多项式系数了。

3.2 计算h(x)

有了$s\cdot A(x),s\cdot B(x),s\cdot C(x)$，就可以计算h(x)了：
$h(x)=\frac{s\cdot A(x)\ast s\cdot B(x)-s\cdot C(x)}{t(x)}$
但是这里有个问题，$t(x)=(x-{\omega }^0)(x-{\omega }^1)...(x-{\omega }^{n-1})=x^n-1$，而x的取值是${\omega }^0,{\omega }^1,{\omega }^2,...,{\omega }^{n-1}$，所以分母为零！显然我们是不能除以零的，因此需要对x做一定的“变换”或者“偏移”。用bellman里的术语，叫做从“Evaluation Domain”转换到“Coset”上。
1.定义$\omega ={\sigma }^{(r-1)/n}$，则${\omega }^n=1$（费马小定理）
2.先通过3次iFFT，计算出a，b，c的多项式系数
3.计算多项式在$\sigma {\omega }^0,\sigma {\omega }^1,...,\sigma {\omega }^{n-1}$这个“偏移集合”上的值
4.再通过3次FFT，获得偏移后的点的集合a’，b’，c’
5.由于$t(\sigma {\omega }^i)=(\sigma {\omega }^i{)}^n-1={\sigma }^n-1$，计算h(x)在偏移集合上的点$h(\sigma {\omega }^i)=\frac{a_i^{\prime }\ast b_i^{\prime }-c_i^{\prime }}{{\sigma }^n-1}$
6.做一次iFFT，计算出偏移后的多项式系数
7.根据尺度变换定理：$f(\sigma x)\leftarrow \to F(\frac{1}{\sigma }\omega )$，把上一步得到的结果除以$\sigma$，就获得了h(x)的多项式系数
根据以上分析，一共需要执行3次FFT，4次iFFT。
bellman基本上就是按照上面的算法来计算的，我们来详细分析一下。

首先，获取上一节的计算结果：

    let mut a = EvaluationDomain::from_coeffs(prover.a)?;
    let mut b = EvaluationDomain::from_coeffs(prover.b)?;
    let mut c = EvaluationDomain::from_coeffs(prover.c)?;

然后，通过3次iFFT获取多项式系数，计算在coset上的值，再通过3次FFT获取偏移后的点：

    a.ifft(&worker);
    a.coset_fft(&worker);
    b.ifft(&worker);
    b.coset_fft(&worker);
    c.ifft(&worker);
    c.coset_fft(&worker);

接下来，计算$h(\sigma {\omega }^i)=\frac{a_i^{\prime }\ast b_i^{\prime }-c_i^{\prime }}{{\sigma }^n-1}$：

    a.mul_assign(&worker, &b);
    drop(b);
    a.sub_assign(&worker, &c);
    drop(c);
    a.divide_by_z_on_coset(&worker);

最后，通过iFFT获取多项式系数，然后除以$\sigma$：

    a.icoset_fft(&worker);

另外，后面还有一步是计算$\frac{h(\tau )t(\tau )}{\delta }$，作为$[C{]}_1$的一部分：

    multiexp(&worker, params.get_h(a.len())?, FullDensity, a)

4. 验证阶段

Groth16算法的proof验证公式如下：
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-z3xOyIJO-1594742340886)(零知识证明|bellman源码分析.resources/94E9FC17-7AA8-4022-BAFB-DC00DA7A70F7.png)]
中间的求和部分参见以下代码（使用了CRS中的ic），生成中间变量acc：

    let mut acc = pvk.ic[0].into_projective();

    for (i, b) in public_inputs.iter().zip(pvk.ic.iter().skip(1)) {
        acc.add_assign(&b.mul(i.into_repr()));
    }

然后把公式略做变形，将问题转化为验证以下等式：
$[A{]}_1\cdot [B{]}_2+acc\cdot (-[\gamma {]}_2)+[C{]}_1\ast (-[delta{]}_2)=[\alpha {]}_1\cdot [\beta {]}_2$
对应代码如下：

    Ok(E::final_exponentiation(
        &E::miller_loop([
            (&proof.a.prepare(), &proof.b.prepare()),
            (&acc.into_affine().prepare(), &pvk.neg_gamma_g2),
            (&proof.c.prepare(), &pvk.neg_delta_g2)
        ].into_iter())
    ).unwrap() == pvk.alpha_g1_beta_g2)

至此，bellman源码的基本流程就分析完毕了，欢迎一起交流讨论～