Mahalanobis Distance和Euclidean Distance
马氏距离是一种有效的多元距离度量标准,用于测量点(向量)与分布之间的距离。常用在多变量异常检测,高度不平衡的数据集分类应用中。
本文解释为什么和何时用Mahalanobis Distance。
Euclidean Distance
欧几里德距离是两点之间常用的直线距离。
如果两个点都在二维平面中(也就是说,数据集中有两个数字列(![]() )和(
)和(![]() )),则两个点(
)),则两个点(![]() ,
,![]() )和(
)和(![]() ,
,![]() )之间的欧式距离 )是:
)之间的欧式距离 )是:
![]()
该公式可以扩展到所需的任意多个维度:
![]()
当数据点可均等加权且彼此独立,欧几里得距离就可以正常工作。
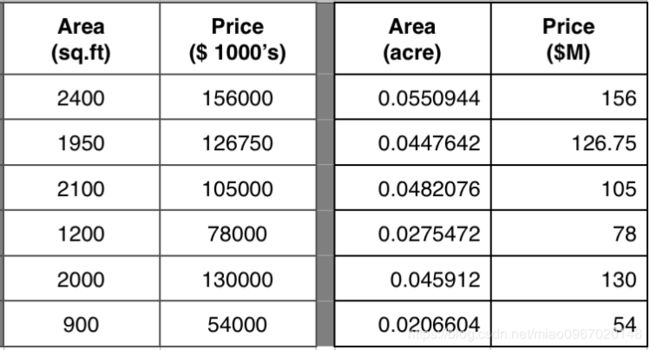
让我们考虑一个例子,如下表:
上面的两个表格显示了相同对象的“面积”和“价格”。 仅变量的单位改变。
由于两个表都表示相同的实体,因此任意两行(点A和点B)之间的距离都应该相同。 但是,即使在物理空间上,距离是相同的,欧几里得距离也给出了不同的值。
从技术上讲,可以通过缩放变量,计算z分数(例如:(x –平均值)/ std)或使其在特定范围内(例如:归一化)变化来克服。
但是还有另一个主要缺点。
也就是说,如果维度(数据集中的列)相互关联(这在实际数据集中通常是这种情况),则对于测量一点实际上离集群有多近,点与点中心(分布)之间的欧几里得距离所给出的信息很少或具有误导性。
如果![]() 和
和![]() 是不相关的,与中心点的欧几里得距离,可以用于辨别是否是内部成员。
是不相关的,与中心点的欧几里得距离,可以用于辨别是否是内部成员。
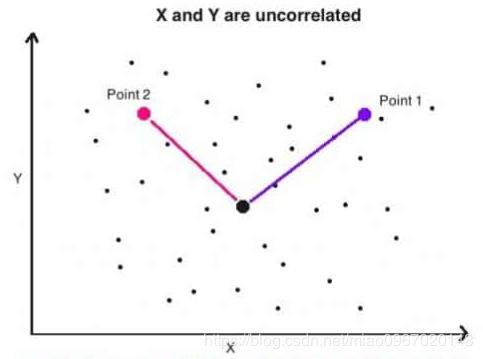
如果![]() 和
和![]() 是不相关的。Point 1和点2与中心点的欧几里得距离相同,但是Point 1属于分布,Point 2是离群点。为了检测Point 2是离群点,Point 1与中心点的距离应该大于Point 2 与中心点的距离。
是不相关的。Point 1和点2与中心点的欧几里得距离相同,但是Point 1属于分布,Point 2是离群点。为了检测Point 2是离群点,Point 1与中心点的距离应该大于Point 2 与中心点的距离。
这是因为,欧几里得距离仅是两点之间的距离。 它不考虑数据集中的其余点如何变化。 因此,它不能真正用来判断一个点实际上与点的分布有多接近。
这里我们需要的是更健壮的距离度量标准,该度量标准可以精确表示一个点距分布的距离。
Mahalanobis Distance
马氏距离是点与分布之间的距离。 并且不在两个不同的点之间。 它实际上是欧几里得距离的多元等效项。
它是由P. C. Mahalanobis教授于1936年提出的,此后一直在各种统计应用中使用。 但是,它在机器学习实践中并不为人所知或使用。
那么从计算上来说,马氏距离与欧几里得距离有何不同?
- Mahalanobis Distance将列转换为不相关的变量
- 缩放列以使其方差等于1
- 最后,Mahalanobis Distance计算出欧几里得距离
计算马氏距离的公式如下:
![]()
 是马氏距离的平方;
是马氏距离的平方; 是观测值的向量(数据集中的行);
是观测值的向量(数据集中的行); 是自变量平均值的向量(每列的平均值);
是自变量平均值的向量(每列的平均值);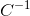 是自变量的逆协方差矩阵。
是自变量的逆协方差矩阵。
![]() 本质上是向量与平均值的距离。 然后,将其除以协方差矩阵(或乘以协方差矩阵的逆数)。
本质上是向量与平均值的距离。 然后,将其除以协方差矩阵(或乘以协方差矩阵的逆数)。
考虑一下,这实际上是常规标准化的多元变量(![]() )。 也就是说,
)。 也就是说,![]() =(
=(![]() 向量)–(平均向量)/(协方差矩阵)。
向量)–(平均向量)/(协方差矩阵)。
那么,除以协方差的作用是什么?
如果数据集中的变量高度相关,则协方差将很高。 除以较大的协方差将有效地减小距离。
同样,如果X不相关,则协方差也不大,距离也不会减少太多。
因此,Mahalanobis Distance有效地解决了规模问题以及谈到的变量之间的相关性。
Mahalanobis Distance in Python
import pandas as pd
import scipy as sp
import numpy as np
filepath = 'https://raw.githubusercontent.com/selva86/datasets/master/diamonds.csv'
df = pd.read_csv(filepath).iloc[:, [0,4,6]]
print(df.head())def mahalanobis(x=None, data=None, cov=None):
"""Compute the Mahalanobis Distance between each row of x and the data
x : vector or matrix of data with, say, p columns.
data : ndarray of the distribution from which Mahalanobis distance of each observation of x is to be computed.
cov : covariance matrix (p x p) of the distribution. If None, will be computed from data.
"""
x_minus_mu = x - np.mean(data)
if not cov:
cov = np.cov(data.values.T)
inv_covmat = np.linalg.inv(cov)
left_term = np.dot(x_minus_mu, inv_covmat)
mahal = np.dot(left_term, x_minus_mu.T)
return mahal.diagonal()
df_x = df[['carat', 'depth', 'price']].head(500)
df_x['mahala'] = mahalanobis(x=df_x, data=df[['carat', 'depth', 'price']])
print(df_x.head())使用马氏距离的多元离群值检测
假设检验统计量遵循卡方分布,自由度为“ ![]() ”,则在0.01显着性水平和2自由度下的临界值计算如下:
”,则在0.01显着性水平和2自由度下的临界值计算如下:
# Critical values for two degrees of freedom
from scipy.stats import chi2
chi2.ppf((1-0.01), df=2)
#> 9.21这意味着,如果观测值的马氏距离超过9.21,则可以认为是极端。
如果更喜欢P值来确定观察值是否为极值,则可以按以下方式计算P值:
# Compute the P-Values
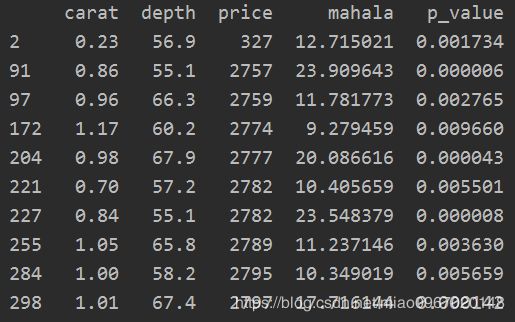
df_x['p_value'] = 1 - chi2.cdf(df_x['mahala'], 2)
# Extreme values with a significance level of 0.01
print(df_x.loc[df_x.p_value < 0.01].head(10))如果将上述观察值与数据集的其余部分进行比较,则显然是极端的。
Mahalanobis Distance for Classification Problems
马氏距离可用于分类问题。 Mahalanobis分类器简单实现在下面编码。 直觉是,根据马哈拉诺比斯距离,将观察值分配给与其最接近的类别。
看一下BreastCancer数据集上实现的示例,其目的是确定肿瘤是良性还是恶性的。
df = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/BreastCancer.csv',
usecols=['Cl.thickness', 'Cell.size', 'Marg.adhesion',
'Epith.c.size', 'Bare.nuclei', 'Bl.cromatin', 'Normal.nucleoli',
'Mitoses', 'Class'])
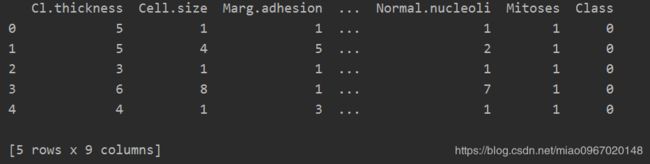
df.dropna(inplace=True) # drop missing values.
print(df.head())以7:3的比例将数据集拆分为训练和测试。 然后将训练数据集分为“ pos”(1)和“ neg”(0)类的同类组。 为了预测测试数据集的类别,我们测量给定观测值(行)与正值数据集(xtrain_pos)和负值数据集(xtrain_neg)之间的马氏距离。
然后,根据观察到的最接近的组为其分配类别。
from sklearn.model_selection import train_test_split
xtrain, xtest, ytrain, ytest = train_test_split(df.drop('Class', axis=1), df['Class'], test_size=.3, random_state=100)
# Split the training data as pos and neg
xtrain_pos = xtrain.loc[ytrain == 1, :]
xtrain_neg = xtrain.loc[ytrain == 0, :]构建MahalanobiBinaryClassifier。 为此,需要定义predict_proba()和predict()方法。 此分类器不需要单独的fit()(训练)方法。
class MahalanobisBinaryClassifier():
def __init__(self, xtrain, ytrain):
self.xtrain_pos = xtrain.loc[ytrain == 1, :]
self.xtrain_neg = xtrain.loc[ytrain == 0, :]
def predict_proba(self, xtest):
pos_neg_dists = [(p,n) for p, n in zip(mahalanobis(xtest, self.xtrain_pos), mahalanobis(xtest, self.xtrain_neg))]
return np.array([(1-n/(p+n), 1-p/(p+n)) for p,n in pos_neg_dists])
def predict(self, xtest):
return np.array([np.argmax(row) for row in self.predict_proba(xtest)])
clf = MahalanobisBinaryClassifier(xtrain, ytrain)
pred_probs = clf.predict_proba(xtest)
pred_class = clf.predict(xtest)
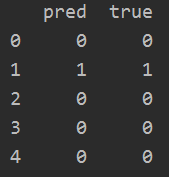
# Pred and Truth
pred_actuals = pd.DataFrame([(pred, act) for pred, act in zip(pred_class, ytest)], columns=['pred', 'true'])
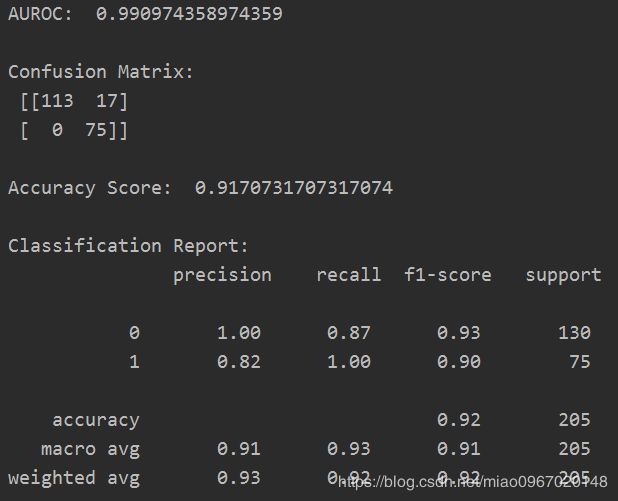
print(pred_actuals[:5]) 分类器如何在测试数据集上执行
from sklearn.metrics import classification_report, accuracy_score, roc_auc_score, confusion_matrix
truth = pred_actuals.loc[:, 'true']
pred = pred_actuals.loc[:, 'pred']
scores = np.array(pred_probs)[:, 1]
print('AUROC: ', roc_auc_score(truth, scores))
print('\nConfusion Matrix: \n', confusion_matrix(truth, pred))
print('\nAccuracy Score: ', accuracy_score(truth, pred))
print('\nClassification Report: \n', classification_report(truth, pred))