Proof Systems for General Statements about Discrete Logarithms 学习笔记

Jan Camenisch和Markus Stadler 1997年论文《Proof Systems for General Statements about Discrete Logarithms》。

1. 背景知识

• Monotone Boolean function定义：
  
  

• Concatenation of tuples：
  

• Modified Cartesian Product：
  

• Knowledge specification set：
  
  

2. 一些例子

2.1 Prove knowledge of discrete logarithm $y=g^x$ (Schnorr signature for message $(g,y)$)

博客 基于Sigma protocol实现的零知识证明protocol集锦 中1.2节类似：
Witness：$x$
Instance：$y$和$g$
Relation：$y=g^x$

具体实现思路为：

• 1）Prover：Prover生成随机数$v{\in }_R{\mathbb{Z}}_q$，创建commitment $t=g^v$；Prover将$g,t,y$作为hash函数输入计算challenge $c(=Hash(g,y,t))$；Prover计算response $r=v-c\ast x(\mathrm{m}\mathrm{o}\mathrm{d}q)$。Prover将$(c,r)$发送给Verifier。

Verifier根据收到的$(c,r)$，假设$g^r=y^{-c}\ast t^{\prime }$成立，计算$t^{\prime }(=g^r\ast y^c)$，利用$g,y,t^{\prime }$作为相同hash函数的输入，计算$c^{\prime }=hash(g,y,t^{\prime })$，验证$c=c^{\prime }$是否成立即可。

2.2 Prove knowledge of two discrete logarithms satisfy a linear equation

Witness：$x_1,x_2$
Instance：$g_1,y_1,g_2,y_2,a_1,a_2,b$
Relation：$y_1=g^{x_1}\Lambda y_2=g^{x_2}\Lambda a_1{x}_1+a_2{x}_2=b(\mathrm{m}\mathrm{o}\mathrm{d}q)$
用knowledge specification set表示的Relation为：$K=(DL(g_1,y_1)\otimes DL(g_2,y_2))\cap LE((a_1,a_2),b)$

具体实现为：

• 1）Prover：Prover生成满足$a_1{v}_1+a_2{v}_2=0(\mathrm{m}\mathrm{o}\mathrm{d}q)$的随机数$v_1和v_2$【数学描述为$(v_1,v_2){\in }_R\{(u_1,u_2)\in {\mathbb{Z}}_q|a_1{u}_1+a_2{u}_2=0(\mathrm{m}\mathrm{o}\mathrm{d}q)\}$】，创建commitment $t_1=g_1^{v_1},t_2=g_2^{v_2}$；Prover将$g_1,y_1,g_2,y_2,a_1,a_2,b,t_1,t_2$作为hash函数输入计算challenge $c(=Hash(g_1,y_1,g_2,y_2,a_1,a_2,b,t_1,t_2))$；Prover计算response $r_1=v_1-c\ast x_1(\mathrm{m}\mathrm{o}\mathrm{d}q),r_2=v_2-c\ast x_2(\mathrm{m}\mathrm{o}\mathrm{d}q)$。Prover将$(c,r_1,r_2)$发送给Verifier。

Verifier根据收到的$(c,r_1,r_2)$，假设$g^r=y^{-c}\ast t^{\prime }$成立，计算$t_1^{\prime }(=g_1^{r_1}\ast y_1^c),t_2^{\prime }(=g_2^{r_2}\ast y_2^c)$，利用$g_1,y_1,g_2,y_2,a_1,a_2,b,t_1^{\prime },t_2^{\prime }$作为相同hash函数的输入，计算$c^{\prime }=hash(g_1,y_1,g_2,y_2,a_1,a_2,b,t_1^{\prime },t_2^{\prime })(\mathrm{m}\mathrm{o}\mathrm{d}q)$，验证$c=c^{\prime }$是否成立以及$a_1{r}_2+a_2{r}_2=-cb(\mathrm{m}\mathrm{o}\mathrm{d}q)$是否成立即可。

2.3 OR proof

博客 基于Sigma protocol实现的零知识证明protocol集锦 中2.3节类似：
Witness：$x_1$ OR $x_2$
Instance：$g_1,y_1,g_2,y_2$
Relation：$y_1=g_1^{x_1}$ OR $y_2=g_2^{x_2}$

假设Prover知道$x_1$（<1>），而不知道$x_2$（<2>）。
详细实现为：
1）Prover：

• 生成用于证明<1>随机数$v_1$，构建第1个commitment $t_1=g_1^{v_1}$；
• 生成用于证明<2>的challenge $c_2$和随机response $r_2$，（由于Prover由于不知道$b$，只能随机生成，采用 博客 基于Sigma protocol实现的零知识证明protocol集锦 1.2.2节中的方式来伪造证明）计算$t_2=y_2^{c_2}\ast g^{r_2}$；
• 计算hash值$c=Hash(g_1,y_1,g_2,y_2,t_1,t_2)$，计算用于证明<1>的challenge $c_1=c-c_2$；
• 计算用于证明<1>的response $r_1=v_1-c_1\ast x_1$；
• 发送$((c_1,r_1),(c_2,r_2))$ 给Verifier。

2）Verifier：
根据收到的proof $((c_1,r_1),(c_2,r_2))$，计算$t_1^{\prime }=g_1^{r_1}{y}_1^{c_1},t_2^{\prime }=g_2^{r_2}{y}_2^{c_2}$，同时验证$c_1+c_2=H(g_1,y_1,g_2,y_2,t_1^{\prime },t_2^{\prime })(\mathrm{m}\mathrm{o}\mathrm{d}q)$是否成立即可。

The reason why this works is that the prover is “allowed to forge” one of the two proofs since he can choose the corresponding challenge before the commitment is computed; the other challenge is then determined by the hash function. The verifier, however, cannot decide which challenge was chosen and therefore obtains no information about which discrete loarithms the prover knows.

3 prove knowledge of an element of an arbitrary knowledge specification set

即构建an element of an aribitrary knowledge specification set。 OR证明的generalization。

3.1 Transformation and Tree-Representation：

3.2 Constructing a proof for $F$

$F$为knowledge specification，可表示为$\tilde{F}={\bigcup }_{i=1}^m{\tilde{F}}_i$，其中${\tilde{F}}_i$中没有任何形式的$\cup$操作。
假设Prover知道an element $K\in F$，则意味着存在an index $\alpha \in {\tilde{F}}_{\alpha }$。$K$为a tuple of elements of ${\mathbb{Z}}_q$。

证明方式如下：
1）Commitment：
（a）设置${\bar{w}}_{\alpha }=0$，对于$i\ne \alpha$，则选择随机数${\bar{w}}_i{\in }_R{\mathbb{Z}}_q$。构建$\bar{W}=({\bar{w}}_1,\cdots ,{\bar{w}}_m)$。【${\bar{w}}_i$是对整个tree ${\tilde{F}}_i$全局的，当${\bar{w}}_i\ne 0$意味着是提前预测了challenge伪造了证明，仅对${\bar{w}}_i=0$的tree是知道witness的正确证明。】
（b）选择满足$E{|}_{W=\bar{W}}$的random tuple $\bar{V}=({\bar{v}}_{1.0\cdots ,1,\cdots },{\bar{v}}_{m.0\cdots ,.})$。
（c）为forest $\tilde{F}$的每一个node $n$配置commitment $T_n$：

• 若$n$为a leaf of type $DL(g,y)$ in the tree ${\tilde{F}}_i$，则：
  $T_n=(y^{{\bar{w}}_i}{g}^{{\bar{v}}_n})$
• 若$n$为 a leaf ot type $REP((g_1,\cdots ,g_k),y)$ in the tree ${\tilde{F}}_i$，则：
  $T_n=(y^{{\bar{w}}_i}{\prod }_{j=1}^k{g}_j^{{\bar{v}}_{n,j}})$
• 若$n$为a leaf of type $LE((a_1,\cdots ,a_k),b)$，则：
  $T_n$为empty tuple $()$
• 若$n$为$\otimes$或$\cap$的inner node，则：
  $T_n=T_{n||0}\circ T_{n||1}$

所有的Commitment $T$表示为：
$T=T_{1.0}\circ \cdots \circ T_{m.0}$

2）Challenge：
The challenge $C=(c_1,\cdots ,c_m)$，计算规则为：
$c_i=\{\begin{array}{cc}H(\tilde{F},T)-{\sum }_{j=1}^m{\bar{w}}_j(\mathrm{m}\mathrm{o}\mathrm{d}q)& \text{for }i=\alpha \\ {\bar{w}}_i& \text{otherwise}\end{array}$

3）Response：
Given $K\in {\tilde{F}}_{\alpha }$，the prover can construct a tuple $X$满足以下条件：（the components of $X$ are labeled in the same way as the components of $V$）

• $x_{n,j}=0$ for all indices $j$ if the leaf $n$ is $not$in the tree ${\tilde{F}}_{\alpha }$；
• 若$n$为a leaf of the type $DL$或者$REP$ in $F_{\alpha }$，则 sub-tuple $(x_{n,1},\cdots ,x_{n,k})$为 an element of the set defined by the type of the leaf。
• $X_{\alpha .0}$应使$E_{\alpha .0}{|}_{w_{\alpha }=-1}$成立，其中$X_{\alpha .0}$是对应sub-tuple $V_{\alpha .0}$的sub-tuple。

所有的response $R=(r_{1.0\cdots ,1,\cdots },r_{m.0\cdots ,.})$定义为：
$r_{n,j}={\bar{v}}_{n,j}-c_{\alpha }{x}_{n,j}(\mathrm{m}\mathrm{o}\mathrm{d}q)$
for all leaves $n$ and all indices $j$。

The proof of knowledge 为pair $(C,R)$。

3.3 Verifying a proof

The verification of a proof $(C,R)$ 主要分两步：
1）重构commitment：

• 若$n$为a leaf of type $DL(g,y)$ in the tree ${\tilde{F}}_i$，则：
  $T_n^{\prime }=(y^{c_i}{g}^{r_n})$
• 若$n$为a leaf ot type $REP((g_1,\cdots ,g_k),y)$ in the tree ${\tilde{F}}_i$，则：
  $T_n^{\prime }=(y^{c_i}{\prod }_{j=1}^k{g}_j^{r_{n,j}})$
• 若$n$为a leaf of type $LE((a_1,\cdots ,a_k),b)$，则：
  $T_n^{\prime }$为empty tuple $()$
• 若$n$为$\otimes$或$\cap$的inner node，则：
  $T_n^{\prime }=T_{n||0}^{\prime }\circ T_{n||1}^{\prime }$

2）Verifying the challenge and the response by：

• 验证$H(\tilde{F},T^{\prime })={\sum }_{i=1}^m{c}_i(\mathrm{m}\mathrm{o}\mathrm{d}q)$成立。
• 验证$R$使得$E{|}_{W=C}$成立。

3.4 举例

Witness：$x_1,x_2,x_3$
Instance：$h,z,g_1,g_2,y,a_1,a_2,a_3,b$
Relation：$(z=h^{x_1},y=g_1^{x_2}{g}_2^{x_3})$ 使得$b=a_1{x}_1+a_2{x}_2+a_3{x}_3(\mathrm{m}\mathrm{o}\mathrm{d}q)$成立 或 使得 $b=a_1{x}_2+a_2{x}_3+a_3{x}_1(\mathrm{m}\mathrm{o}\mathrm{d}q)$成立。
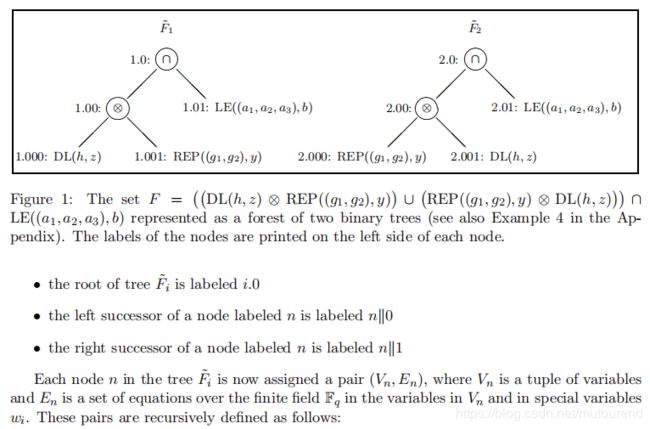
用knowledge specification set表示的Relation为：$F=((DL(h,z)\otimes REP((g_1,g_2),y))\cup (REP((g_1,g_2),y)\otimes DL(h,z)))\cap LE((a_1,a_2,a_3),b)$

进一步表示为：$\tilde{F}=((DL(h,z)\otimes REP((g_1,g_2),y))\cap LE((a_1,a_2,a_3),b)\cup (REP((g_1,g_2),y)\otimes DL(h,z))\cap LE((a_1,a_2,a_3),b)={\tilde{F}}_1\cup {\tilde{F}}_2$
可以具体表示为如下图示：

接下来，Prover需要构建the lists of variables $V_n$ 和 the set of equations $E_n$ for each node。
对tree ${\tilde{F}}_1$有：

• node $1.000$：$V_{1.000}=(v_{1.000,1})$
  $E_{1.000}=\varnothing$
• node $1.001$：$V_{1.001}=(v_{1.001,1},v_{1.001,2})$
  $E_{1.001}=\varnothing$
• node $1.00$：$V_{1.00}=V_{1.000}\circ V_{1.001}=(v_{1.000,1},v_{1.001,1},v_{1.001,2})$
  $E_{1.00}=E_{1.000}\cup E_{1.001}=\varnothing$
• node $1.01$：$V_{1.01}=(v_{1.01,1},v_{1.01,2},v_{1.01,3})$
  $E_{1.01}=\{a_1{v}_{1.01,1}+a_2{v}_{1.01,2}+a_3{v}_{1.01,3}=-w_{1}b\}$
• node $1.0$：$V_{1.0}=(v_{1.000,1},v_{1.001,1},v_{1.001,2},v_{1.01,1},v_{1.01,2},v_{1.01,3})$
  $E_{1.0}=\{v_{1.01,1}=v_{1.000,1},v_{1.01,2}=v_{1.001,1},v_{1.01,3}=v_{1.001,2},a_1{v}_{1.01,1}+a_2{v}_{1.01,2}+a_3{v}_{1.01,3}=-w_{1}b\}$

对tree ${\tilde{F}}_2$有：

• node $2.000$：$V_{2.000}=(v_{2.000,1},v_{2.000,2})$
  $E_{2.000}=\varnothing$
• node $2.001$：$V_{2.001}=(v_{2.001,1})$
  $E_{2.001}=\varnothing$
• node $2.00$：$V_{2.00}=V_{2.000}\circ V_{2.001}=(v_{2.000,1},v_{2.000,2},v_{2.001,1})$
  $E_{2.00}=E_{2.000}\cup E_{2.001}=\varnothing$
• node $2.01$：$V_{2.01}=(v_{2.01,1},v_{2.01,2},v_{2.01,3})$
  $E_{2.01}=\{a_1{v}_{2.01,1}+a_2{v}_{2.01,2}+a_3{v}_{2.01,3}=-w_{2}b\}$
• node $2.0$：$V_{2.0}=(v_{2.000,1},v_{2.000,2},v_{2.001,1},v_{2.01,1},v_{2.01,2},v_{2.01,3})$
  $E_{2.0}=\{v_{2.01,1}=v_{2.000,1},v_{2.01,2}=v_{2.000,2},v_{2.01,3}=v_{2.001,1},a_1{v}_{2.01,1}+a_2{v}_{2.01,2}+a_3{v}_{2.01,3}=-w_{2}b\}$

最后：
对$E_{1.0}$和$E_{2.0}$进行merge后，得到：
$E=\{v_{1.01,1}=v_{1.000,1},v_{1.01,2}=v_{1.001,1},v_{1.01,3}=v_{1.001,2},a_1{v}_{1.01,1}+a_2{v}_{1.01,2}+a_3{v}_{1.01,3}=-w_{1}b,v_{2.01,1}=v_{2.000,1},v_{2.01,2}=v_{2.000,2},v_{2.01,3}=v_{2.001,1},a_1{v}_{2.01,1}+a_2{v}_{2.01,2}+a_3{v}_{2.01,3}=-w_{2}b\}$
$V=V_{1.0}\circ V_{2.0}=(v_{1.000,1},v_{1.001,1},v_{1.001,2},v_{1.01,1},v_{1.01,2},v_{1.01,3},v_{2.000,1},v_{2.000,2},v_{2.001,1},v_{2.01,1},v_{2.01,2},v_{2.01,3})=({\bar{v}}_1,{\bar{v}}_2,{\bar{v}}_3,{\bar{v}}_1,{\bar{v}}_2,{\bar{v}}_3,{\bar{v}}_4,{\bar{v}}_5,{\bar{v}}_6,{\bar{v}}_4,{\bar{v}}_5,{\bar{v}}_6)$
$W=(w_1,w_2)$

1）Prover构建proof的方式可为：

• 随机选择$\bar{W}=({\bar{w}}_1,{\bar{w}}_2)=(0,w)，其中w{\in }_R{\mathbb{Z}}_q$；【即此时选择$\alpha =1$】
• 随机选择a random tuple $\bar{V}{\in }_R{\mathbb{Z}}_q^{12}$使得满足$E{|}_{W=\bar{W}}$成立即可。即随机选择${\bar{v}}_1,\cdots ,{\bar{v}}_6\in {\mathbb{Z}}_q$，使得$a_1{\bar{v}}_1+a_2{\bar{v}}_2+a_3{\bar{v}}_3=0(\mathrm{m}\mathrm{o}\mathrm{d}q)$和$a_1{\bar{v}}_4+a_2{\bar{v}}_5+a_3{\bar{v}}_6=-wb(\mathrm{m}\mathrm{o}\mathrm{d}q)$均成立。设置$V=({\bar{v}}_1,{\bar{v}}_2,{\bar{v}}_3,{\bar{v}}_1,{\bar{v}}_2,{\bar{v}}_3,{\bar{v}}_4,{\bar{v}}_5,{\bar{v}}_6,{\bar{v}}_4,{\bar{v}}_5,{\bar{v}}_6)$
• 构建commitment：$T=T_{1.0}\circ T_{2.0}=(h^{{\bar{v}}_1},g_1^{{\bar{v}}_2}{g}_2^{{\bar{v}}_3},z^w{h}^{{\bar{v}}_4},y^w{g}_1^{{\bar{v}}_5}{g}_2^{{\bar{v}}_6})$
  
• 计算challenge：$C=(c_1,c_2)=(H(\tilde{F},T)-w(\mathrm{m}\mathrm{o}\mathrm{d}q),w)$。
• 计算response：构建list $X=(x_1,x_2,x_3,x_1,x_2,x_3,0,0,0,0,0,0)$【针对此处$\alpha =1$】，计算response $R$中的$r_{i,j,l}$（所有方程式都是modulo $q$）：
  

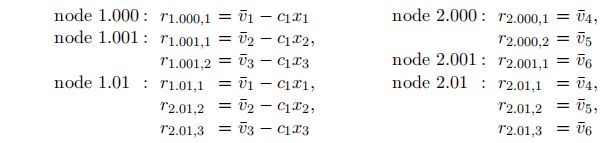
在整个proof内容即为$(C,R)$。

2）Verifier验证proof $(C,R)$ 的过程为：

• 重构commitment：$T^{\prime }=T_{1.0}^{\prime }\circ T_{2.0}^{\prime }$
  
• check challenge和equations of $E{|}_{W=C}$（均为modulo $q$运算）：
  

注意以上算法未做优化。

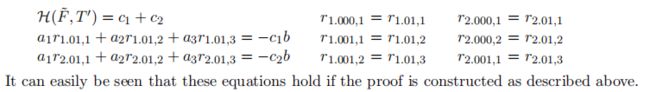
参考资料：
[1] Monotone Boolean function
[2] 博客 基于Sigma protocol实现的零知识证明protocol集锦