计算机视觉----图像底层特征提取之边缘提取（一）

图像底层特征提取是计算机视觉的基本步骤
1：边缘和轮廓能反映图像内容；
2：如果能对边缘和关键点可靠提取的话，很多视觉问题就基本上得到了解决

边缘的定义

• “边缘是图像中亮度突然变化的区域。”
• “图像灰度构成的曲面上的陡峭区域。”
• “像素灰度存在阶跃变化或屋脊状变化的像素的集合。”

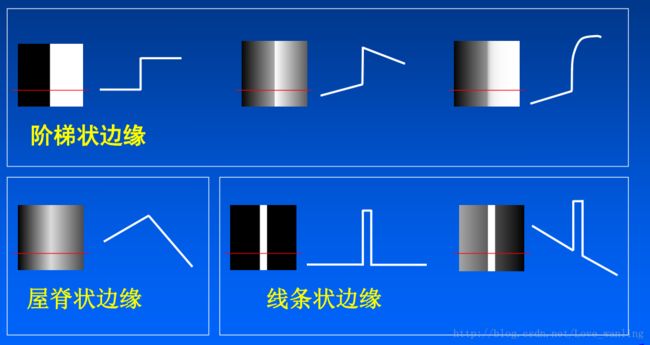
灰度图像中的边缘类型

边缘的提取

灰度图象边缘提取，主要的思想：
- 抑制噪声（低通滤波、平滑、去噪、模糊）
- 边缘特征增强（高通滤波、锐化）
- 边缘定位

图像微分算子

图像微分算子分为一阶微分算子和二阶微分算子。一阶微分算子最大值的，二阶微分算子过零点都是对应边缘。
考虑下面的图像：

它的数据表示如下：

对f(x)求导，得到一阶微分图像：

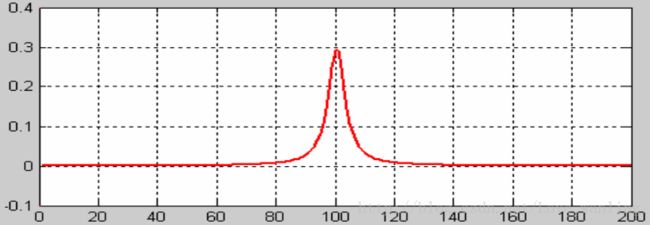
一阶微分在100处取得最大值，即此处的变化最大，为边缘。接下来我们看看二阶导数情况：

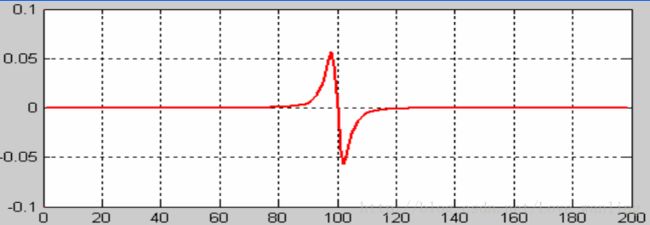
可以看出，二阶导数的过零点也是边界。但是要注意，过零点两侧要有符号变换，因为常数函数也是二阶导数为0。

在数字图像上计算梯度

根据导数的定义一阶导数可以写成：

f′(x)=dfdx=limΔx→0f(x+Δx)−f(x−Δx)2Δx

对于离散的数字信号，可以使用差分法近似：

f′(x)≈f(x+1)−f(x−1)2

相当于下面的卷积运算：

噪声影响

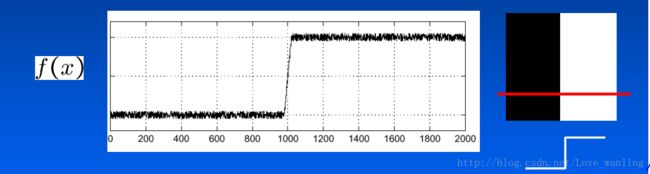
上图左侧是一维图像的表示，看似边界明显，但是由于有噪声的存在，是的求导之后的结果没有办法进行进一步操作，一阶导数图像如下：

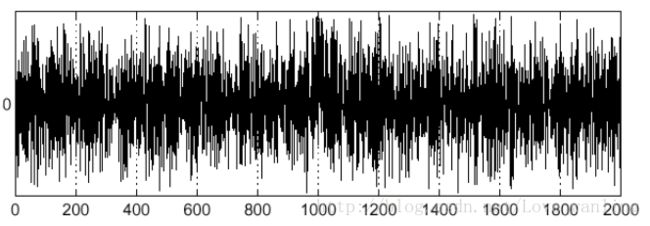
一团乱麻，根本没法找最大值，跟别说二阶导数求零点了。所以要去噪。我们用卷积来滤波。

这样最大值是不是就一目了然了(～￣▽￣)～。 另外卷积有性质，卷积的导数等于导数再卷积，所以可以简化成：

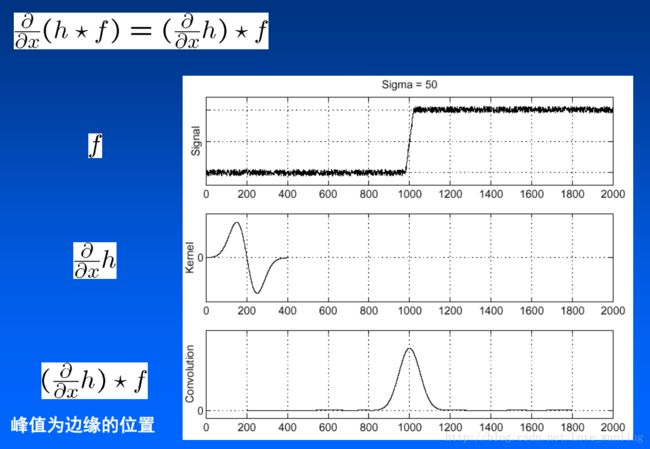
怎么样，是不是amazing。

图像梯度算子的近似

Prewitt算子

Prewitt算子近似一阶微分 将一列（行），变成了三列（行），达到平滑噪声的目的。

Sobel算子

近似一阶微分 去噪 + 增强边缘，给四邻域更大的权重

Laplace算子

这是一个二阶微分算子。我们先来看一下二阶微分在图像中怎么计算。
首先从二阶微分的定义入手：

f′′(x)=limx→0f′(x+Δx)−f′(x)Δx=limx→0f(x+Δx)−f(x)Δx−f(x)−f(x−Δx)ΔxΔx=limx→0f(x+Δx)−2f(x)+f(x−Δx)(Δx)2

在离散的图像中，则可以写成：

f′′(x)=f(x+1)−2f(x)+f(x−1)

所以一维的Laplaces算子为

二维形式推导如下：

所以

Laplacian of Gaussian

同样我们可以先进行高斯平滑，去除噪声，二阶导数到噪声太敏感了。


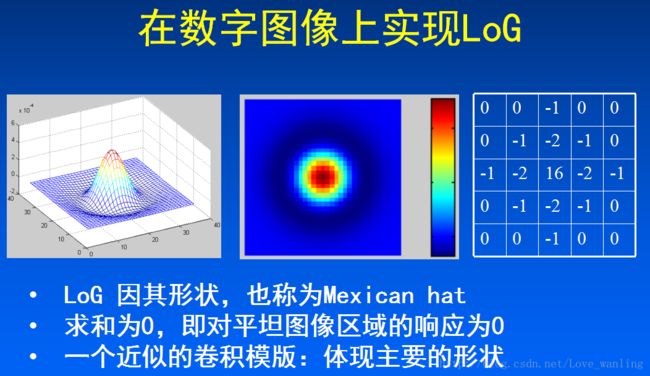
1. 中国科学院自动化研究所 董秋雷 课件
2. http://www.cnblogs.com/pegasus/archive/2011/05/20/2051780.html