关于音频数字信号分析一些简单知识点的提炼归纳
我们知道在时域上连续的数字信号,在每个时间点上都可以分解成不同频率的正玄波的叠加,即傅里叶变换。
关于fft请看这篇文章,如果上大学的时候老师都是这么讲课就好了啊。
https://mp.weixin.qq.com/s?__biz=MjM5MTIwMjY1Mg==&mid=2649870348&idx=1&sn=36b93232c0c2c7d3cdc38d275246c2a8&scene=2&srcid=0505d1dsi0t8guIdj5V2i3W2&from=timeline&isappinstalled=0#wechat_redirect
我们知道数字信号处理的主要数学工具就是傅里叶变换, 他的研究范围是整个时间域和频率域的关系,就如同卷积理论一样,先前发生的信号对后续的信号都会施加影响,只是间隔越远,影响越小而已。
对于计算机计算来讲,不可能对无限长的数据进行处理,只能对有限时间内的数据进行分析。
具体做法就是将数据在时间轴上截取一段,通过这一段波形我们来分析这个时间轴中心点那一时刻的频谱。
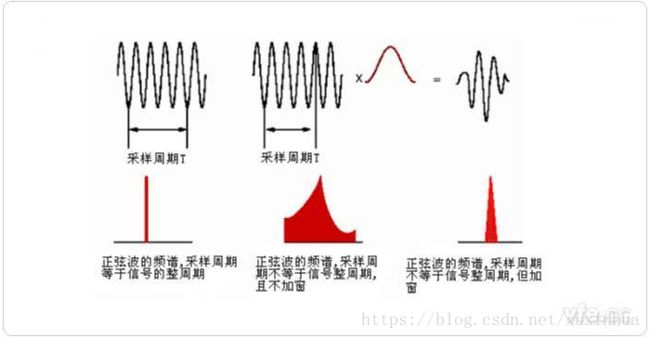
下图展示了一个周期信号截取数据后通过fft分析得出的频谱曲线:
从图上我们看到,如果我们采样周期刚好等于信号的整周期,则fft能够精确的分析出这段信号的频谱为一个单频率的信号。
但如果我们截取的数据不是信号的整周期(中间图),我们会发现fft分析出来的频谱和我们想的差别太大,其分析认为该采样为很多不同频率的信号叠加而成。
但实际信号中不可能出现第一种情况,每个信号都是多种频率的叠加信号,没法做到采样周期和信号周期同,故如果不对信号做处理直接做fft分析,分析出来的频谱和实际的频谱会出现较大的差异。
为了解决这个问题,我们对截取的分析信号做处理,即加窗处理,我们用另外一个窗信号和被分析信号进行叠加,为了强化越接近中心点,对信号影响越大,我们对信号进行数据加权处理,距离越远数据越小,这样在频率不变的情况下,影响越小。
第三种情况就是我们加了一种余玄函数类型的窗,两种数据相互作用产生一种两边为0的信号,我们延拓到无限域后就可以做fft分析,分析结果基本体现了源信号的频谱,虽然还有频谱泄露,但基本上反应了信号的频率属性,通过加窗我们可以改善频谱泄露,但不能完全消除。
窗函数有很多中,我们在fft分析前需要设定窗函数
output(t) = win(t)* source(t);
直接截取不做任何处理实际上就是矩形窗,即win(t)= 1.
另外还有很多知名的窗函数,如三角窗,各种余弦类型的窗,汉宁窗,海明窗,还有指数类型的高斯窗等。
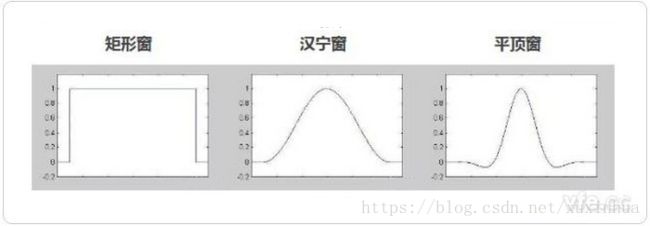
矩形窗、汉宁窗和平顶窗的时域形状和频域特征如下:
三种窗函数的时域形状
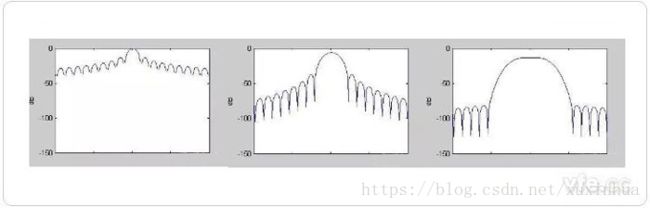
三种窗函数频域的特征
我们从图上可以看到第一图旁瓣分贝值很大,中间图旁瓣值小于-50分贝,已经很小了,中间部分相对比较瘦,最右边的,旁瓣更小,但中心区域很胖。
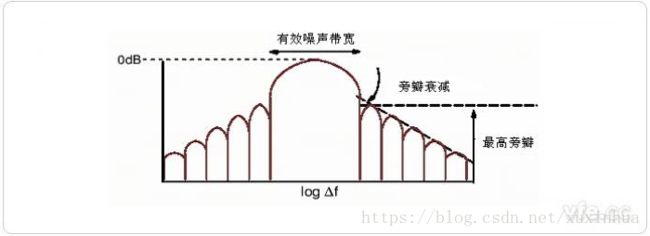
典型的窗函数特征
什么样的窗函数是好的窗函数?从频域特征我们来说明窗函数的数字信号。
1)主瓣宽度即有效噪声带宽应该越窄越好就如上图的汉宁窗就比平顶窗好。可以获得高的频率分辨力
2)旁瓣衰减应尽量大,这样平顶窗就比汉宁窗后,
由此可知没有任何窗能够最好,根据具体的需求选择不同的窗,汉宁窗基本上能够满足基本要求。
实际应用的例子:
48KHz的音频,每次解码器给出4096个采样,我们用来做频谱分析给出实时的频谱曲线
1)我们选择适当的窗函数,如汉宁窗,窗宽度为4096,我们生成hanning窗数组
2)用窗函数产生的数组做点积,就是和音频源数据逐个点相乘,窗第一个数乘以信号第一个数,如果被分析的采样数是4096,窗宽度就是4096,产生新的加窗后的数据。
3)我们对产生的加窗后的数据做fft变换,产生4096个频率数据,我们知道fft变换后,产生的数据有一半是镜像数据,故只有2048个有效数据。
48K采样率能够表达的频率最大是24Khz,奈奎斯特采样定理。
我们将0-24Khz的频率映射到2048个数据区间,fft变换出的频率是相对频率,如12K就是1024那个点的数据就是12K对应的功率。
所获得频率是时域中窗口中间时间的频率曲线,我们的窗大部分可以看出其中间时刻是最大值1,矩形窗除外。
要想取得某一时刻的频谱就必须以这个时刻为中心点获取左右两边的数据来通过fft计算获得。
加窗是给原始信号不同的权重对时间点来说,离分析的时间点越远影响越小,如卷积,越近信号施加的影响越大。
短时傅里叶变换和fft区别就是针对框宽度做几次,框越宽,时间分辨率越低,所含时间范围大,但包含的斌率信息就越多,频率分辨率就越高。框宽度减少,时间精度加大,包含的数据少,能分析的频率精度就少。就只能分析出高频部分,低频部分由于数据少,分析的就不精确了。但对于高频由于获取的影响参数少,反而更精确。
所以我们为了低频我们加大窗宽度,为了高频我们缩小窗宽度,stft我们可以取不同的窗宽度做六次用以获取不同频段的数据。
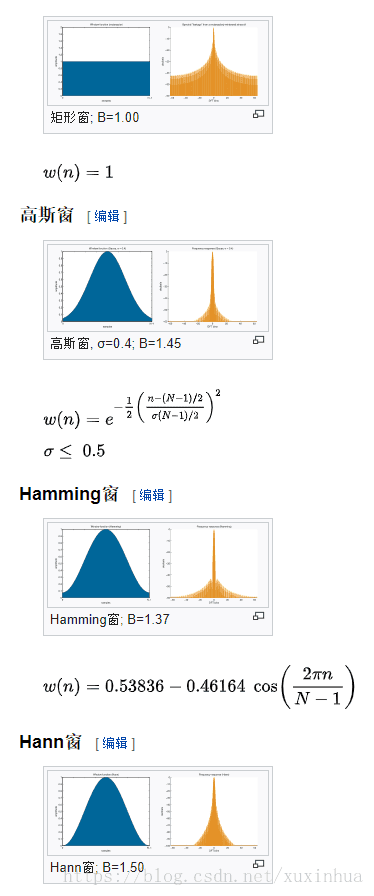
附录:窗函数图: