Sowu高精度详解
前言:在说高精度加减乘除运算之前,我们先搞明白什么是高精度运算?
利用计算机进行数值计算,有时会遇到这样的问题:有些计算要求精度高,希望计算的数的位数可达几十位甚至几百位,虽然计算机的计算精度也算较高了,但因受到硬件的限制,往往达不到实际问题所要求的精度。我们可以利用程序设计的方法去实现这样的高精度计算。
以下是几种常见数据类型的范围:
| 变量 | 范围 |
|---|---|
| int | -2147483648 ~ +2147483647 (4 Bytes) |
| char | -128 ~ +127 (1 Byte) |
| double | 1.7 * 10^308 (8 Bytes) |
| long long | -9223372036854775808 ~ +9223372036854775807 (8 Bytes) |
| unsigned long long | 0~18446744073709551615 |
简单说高精度就是处理要算的数太大或太小,没法直接储存计算的问题
其实高精度计算并不困难,只要需要处理好以下几个问题即可:
(1)数据的接收方法与位数的确定
(2)数据的存贮方法
(3) 进位,借位处理
(4) 商和余数的求法
(1)数据的接收方法与位数的确定:
当输入的数很大时,可采用字符串或者字符数组方法输入数据。前者我们用.size确定位数,后者采用strlen的方式确定位数
1、scanf读入字符串
#include2、gets读入字符串
char a[2020],b[2020]; //要定义char类型
gets(a);gets(b);
cout<<a<<" "<<b<<'\n';
int lena = strlen(a);
int lenb = strlen(b);
cout<<lena<<" "<<lenb;
3、cin读入字符串
string a,b;
cin>>a>>b;
cout<<a<<" "<<b<<'\n';
cout<<a.size()<<" "<<b.size();
scanf、cin遇空格或回车符则认为当前字符串结束
gets遇回车符则认为当前字符串结束
(2)数据的存贮方法:
关于数据的储存,我们可以利用字符串函数和操作运算,将每一位数取出,存入数组中
string a;
int num[2020];
cin>>a;
int lena = a.size();
for(int i = 1;i <= lena;i ++)
num[i] = a[i - 1] - '0';
for(int i = 1;i <= lena;i ++)
cout<<num[i];
(3) 进位,借位处理
加法进位:
a[i] += b[i] + c[i];
if(a[i] >= 10)
{
a[i + 1] ++;
a[i] %= 10;
}
减法借位:
a[i] += b[i] - c[i];
if(a[i] < 0)
{
a[i + 1] --;
a[i] += 10;
}
乘法进位:
a[i + j - 1] += a[i] * b[j];
if(a[i] > 10)
{
a[i + 1] += a[i] / 10;
a[i] %= 10;
}
(4) 商和余数的求法
数据较小时高精除可以用减法来模拟除法,对被除数的每一位都减去除数,一直减到被除数小于除数,运算次数为商,剩余的被除数为余数
数据较大时
待添加
模板:
高精度加法(必做) :https://www.luogu.com.cn/problem/P1601
高精度减法(必做) :https://www.luogu.com.cn/problem/P2142
高精度乘法(必做):https://www.luogu.com.cn/problem/P1303
高精度除法 (选做):https://www.luogu.com.cn/problem/P5432
高精度开跟 (选做): https://www.luogu.com.cn/problem/P2293
高精求小数幂(选做):https://www.luogu.com.cn/problem/P1517
【模板1 高精度加法】
题目:
洛谷 P1601 A+B Problem(高精)
详解1:
1、数据处理:先将两大数存入字符串,再将字符串每一位转为数字存入数组
//将两数存入字符串a,b;再转为数字存入数组num1,num2
cin >> a >> b;
int len1 = strlen(a);
int len2 = strlen(b);
int numlen = 0, i;
for (i = 0; i < len1; i++)
num1[i] = a[i] - '0';
for (i = 0; i < len2; i++)
num2[i] = b[i] - '0';
2、将数组num1和num2按位数依次倒序相加,存入新数组num。
例:个位对应num1[len1-1]、num2[len2-1],需将两者相加存入新数组num[0]中
for (i = 0; len1 > 0 || len2 > 0; i++) {
if (len1 > 0 && len2 > 0)
{
num[i] += num1[len1 - 1] + num2[len2 - 1];
len1--, len2--;
}
else if (len1 == 0)//len1位数比len2少时
{
num[i] += num2[len2 - 1];//只加len2
len2--;
}
else if (len2 == 0)
{
num[i] += num1[len1 - 1];
len1--;
}
if (num[i] >= 10)//加法进位
{
num[i + 1]++;
num[i] %= 10;
}
}
3、得到答案,倒序输出。注意最后一位进位的情况
numlen = i;
if (num[numlen] > 0)//注意若最后一位有进位,最后数组总长度要加1
numlen++;
for (i = numlen - 1; i >= 0; i--)
cout << num[i];
详解2
1、数据处理
char a[2000],b[2000];
int x[2000],y[2000],z[2000];
int num=0;
int len2=0;
memset(z,0,sizeof(z));//初始化一下
memset(x,0,sizeof(x));
memset(y,0,sizeof(y));
scanf("%s%s",a,b);
int lena=strlen(a);
int lenb=strlen(b);
int len=lena>lenb?lena:lenb;//比较大小求出最长的长度
for(int i=0;i<lena;i++)
{
x[i]=a[lena-i-1]-'0';//字符型数字化成整型数字(倒序)
}
for(int i=0;i<lenb;i++)
{
y[i]=b[lenb-i-1]-'0';
}
2、数组相加 (注意进位问题即可)
for(int i=0;i<len;i++)
{
z[i]=x[i]+y[i]+num;//相加
num=z[i]/10;//判断进位,若在z[i]>=10,num=1,若z[i]<10,num=0
z[i]=z[i]%10;
len2++;
}
if(num)//num=1,末位进位,将1赋给len2位置
{
z[len2]=num;
}
else//num=0,无进位,长度减1即可
{
len2--;
}
3、倒序输出
for(int i=len2;i>=0;i--)
{
printf("%d",z[i]);
}
return 0;
【模板2 高精度减法】
题目:洛谷 P2142 高精度减法
详解:
1、数据处理:同上,略
2、判断结果正负和答案为0的情况:
可以先写个函数判断一下答案正负情况,
int F() {
if (len1 > len2)
return true;//答案为正的情况返回true
else if (len1 == len2)
{
int i=0, j =0;
while (num1[i] == num2[j])
{
i++, j++;
if (i == len1)//注意不要忘记两数相等的情况
return 2;//答案为0返回标记为2
}
if (num1[i] > num2[j])
return true;
else
return false;
}
else
return false;//答案为负的情况返回false
}
若结果为负,可先反过来减,最后输出时加上负号
//若结果为负可交换一下两数位置,反过来减
if (!flag) {
for (i = 0; i < len1; i++) {
int x = num1[i];
num1[i] = num2[i];
num2[i] = x;
}
while (i < len2)
{
num1[i] = num2[i];
i++;
}
int y = len1;
len1 = len2, len2 = y;
}
3、对应位数相减(会了高精度加法的话减法应该不成问题~我就不详细分析啦)
for (i = 0;len2 > 0||len1>0; i++) {
if(len2>0)
{
num[i] += num1[len1 - 1] - num2[len2 - 1];
len1--, len2--;
}
else if (len2 <= 0)
{
num[i] += num1[len1 - 1];
len1--;
}
if (num[i] < 0)//减法借位
{
num[i + 1]--;
num[i] += 10;
}
}
4、输出结果。
numlen = i;
if(flag==2)//答案为0的情况
cout << 0;
else
{
if (!flag)//答案为负时记得输出负号
cout << "-";
while (num[numlen - 1] == 0)//前缀有0需消除
numlen--;
for (i = numlen - 1; i >= 0; i--)
cout << num[i];
}
【模板3 高精度乘法】
题目:洛谷 P1303 A*B Problem
详解(参考博客:点我):
核心代码
for (i = 1; i <= len1; i++)
{
for (j = 1; j <= len2; j++)
{
num[i + j - 1] += num1[i] * num2[j];
num[i + j] += num[i + j - 1] / 10;
num[i + j - 1] %= 10;
}
}
分析
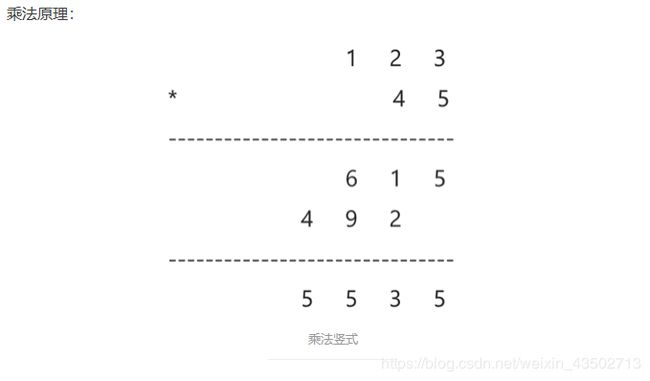
核心代码(乘法运算部分)是由模拟乘法竖式算出来的:
(1) 数1的倒数第i位与数2的倒数第j位相乘所得到的值应存在结果的倒数第i+j-1位上。
(2) 如果结果的i+j-1位大于9,则进位到i+j位。
举例 :比如说当i=j=1、即num1[i]=3,num2[j]=5时,
num[i+j-1]=num1[1]*num2[1]%10=5;
num[i+j] + =num1[1]*num2[1]/10=0+1=1;
即当前:num[1]=5,num[2]=1(后续这个num[2]还会继续累加,对应举例中标黄部位);
需注意的地方:
1、高精度乘法进位的掌握~~
2、i位数 与 j位数 相乘,其结果最多为 i+j 位。
3、注意答案为0的情况和前缀有0的情况。
附:高精度加、减、乘法模板题AC代码 自己写的可能有些地方不够简洁规范,仅供参考哈~
【模板4 高精度除法】
精简核心代码
// A / b = C ... r, A >= 0, b > 0
vector<int> div(vector<int> &A, int b, int &r)
{
vector<int> C;
r = 0;
for (int i = A.size() - 1; i >= 0; i -- )
{
r = r * 10 + A[i];
C.push_back(r / b);
r %= b;
}
reverse(C.begin(), C.end());
while (C.size() > 1 && C.back() == 0) C.pop_back();
return C;
}
分析
算法的步骤如下:
1、将除数移动和被除数对齐,位数不够时,补0。
2、利用被除数减去除数,一直减到被除数小于除数,减的次数,就是“试商”的结果,每移动一次。
3、重复上述步骤,一直到被除数和除数的位数相等为止。
待添加
好题:
B进制 (选做):https://www.luogu.com.cn/problem/P1604
1.数据处理
int a[2010], b[2010];
char m[2010], n[2010];
cin >> B;//进制数
cin >> m; cin >> n;
l1 = strlen(m);
for (i = 0; i < l1; i++)
{
if (B > 10 && m[i] >= 'A')
a[l1 - i] = m[i] - 'A' + 10;//字符串逆序存储
else
a[l1 - i] = m[i] - '0';//遇到字母转换成数字
}
//对于字符数组n同上处理,放入整形数组b中
2.高精度加法
x=0,y=0;//x是位数,y是进位
while (x <= l1 || x <= l2)
{
x++;
ans[x] = y + a[x] + b[x];
y = ans[x] / B;
ans[x] %= B;
}
3.输出
//去除前置位的零
while (ans[x] == 0 && x > 1)
x--;
//输出
for (i = x; i >= 1; i--)
{
if (ans[i] < 10)
cout << ans[i];
else
cout << (char)(ans[i] + 'A' - 10);
}
待添加
模板及详解:
待添加
编写人:
- Sowu_lion
- Sowu_0077
- Sowu_zxt
- Sowu_Qing