Tree, priority queue and BST (python)
一.建立树结构:
在自定义的二叉树内,我们需要保存当前节点的值,其左子树和其右子树。同时还需定义插入函数,注意插入函数定义时需要考虑是否当前节点已经有了左子树或右子树,若已经存在,则应该在插入新节点后接上原子树。
class BinaryTree:
def __init__(self, root):# initialization
self.key = root
self.leftChild = None
self.rightChild = None
def insertLeft(self, newNode): # consider two situations, if current node has a left child or not
if self.leftChild == None:# if root doesn't have a left child
self.leftChild = BinaryTree(newNode)
else:# if it has a left child
t = self.leftChild
self.leftChild = BinaryTree(newNode)
self.leftChild.leftChild = t
def insertRight(self, newNode): # same as above
if self.rightChild == None:
self.rightChild = BinaryTree(newNode)
else:
t = self.rightChild
self.rightChild = BinaryTree(newNode)
self.rightChild.rightChild = t
def getRoot(self): # get funcion
return self.key
def setRoot(self, val): # set function
self.key = val
def getLeft(self):
return self.leftChild
def getRight(self):
return self.rightChild二. 如果使用树结构
经典使用方法:将四则运算变换成树结构。
通过观察,我们设定一系列法则:
1. 假如遇到" ( ",我们建立左子树,然后进入左子树。
2. 假如遇到数字,我们将当前的node的value设置为该数字,接着返回父节点。
3. 假如遇到运算符(+,-,*,/),我们将当前节点的value设置为该运算符,接着进入右节点。
4. 假如遇到")",返回父节点。
我们可以用过数据结构很简单的得到子节点,但是如何得到父节点?
一个好的方法是使用stack来存储当前节点,当进入子节点时,将父节点入栈。当返回父节点时,将父节点出栈。
#代码来源https://runestone.academy/runestone/books/published/pythonds/Trees/ParseTree.html
from pythonds.basic import Stack
from pythonds.trees import BinaryTree
def buildParseTree(fpexp):
fplist = fpexp.split()
pStack = Stack()
eTree = BinaryTree('')
pStack.push(eTree)
currentTree = eTree
for i in fplist:
if i == '(':
currentTree.insertLeft('')
pStack.push(currentTree)
currentTree = currentTree.getLeftChild()
elif i in ['+', '-', '*', '/']:
currentTree.setRootVal(i)
currentTree.insertRight('')
pStack.push(currentTree)
currentTree = currentTree.getRightChild()
elif i == ')':
currentTree = pStack.pop()
elif i not in ['+', '-', '*', '/', ')']:
try:
currentTree.setRootVal(int(i))
parent = pStack.pop()
currentTree = parent
except ValueError:
raise ValueError("token '{}' is not a valid integer".format(i))
return eTree解析树结构:
使用递归的方法来进行计算,因为我们的目标是 (左子树) -> (父节点 加减乘除) -> (右子树),所以我们是中序遍历LNR
递归的方法是,遇到一个节点,获得左节点的值A, 获得当前节点的操作符op,获得右节点的值B:
return op(A,B)
#代码来源https://runestone.academy/runestone/books/published/pythonds/Trees/ParseTree.html
def evaluate(parseTree):
opers = {'+':operator.add, '-':operator.sub, '*':operator.mul, '/':operator.truediv}
leftC = parseTree.getLeftChild()
rightC = parseTree.getRightChild()
if leftC and rightC: #如果有左右节点,说明有计算
fn = opers[parseTree.getRootVal()]
return fn(evaluate(leftC),evaluate(rightC))
else:# 递归出口: 如果是叶子节点,则返回当前的数字
return parseTree.getRootVal()
三. 遍历树:前序,中序,后序
1. preorder: 遇到一个节点,先读取当前节点,然后递归访问左子树,最后递归方位右子树。
2. inorder: 遇到一个节点,先递归访问左子树,然后访问当前节点,最后递归访问右子树。
3. postorder: 遇到一个节点,先递归访问左子树,然后递归访问右子树,最后访问当前节点。
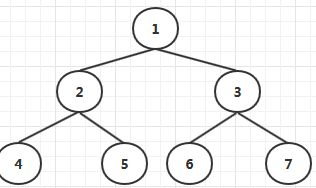
前序遍历: 1, 2, 4, 5, 3, 6, 7 (中,左,右)
中序遍历: 4, 2, 5, 1, 6, 3, 7 (左,中,右)
后序遍历: 4, 5, 2, 6, 7, 3, 1 (左,右,中)
def traversePreorder(ptr):
if ptr == None: # exit
return
else:
print(ptr.getRoot()) #中
traversePreorder(ptr.getLeft()) #左
traversePreorder(ptr.getRight()) # 右
def traverseInorder(ptr):
if ptr == None:#exit
return
else:
traverseInorder(ptr.getLeft()) # 左
print(ptr.getRoot()) # 中
traverseInorder(ptr.getRight()) # 右
def traversePostorder(ptr):
if ptr ==None:#exit
return
else:
traversePreorder(ptr.getLeft()) # 左
traversePreorder(ptr.getRight()) # 右
print(ptr.getRoot())#中完全二叉树:除了叶子节点,其他部分是满二叉树。
四.优先序列(二进制堆) priority queue with binary heap
作用:输入无序的数组,得到有序的优先序列,并且新加入的值可以自动排序
enqueue和dequeue都是O(lgn)复杂度
使用一个list来实现该队列,同时使用优先二叉树的思维:
一个位置为p的节点,它的左子树的节点是 2p,右子树是2p + 1。
Heap Order Priority: 一个数的子节点一定大于或者等于父节点(保证了根节点一定存着最小的值)
1. 初始化binaryHeap
1.1 使用一个list来保存元素,同时存储当前bh的大小。
class binaryHeap:
def __init__(self):
self.heapList = [0]
self.currentSize = 0(注意我们在list的头上插入一个0,是为了方便进行除法操作)
1.2 插入操作 insert
首先在尾部append进入list内,然后通过比该新增元素和其父节点的关系来进行swap操作,从而保证优先序列的优先级。
def insert(self, val):
self.heapList.append(val)
self.currentSize += 1
i = len(heapList) - 1
while i // 2 > 0:
if self.heapList[i // 2] < self.heapList[i]:
temp = self.heapList[i // 2]
self.heapList[i // 2] = self.heapList[i]
self.heapList[i] = temp
i = i // 21.3 删除操作 deleteMin
因为优先序列保证了根节点是最小值,我们直接删除根节点,然后将尾部的值放到根节点。然后sink下去: 如果parent的key小于子节点中的“更大的”, 则将他俩交换,继续下去。
def percDown(self,i):
while (i * 2) <= self.currentSize:
mc = self.minChild(i)
if self.heapList[i] > self.heapList[mc]:
tmp = self.heapList[i]
self.heapList[i] = self.heapList[mc]
self.heapList[mc] = tmp
i = mc
def minChild(self,i):
if i * 2 + 1 > self.currentSize:
return i * 2
else:
if self.heapList[i*2] < self.heapList[i*2+1]:
return i * 2
else:
return i * 2 + 1
def delMin(self):
retval = self.heapList[1]
self.heapList[1] = self.heapList[self.currentSize]
self.currentSize = self.currentSize - 1
self.heapList.pop()
self.percDown(1)
return retval五. 二分搜索树 Binary Search Tree
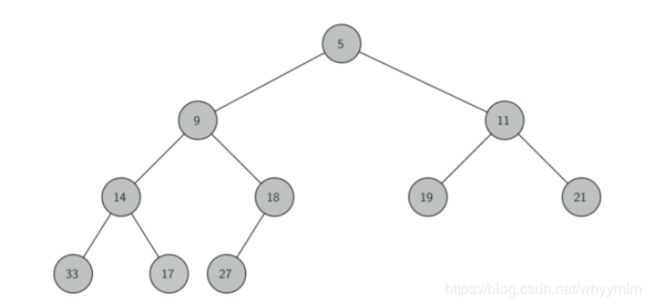
二分搜索树的左子树小于根节点,右子树大于根节点
插入和搜索的复杂度: o(lgn)
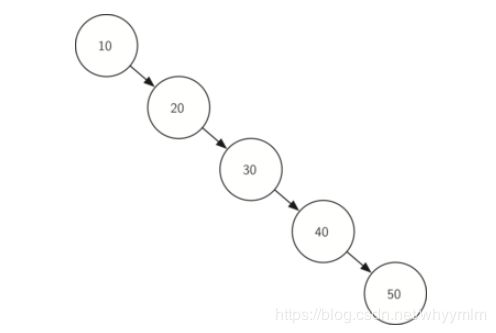
但是当搜索树建立的不好时,也会degrade到O(n):
二叉搜索树:
1. insert
def insertIntoBST(self, root, val):
def goDown(ptr, val):
if val < ptr.val:
if ptr.left!= None:
goDown(ptr.left, val)
else:
ptr.left = TreeNode(val)
else:
if ptr.right != None:
goDown(ptr.right, val)
else:
ptr.right = TreeNode(val)
goDown(root, val)2.delete
首先从root一直找到需要删除的位置,然后针对要被删除的节点,需要考虑三种情况:
1.如果该节点没有子节点
直接对该节点进行删除操作即可。
2.如果该节点有一个子节点
只需要把它接上即可,(需要在搜索的时候返回到底该节点是父节点的左节点还是右节点)。
3.如果该节点有两个子节点
需要找到一个节点和他交换。同时删除那个需要交换的节点。
该节点是右子树的最小值节点。
In order to buld a balanced binary search tree, we use AVL Tree.
AVL Tree:
AVL tree makes sure that it is a blanced binary search tree all the time.
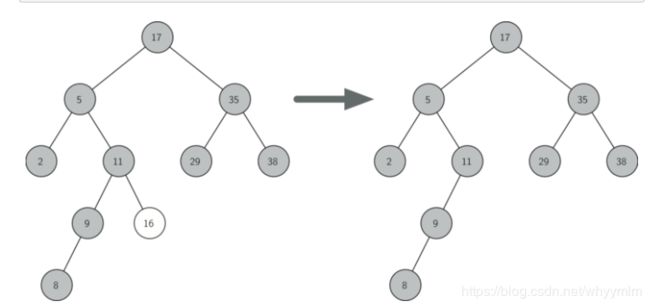
当AVL树加入新节点时,需要对树进行变换:
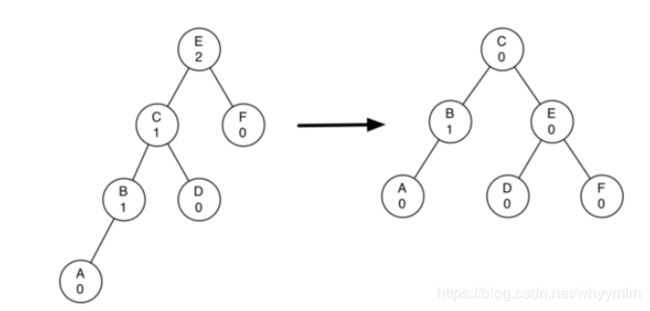
1.左左型或右右型
当前不平衡点是E
1.将E的左子树变为新的根节点
Promote the left child (C) to be the root of the subtree.
2.将老根节点E变为新根节点的右子树
Move the old root (E) to be the right child of the new root.
3.如果C原本有右子节点,则将它变成E的左节点(譬如图中的D节点)
If the new root(C) already had a right child (D) then make it the left child of the new right child (E). Note: Since the new root (C) was the left child of E, the left child of E is guaranteed to be empty at this point. This allows us to add a new node as the left child without any further consideration
2.左右型或右左型
此时A的平衡度是-2,但是它不应该直接使用左旋。我们应把它先变成正常的右右型再左旋。
先将该子树右旋,再左旋