剑指offer二叉树题型解析
题目四:输入某二叉树的前序遍历和中序遍历的结果,请重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6},则重建二叉树并返回。
解析:前序遍历的顺序是中左右,而中序遍历的序列是左中右,所以在第一个序列中1肯定是整个树的根节点,而通过中序遍历序列找到整个1,那么1左边的肯定就是左子树,1右边的肯定是右子树,图示如下:

可以看到,在第一步中就可以将根节点和左子树和右子树找到,第二步就可以继续对左子树和右子树进行同样的操作,可以看出这是很明显的递归程序。
代码如下:
public TreeNode reConstructBinaryTree(int [] pre,int [] in) {
return ConstructBinaryTree(pre,0,pre.length-1,in,0,in.length-1);
}
public TreeNode ConstructBinaryTree(int[] pre,int sp,int ep,int[] in,int si,int ei) {
if (sp>ep||si>ei) {
return null;
}
//通过前序序列获取到根节点的值
int rootV = pre[sp];
//在中序序列中通过跟节点的值获取到跟节点的索引
int index = si;
while(index<=ei){
if (rootV == in[index]) {
break;
}
index++;
}
if (index>ei) {
throw new RuntimeException("error...");
}
//新建节点等于这个跟节点
TreeNode node = new TreeNode(rootV);
//索引左边的是跟节点的左子树,右边是跟节点的右子树
int leftCount = index-si;
int rightCount = ei-index;
//对左右子树进行递归
node.left = ConstructBinaryTree(pre, sp+1, sp+leftCount, in, si, index-1);
//返回新建的节点
node.right = ConstructBinaryTree(pre, sp+leftCount+1, ep, in, index+1, ei);
return node;
}
这个代码的关键是后面递归的时候确定出坐标值,如果觉得难想,那么可以在纸上画出图进行分析。
题目十七:输入两棵二叉树A,B,判断B是不是A的子结构。(ps:我们约定空树不是任意一个树的子结构)。
解析:首先通过一个图形:

如图所示,左边的图是包含了右边的图的,而判断一个树是不是包含另一个树,首先得要判断根节点是不是相等,如果根节点不相等,那么就遍历这个树看下一个节点是否相等,如果找到了相同的节点那么第二步则判断这个根节点相同的树的子树是否相等,也就是判断节点是相等,如果子树不相等,那么在第一步中继续遍历下一个节点找出相同的节点。这里可以看出要写两个递归函数,第一个递归函数用来找根部相同的点,第二个递归函数用来判断根部相同点的子树是否相等。代码如下:
public boolean HasSubtree(TreeNode root1,TreeNode root2){
if (root1==null||root2==null) {
return false;
}
boolean res = false;
//若根节点相等,那么进行子树结构判断
if (root1.val == root2.val) {
res = Tree1IsHaveTree2(root1,root2);
}
//如果根节点不相等或者根节点相等但是子树不相等,那么遍历这个数继续判断
if(!res){
//在左子树和右子树中寻找,有一个返回true那就说明包含了
res = HasSubtree(root1.left, root2)||HasSubtree(root1.right, root2);
}
return res;
}
public boolean Tree1IsHaveTree2(TreeNode root1,TreeNode root2){
//如果第二个树已经没有节点了,那么说明其余的节点都相等
if (root2 == null) {
return true;
}
//如果第一个树没有节点了,那么说明肯定不相等
if (root1 == null) {
return false;
}
//如果节点值不相同,那么也不相等
if (root1.val != root2.val) {
return false;
}
//如果相等,那么继续对左边的节点和右边的节点进行判断。两边的节点必须都一直才返回true
return Tree1IsHaveTree2(root1.left,root2.left)&&Tree1IsHaveTree2(root1.right,root2.right);
}
题目十八:操作给定的二叉树,将其变换为源二叉树的镜像。
解析:这个题的图示如下:
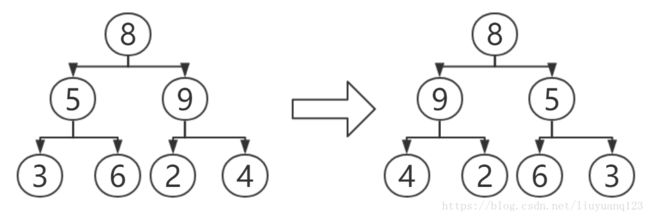
可以看出镜像二叉树其实就是将所有节点的左右子树交换即可,这里可以一层一层的交换,也可以用递归进行实现。从根节点开始逐一交换。代码如下:
//判断节点是否为空
if(root == null)
return;
//如果不为空则交换左右子节点
TreeNode node = root.left;
root.left = root.right;
root.right = node;
//遍历左子树和右子树实现相同操作
Mirror(root.left);
Mirror(root.right);
题目21:从上往下打印出二叉树的每个节点,同层节点从左至右打印。
解析:图示:

如图可以看出,可以建立一个辅助队列用于存储节点,首先将根节点存入,然后判断队列是否为空,不为空就将队列头出队列,在将出队列的节点的子节点入队列,如图所示,一直这样便可以从上到下从左到右打印出子节点。代码如下:
public ArrayList PrintFromTopToBottom(TreeNode root){
ArrayList list = new ArrayList<>();
//判断节点是否为空
if (root==null) {
return list;
}
//不为空建立队列将这个节点入队列
Queue queue = new LinkedList<>();
queue.offer(root);
TreeNode node = null;
//当队列不为空的时候讲节点出队列,并将节点的子节点入队列
while(queue.size()>0){
node = queue.poll();
list.add(node.val);
if (node.left != null) {
queue.offer(node.left);
}
if (node.right!=null) {
queue.offer(node.right);
}
}
return list;
}
题目22:输入一个整数数组,判断该数组是不是某二叉搜索树的后序遍历的结果。如果是则输出Yes,否则输出No。假设输入的数组的任意两个数字都互不相同。
解析:这个题目和题目三的重建二叉树其实是类似的,后序遍历的遍历顺序是左右中,所以根节点是放在后面的,序列的最后一个点是整个树的根节点,所以第一步可以找到根节点,然后再判断序列中从左到右哪个节点的值大于了这个点,那么这个节点之前的点就是左子树,这个节点及之后并在根节点之前的节点是右子树,所以只需要判断右子树中有不有小于根节点的点,如果有的话,那么不可能是后序序列,如果没有,那么则继续对左子树和右子树进行相同的操作,也就是递归实现,图示:
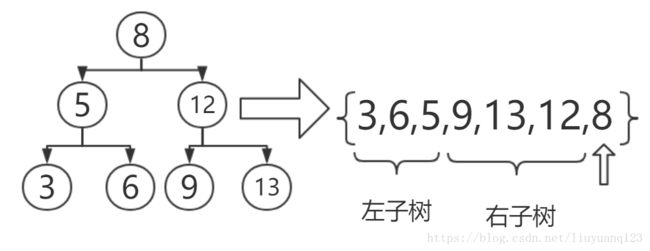
代码如下:
public boolean VerifySquenceOfBST(int [] sequence) {
if(sequence == null||sequence.length<=0)
return false;
return Verify(sequence, 0, sequence.length-1);
}
public boolean Verify(int [] sequence,int start,int end) {
//获取左子树
boolean left = true;
boolean right = true;
int index = start;
int root = sequence[end];
while(indexroot) {
break;
}
index++;
}
//判断右子树中是否有小于根节点的节点
for (int i = index; i < end; i++) {
if (sequence[i] 题目23:输入一颗二叉树和一个整数,打印出二叉树中结点值的和为输入整数的所有路径。路径定义为从树的根结点开始往下一直到叶结点所经过的结点形成一条路径。
解析:首先要明确题目中的路径,路径是指根节点到子节点经过的节点,意思是路径必须要包含子节点。在前序遍历中会从根节点到达所有的子节点,所以这个题目可以通过前序遍历实现,在遍历过程中,将当前节点加入到路径中,并且设定一个累减值,将累减值减去当前节点的值,如果这个值为0并且已经到达子节点,那么就将路径加入到列表中,然后继续对遍历,每次递归退出的时候记得在路径中去掉当前节点。代码如下:
ArrayList> resultList = new ArrayList<>();
ArrayList list = new ArrayList<>();
public ArrayList> FindPath(TreeNode root,int target) {
//首先判断节点是否为空,目标值是否大于0
if(root==null||target<=0)
return resultList;
//建立一个目标值和将当前节点累减,并将当前节点加入到路径中
int sum = target;
sum -= root.val;
list.add(root.val);
//如果这个累减值等于了0并且当前节点为子节点,那么将这个路径加入到list中
if (sum==0&&root.left==null&&root.right==null) {
resultList.add(new ArrayList<>(list));
//如果不满足,那么就继续递归遍历累减
}else {
FindPath(root.left,sum);
FindPath(root.right,sum);
}
//递归返回后将路径中最后一个节点也就是开始加入的节点去掉
list.remove(list.size()-1);
return resultList;
}
这里有个注意的地方就是resultList.add(new ArrayList<>(list));每次加入的路径都必须新建一个路径,否则,list会一直改变的。
题目27:输入一棵二叉搜索树,将该二叉搜索树转换成一个排序的双向链表。要求不能创建任何新的结点,只能调整树中结点指针的指向。
解析:图示:
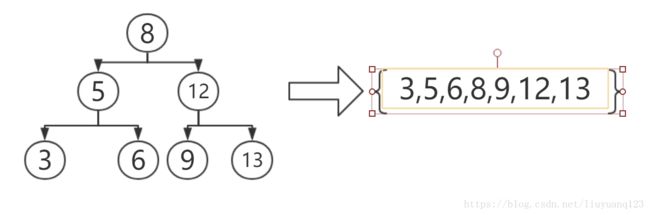
可以看到,如果把二叉树转化为链表,那么链表中的顺序应该是这样的,而右边这个序列其实是二叉树的中序遍历序列,所以要将二叉树转化为链表,可以在中序遍历的基础上实现节点指向的改变,这里设定一个链表的指向节点,也是二叉树的指向节点,首先,对二叉树递归找到左边的子节点,然后将该节点指向链表节点,如果链表节点不为空了,说明已经指向了二叉树的某个节点,那么将链表节点的右节点指向当前树的节点,然后递归找右节点,最后返回这个链表节点即可。代码如下:
public TreeNode Convert(TreeNode pRootOfTree) {
if (pRootOfTree==null) {
return pRootOfTree;
}
TreeNode lastNode = ConvertTreeToList(pRootOfTree,null);
TreeNode firstNode = lastNode;
while(firstNode!=null && firstNode.left!=null){
firstNode = firstNode.left;
}
return firstNode;
}
public TreeNode ConvertTreeToList(TreeNode pRootOfTree,TreeNode listNode){
//判断节点是否为空
if(pRootOfTree == null)
return listNode;
//中序遍历遍历到左边子节点
listNode = ConvertTreeToList(pRootOfTree.left,listNode);
//将当前节点的left指向listNode,如果listNode不为空,将listNode的right节点指向当前节点
TreeNode cNode = pRootOfTree;
cNode.left = listNode;
if (listNode!=null) {
listNode.right = cNode;
}
//将listnode指向下一个节点
listNode = cNode;
//中序遍历遍历到右边子节点
listNode = ConvertTreeToList(pRootOfTree.right,listNode);
return listNode;
}
未完待续。。。。。。。。。