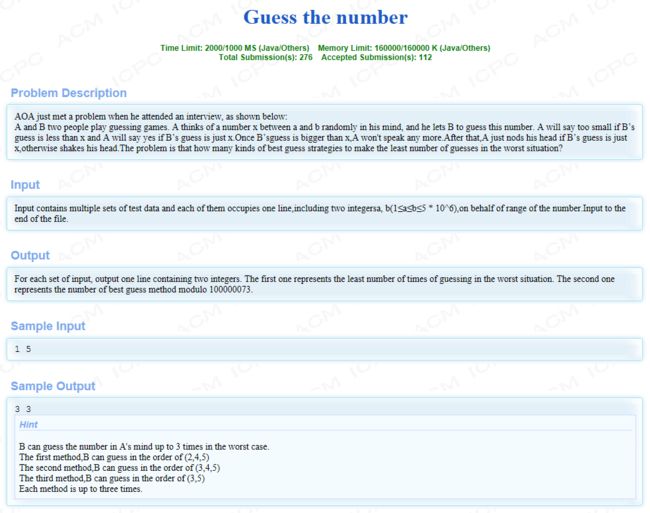
HDU 5981 && 2016ICPC大连 K: Guess the number(推理)
题意:
A在[L, R]之间随机选取一个数X,之后B来猜这个数,如果猜的数比X小,那么A就告诉B猜小了,如果猜的数大于X,那么以后A永远只会回答B是否猜对了,问在最坏的情况下B至少要猜多少次,并求出有多少种方案
在[L, R]之间猜数同等于在[1, R-L+1]之间猜数,那么就当做在[1, R]之间猜数吧
问题反过来想,假设B只有1次猜的机会,那么在保证B可以猜对的情况下R最大能是多少?(废话肯定R只能为1)
那假设B只有k次猜的机会,在保证B可以猜对的情况下R最大能是多少?
假设当前B猜的数是p,如果p>X,那么完蛋以后P只能从1猜到p-1,所以B第一次必须猜小于等于k的数
这样也显然猜k就好了,就算k>X,从1猜到k-1也最多k-1次就可以猜对
若k
同理若k+k-1
这样模型和答案就都出来了,假设B只有k次猜的机会,那么允许最大的R就是(1+k)*k/2
那么这题的第一个问题就解决了,对于[L, R],只要找到最小的满足(1+k)*k/2>=R-L+1,k就是答案
难在有多少种方案
……
其实也不难,令p[R]表示范围[1, R]是的最优猜测次数
more[i]表示在保证B猜i次一定可以猜对的情况下R最大能是多少
cnt[R]表示范围[1, R]的最优猜测方案数,sum[]是cnt[]的前缀和
那么对于当前的R,主要是看B第一次可以猜哪些数,这样问题就可以变成子问题递推解决
很显然B猜完第一个数之后剩下的规模一定要小于more[p[R]-1],否则就无法最优了,而剩下的规模可以是0到more[p[R]-1]中的任意一种,所以cnt[R] = ∑cnt[more[p[R]-1]] = sum[more[p[R]-1]]
可是这样不对,别忘了你第一次猜的数不能大于p[R]!!
所以有cnt[R] = sum[more[p[R]-1]]-sum[R-p[R]-1]
预处理1到5000000的p[]和cnt[],每次询问[L, R],答案就是p[R-L+1],cnt[R-L+1]
#include
#define mod 100000073
int p[5000005], more[5005], cnt[5000005] = {0,1}, sum[5000005] = {1,2};
int main(void)
{
int l, r, i, j;
for(r=1,i=1;i*(i-1)/2<=5000000;i++)
{
for(j=i*(i-1)/2+1;j<=i*(i+1)/2 && j<=5000000;j++)
p[j] = i;
more[i] = i*(i+1)/2;
}
for(i=2;i<=5000000;i++)
{
cnt[i] = (sum[more[p[i]-1]]-sum[i-p[i]-1]+mod)%mod;
sum[i] = (sum[i-1]+cnt[i])%mod;
}
while(scanf("%d%d", &l, &r)!=EOF)
printf("%d %d\n", p[r-l+1], cnt[r-l+1]);
return 0;
}