LCA实现的三种不同的方法

LCA，最近公共祖先，实现有多种不同的方法，在树上的问题中有着广泛的应用，比如说树上的最短路之类。

LCA的实现方法有很多，比如RMQ、树链剖分等。今天来讲其中实现较为简单的三种算法：RMQ+时间戳、树上倍增（类似二分步长）、Tarjan算法（DFS+并查集）。

【RMQ+时间戳】

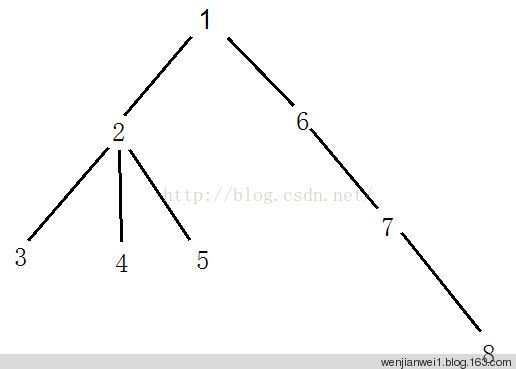
什么是时间戳？时间戳，就是被访问到的一个次序。比如说我们首先对一棵树进行深搜，在深搜中访问的相应次序就被我们称为时间戳。比如说对下面这棵树进行相应的深搜，我们得到时间戳，以及相应的遍历序列：

 

 

这棵树所得到的DFS遍历序列就是1 2 3 2 4 2 5 2 1 6 7 8 7 6 1。可以看出，每个非叶节点都被访问了不止一次。好了，时间戳讲完了，接着转入正题：怎样用RMQ？RMQ在这里是我们算法的一个极为重要的基础，具体有什么不明白可以看我以前的博客《Sparse-Table算法 - 一类RMQ问题的简单高效解法 》。

既然我们得出了这么一个序列，要RMQ，就是对这一个序列进行。而这个思路是正确的。如果我们对于每一个节点，都只记这一个节点在DFS序列中第一次出现的位置，比如说节点1，第一次就是在位置1，节点6，第一次就是在位置10，以此类推。然后我们对这么一个DFS序列作RMQ的最小值预处理，然后对于LCA的每次询问，只需求这两个被询问节点在DFS序列中第一次出现的位置构成的区间内的最小值即可。时间复杂度加上预处理，应该是O(Nlog2N+Qlog2N)的时间复杂度（虽然说实际上来说RMQ的单次询问是和O(1)相当的，但实际上的规模是O(log2N)，如果另外处理一个常数表，占用空间可能挺大的，毕竟直接实现的速度也挺快的）。举个例子，我们要询问节点6和8的LCA，则节点6的首次出现位置是10，节点8的首次出现位置是12，则区间[10,12]中的最小值是6，那么他们的LCA就是节点1。

那么，为什么这样会可以呢？考虑一下我们深搜的过程，寻求两个节点的LCA朴素过程其实可以转变成这样的形式：从其中一个节点出发，一直往上找，并不断遍历以当前找到的结点为根的子树，看有没有同时包含两个节点。如果第一次找到有同时包含两个节点的子树，则这棵子树的根就是LCA。也就是说，相当于下面的过程：

1.输入两个节点A和B

2.设当前节点为A

3.while dfs(当前节点)没有搜索到A和B

4.当前节点更新为当前节点的父节点

5.输出当前节点

很容易看出这个过程的正确性。首先，LCA的子树中必定有一个节点是A，一个是B，而且必定在两个节点到根节点的唯一路径上。

因此，我们可以引出定义：某两个节点的LCA就是其在DFS遍历整棵树时同时访问到这两个节点的“回溯最近节点”。而且，在刚刚遍历完这两个节点时，它们的LCA必定没有回溯！因此，我们就通过了时间戳做到了这一点。某两个节点的DFS间所访问到的哪些节点中的最小值必然是这两个节点的LCA。

【树上倍增（类似于二分步长）】

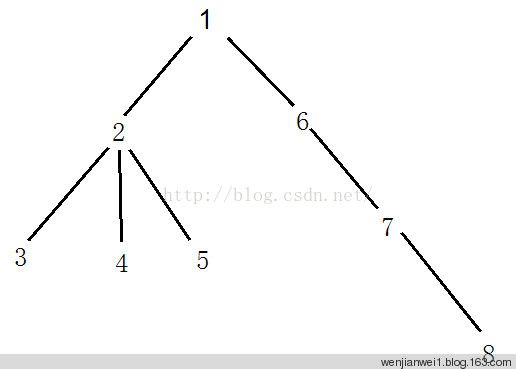
对于下面的这棵树，我们先随意指定一个编号：

  然后，我们对于每一个节点，记录其往上跳1个节点，2个节点，4个节点，8个节点，16个节点……2^k个节点所达到的节点编号。在这里，往上跳2^k个节点应达到的是节点-1，也就是说，向上跳2^k个节点是不可能的，但是跳2^(k-1)个节点应该可以跳到。这可以用链表存储，也可以直接开一个数组，以方便索引。

那么这个表怎样建立呢？难道对于每一个节点都要一直用while循环一直找到根节点吗？不是的，我们只需要稍加分析，就可以写出一种总时间复杂度O(Nlog2N)的优秀算法。

首先，每个点向上跳一个点，必定是其父节点，根节点就是-1。然后，显而易见的，向上跳2^i个节点，等价于先向上跳2^(i-1)个节点，再在向上跳的基础上再向上跳2^(i-1)个节点。当然，这要求向上跳到的节点的表已经算过了。于是，我们需要使用DFS，以保证这一次序。简单分析一下就可以得出最多往上跳log2N层，而一共有N个节点，乘在一块就是O(Nlog2N)。具体的实现如下：

1.DFS(根节点)，对于每个DFS到的节点（不包括回溯到的）：

2.设当前跳到的节点为DFS的目前节点的父节点

3.设当前向上跳2^i个节点，其中i=0

4.while 当前跳到的节点仍然存在（即不为-1）

5.当前节点的表中加入向上跳2^i跳到当前跳到的节点

6.++i

7.当前跳到的节点更新为当前跳到的节点向上跳2^(i-1)的节点

其实这一种算法相当于在树上添加了一些额外的边，有点像自动机的结构，就像AC自动机一样都和树（AC自动机实际上是添加了状态转移边的Trie树，或者说字典树）有关。我个人觉得这其实是一种双方向的状态转移，应该比较特殊。

回归正题，继续讲倍增算法。LCA不是每一次询问都要给两个点的编号吗？我们就设这两个点为点A和点B。首先，如果这两个点的深度不同（深度可以顺便在DFS时求出），则先将较深的一个节点向上一直跳，跳到和另一个点相同的深度，这可以用我们刚才所造的表，并用二进制的lowbit优化，实现如下：

1.设要向上跳k层，当前跳到节点为A'

2.while k != 0

3.A'向上跳lowbit(k)层

4.k -= lowbit(k)

接着相应的将相应的节点设为A’，如果A'和另一节点相同则LCA就是那个节点。于是，下面的思路就也很明朗了。二分LCA！比如说现在A和B在同一层上（深度相同），并且设深度都是100的话，就先向上跳64层，如果相同就只跳32层（在原来节点的基础上），不相同则再跳32层（在跳64层达到的两个节点的基础上），最后即可轻而易举地二分到答案了……这一过程似乎又称树上倍增算法，正确性的证明很简单，那个表的过程就不说了，而LCA的最终二分过程应该类似于二分步长，不断试探，最终必定能够找到答案。

最终的时间复杂度，由预处理和二分答案的过程可知，为O(Nlog2N+Qlog2N)，和RMQ相当。

【Tarjan算法：并查集的离线算法】

前两个算法，都是在线算法，都是可以在线处理询问的，但是在信息学竞赛中，因为是黑箱测试，我们也可以采取一种时间复杂度更为优秀的算法：Tarjan。这种算法是一种 离线的算法，要求事先给出每一个询问，而处理的时候不一定按问题的给出顺序回答。

Tarjan算法基于一个和RMQ那个章节中最后一部分所陈述的那些东西一样的事实。也就是说，当我们从根节点开始DFS时，我们在 刚刚好访问 完两个节点时，这两个节点的LCA 必定没有在DFS中回溯。

所以，我们设back[x]为点x回溯到的节点标号。初始时设back[x]=x，接着在DFS的过程中依次更新。

比如说，我们当前遍历完了点x的所有子树，那么我们就可以设定：back[x]=father[x]（father[x]表示x的父亲节点）。以此类推。

然后，我们将LCA每次询问的一个节点对称为一个问题，一个节点是某个问题的节点对两个节点中的一个，则称之为这一个节点涉及到了某个问题。当我们DFS到一个被某个（或者说某些，情况都是一样的）问题涉及的节点时，如果该问题的另外一个节点没有被访问，则什么都不做，如果曾被访问，则对当前节点x执行以下的操作（当然首先要设back[x]=father[x]）：  

while (x!=back[x]){

x = back[x];

}

最后得出来的x，就是LCA！于是将LCA相应地回答那个问题。那么，怎么用并查集呢？   注意到刚刚那段代码了没有，那段代码和并查集的代码是否有几分相似？所以，我们引入路径压缩！

int findLCA(int x){

if (x==back[x]) return x;

return x = findLCA(back[x]);

}

由并查集的时间复杂度可知，总的时间复杂度应该是O(N+Q* α(N) )。而且，这里的应用还不需要合并，只需要查询即可，写起来比普通的并查集还要简单。

【总结】

这三种方法，在信息学奥赛中，可谓是非常实用的算法。今年NOIP2015提高组的最后一题，就有这样的思想在里面。因此，在树与图这样的东西里，LCA几乎就是家常便饭了。所以，我们必须记住这些算法的原理和具体的实现。