Lecture 2 | 图像分类

本文是《CS231n: Convolutional Neural Networks for Visual Recognition》课程的学习笔记。
课程讲义：http://cs231n.stanford.edu/slides/2017/cs231n_2017_lecture2.pdf

知识点：

• 图像分类
• K-Nearest Neighbor 及其距离
• Linear classifiers

1 图像分类

图像分类是计算机视觉中最重要的一个任务，简单的说，就是给你一张包含某一特定物体的图像，让你识别出这个图像包含的物体是什么。
比如说，给了一张猫的照片，我们可以非常简单的识别出这是猫，这是因为我们的大脑做了非常多的关于这方面的学习。如果让电脑来识别这张图像，那就完全不一样了，因为电脑和我们看到的东西是完全不一样的，电脑看到的是记录着这张图像的所有的像素。

从计算机的角度，图像其实是一个个像素组成的，那么，即使仍然是一只猫的图像，由于下面情况的出现，会导致像素完全不同：

• 相机视角的变化
• 图像的光影变化
• 形态的变化
• 其他物体的遮挡
• 背景色的干扰
• 很多不同种类的猫

1.1 API

图像分类的API，可以用如下的代码表示：

def classify_image(image):
	# some classify code here (magic).
	return class_label

由于前面说到的在猫的识别上存在很多的问题，所以这里很难去定义一套算法来做识别。
为了解决这类问题，John Canny在1986年就通过检测特征点来提取猫的边缘的方式来完成猫的识别，这种方式对猫的识别可能有用，但是如果换了一种物体，则需要重新进行计算和检测了。

2 机器学习

那现在，我们可以通过数据驱动的方法（Data-Driven Approach）来完成相关的任务：

• 收集大量的数据集，包括训练图像和标注
• 通过机器学习来训练分类器

def train(images, labels):
	# Machine Learning
	return model

• 通过新的图像来评估分类器

def predict(model, test_images):
	# Use model to predict labels
	return test_labels

3 最邻近法

最邻近法在训练数据过程中只是单纯的把数据记录下来，在预测阶段则是将数据与训练数据进行对比来找出最相似的结果。
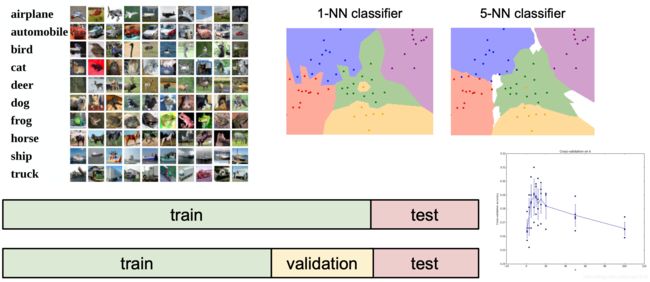
这里有一个比较好的训练数据叫做CIFAR10，包含10个分类，总共有5万张训练图像、1万张测试图像。

3.1 距离

在比较图像时，我们一般会用到两种距离：

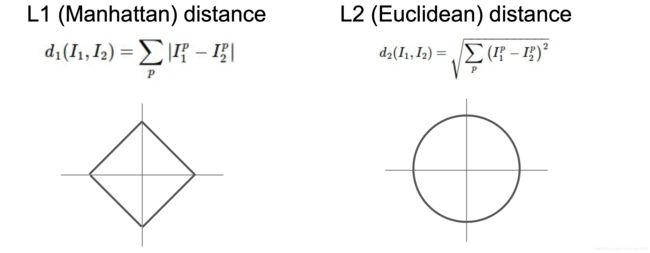
• L1 Distance (Manhattan Distance): $d1(I_1-I_2)=\sum (I_1^p-I_2^p)$。以点$O(0,0)$为中心，绘制与点$O(0,0)$的曼哈顿距离等于1的点的集合，最终得到的结果会是一个菱形，如下图左所示。
• L2 Distance (Euclidean Distance): $d2(I_1-I_2)=\sqrt{\sum (I_1^p-I_2^p{)}^2}$。以点$O(0,0)$为中心，绘制与点$O(0,0)$的欧几里得距离等于1的点的集合，最终得到的结果会是一个半径为1的圆，如下图右所示。
  
  对曼哈顿距离和欧氏距离，这里再多用一个图做一些说明：
  下图中红、黄、蓝分別表示所有曼哈顿距离都拥有一样的长度（12），而绿线表示的欧几里得距离有$6\ast \sqrt{2}\approx 8.48$的长度。

参考：

• 曼哈頓距離 - 维基百科，自由的百科全书
• The Square Circle, Exploiting Distance - Paul Bricman - Medium有比较详细的介绍

3.2 曼哈顿距离的KNN实现

下面以L1距离为例。
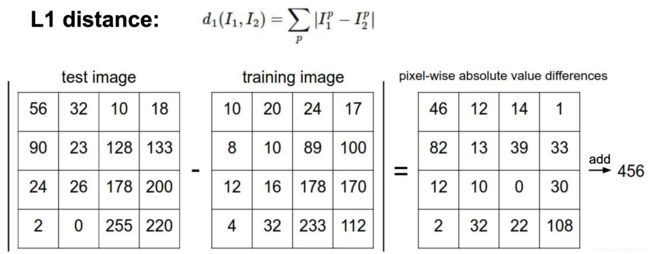
L1 Distance为 $d1(I_1-I_2)=\sum (I_1^p-I_2^p)$
即按照对应的像素来求差值的绝对值，最后所有的差值求和。

前面说过，训练数据阶段是读取并存储数据阶段，代码为：

def train(self, X, y):
	self.train_X = X
	self.train_y = y

预测阶段则是将数据与训练数据进行对比来找出最相似的结果，这里就需要用到L1 Distance了：

for i in xrange(num_test):
	distances = np.sum(np.abs(self.train_X - X[i, :]), axis=1)
	min_index = np.argmin(distances)
	y_predict[i] = self.train_y[min_indix]

3.3 KNN的复杂度

从最邻近算法可以看出，在训练阶段其时间复杂度为O(1)，但是在预测阶段其时间复杂度为O(N)，这种情况使得最邻近算法在现实生产中不可用，因为我们需要保证在用户能接触到的预测阶段的时间复杂度较低（运算较快）。
在后面要学到的卷积神经网络中，时间复杂度与最邻近法恰好相反，其是在训练阶段时间复杂度很大而在预测阶段很小。

除了从最邻近的点来做判断，也可以指定K参数，即从最邻近的K个点来做参考，也称为K邻近算法。
具体可以通过该Demo来查看http://vision.stanford.edu/teaching/cs231n-demos/knn/

3.4 超参数

从上面的例子中可以看到随着K和距离方式这两个参数的选取不同，最终得到的结果也不同，而这两个参数也称为「超参数」，即人为设定的参数，这些参数会随着问题的不同而选用不同的值，并且需要不断的尝试。

在设定最邻近值函数的超参数时，有几种设置训练数据的方式：

• 将所有的数据都作为训练数据来确定超参数。这种方式会使得该超参数对训练数据效果很好，出现过拟合的情况。
• 将数据集划分为训练数据和测试数据2类，将在测试数据上效果最好的参数设为超参数。这种方式也不太好，因为通过该方法得到的超参数不确定能在一个全新的数据中表现如何。
• 将数据集划分为训练数据、验证数据和测试数据3类，通过验证数据来获取最符合的超参数，通过测试数据来评估超参数的效果。这种方式是比较好且应用较为广泛的方式。
• 还有一种是将测试数据之外的数据集分为多份，以此将每份作为验证数据并以求均值的方式来得到超参数。这种方式对数据集较小的情况比较适用，但是在深度学习中很少使用。
  

总结一下，现实中基本不会使用K最邻近算法来做图像分类，主要是三个原因：

1. 在预测阶段太慢了
2. 通过像素之间的距离其实并不能提供有效的信息❓
3. 维度灾难。简单的说，就是维数增多会带来的高维空间数据稀疏化问题❓具体可以参考这篇文章《The Curse of Dimensionality in classification》或其某一中文翻译

关于第2、3点，我目前还不懂，还需要再做一些研究。

4 线性分类

线性分类(Linear Classifiers)是神经网络的基础，

线性分类是一种参数化的方法，输入图像x，然后应用参数（权重）w，经过一个函数计算，最后得到不同分类的得分（下图中是分为10类）。

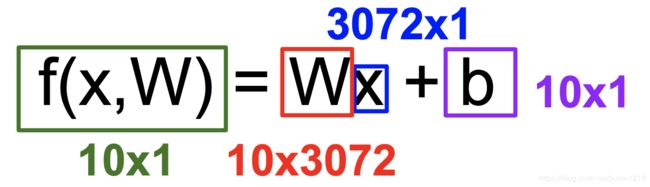
以CIFAR-10为例，线性分类主要是将输入数据的所有特征做一个平均，最终得到一个统一的模板来尝试识别不同的分类。所以得到的分类器不会太好。❓（这部分的理解也不好）

下图也列出来了一些线性分类处理不好的情况：

在通过线性分类得到不同分类的得分后，我们如何来判断这个W参数的效果呢？这就涉及到损失函数和优化了，后面章节再来探讨。