蓝桥杯第六届总决赛B组
1.积分之迷
小明开了个网上商店,卖风铃。共有3个品牌:A,B,C。为了促销,每件商品都会返固定的积分。
小明开业第一天收到了三笔订单:
第一笔:3个A + 7个B + 1个C,共返积分:315
第二笔:4个A + 10个B + 1个C,共返积分:420
第三笔:A + B + C,共返积分....
你能算出第三笔订单需要返积分多少吗?
答案:105
2.
完美正方形
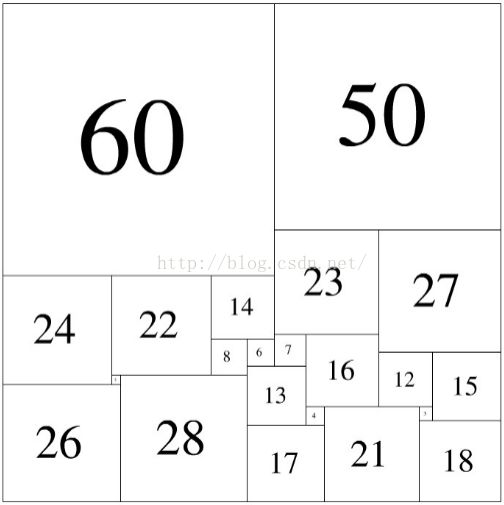
如果一些边长互不相同的正方形,可以恰好拼出一个更大的正方形,则称其为完美正方形。历史上,人们花了很久才找到了若干完美正方形。比如:如下边长的22个正方形
2 3 4 6 7 8 12 13 14 15 16 17 18 21 22 23 24 26 27 28 50 60
如【图1.png】那样组合,就是一种解法。此时,
紧贴上边沿的是:60 50
紧贴下边沿的是:26 28 17 21 18
22阶完美正方形一共有8种。下面的组合是另一种:
2 5 9 11 16 17 19 21 22 24 26 30 31 33 35 36 41 46 47 50 52 61
如果告诉你该方案紧贴着上边沿的是从左到右依次为:47 46 61,
你能计算出紧贴着下边沿的是哪几个正方形吗?
请提交紧贴着下边沿的正方形的边长,从左到右,用空格分开。
#include
using namespace std;
// 全局变量
namespace Global
{
const int MaxS = 46+47+61; // 正方形的边长
int All[] = {2,5,9,11,16,17,19,21,22,
24,26,30,31,33,35,36,41,50,52
};// 备选正方形边长
int Length = sizeof(All)/sizeof(All[0]);// 备选正方形的数量
int Square[MaxS][MaxS]= {0}; // 表示结果的完美正方形
}
// 线段树结点
struct TNode
{
int L, R; // [L, R]
int height; // 段高度( -1时表示该段不平滑,高度无意义 )
int inc; // 高度增量
// 计算宽度
inline int Width()const
{
return R-L+1;
}
// 计算中点
inline int Mid()const
{
return (L+R)>>1;
}
} NSet[1024];
inline int LSon( int i )
{
return i<<1;
}
inline int RSon( int i )
{
return LSon(i)+1;
}
inline int Parent( int i)
{
return i>>1;
}
// 建立线段树
void BuildTree( int i, int L, int R )
{
TNode* p = NSet+i;
p->L = L;
p->R = R;
p->height = 0;
p->inc = 0;
if( L < R )
{
int m = p->Mid();
BuildTree( LSon(i), L, m );
BuildTree( RSon(i), m+1, R);
}
}
// 增量的向下传递调整
// 注: NSet[i]必须为平滑区间
inline void Adjust( int i )
{
if( NSet[i].inc != 0 )
{
NSet[i].height += NSet[i].inc;
if( NSet[i].L != NSet[i].R )
{
NSet[LSon(i)].inc += NSet[i].inc;
NSet[RSon(i)].inc += NSet[i].inc;
}
NSet[i].inc = 0;
}
}
// 将区间[L,R]的高度统一增加(或减少)inc
// 注: 区间 [L, R] 必须平滑
void Add(int i, int L, int R, int inc )
{
TNode* p = NSet+i;
if( p->L == L && p->R == R )
{
// 操作后平滑性不变
p->inc += inc;
Adjust(i);
}
else
{
int m = p->Mid();
if( p->height != -1 ) // 表示该段本是平滑的
{
Adjust(i);
p->height = -1; // 现在开始该段不再平滑
}
int ls = LSon(i), rs = RSon(i);
if( R <= m )
Add( ls, L, R, inc );
else if( L > m )
Add( rs, L, R, inc );
else
{
Add( ls, L, m, inc );
Add( rs, m+1, R, inc );
}
// 平滑性恢复检验
if(NSet[ls].height != -1)
{
Adjust(ls);
if(NSet[rs].height != -1)
{
Adjust(rs);
if(NSet[ls].height == NSet[rs].height)
p->height = NSet[ls].height;
}
}
} // end else
}
// 获取最低段区间
void GetLowestInterval(int i, TNode* prev, TNode* lowest )
{
TNode* p = NSet+i;
if( p->height == -1 )
{
GetLowestInterval( LSon(i), prev, lowest );
GetLowestInterval( RSon(i), prev, lowest );
}
else
{
prev->R = p->R;
// 检验等高区间连续性
if( p->height != prev->height )
{
prev->L = p->L;
prev->height = p->height;
}
// 更新最低区间
if( prev->height <= lowest->height )
{
lowest->height = prev->height;
lowest->L = prev->L;
lowest->R = prev->R;
}
}
}
bool Dfs( int L, int R ,int H )
{
if( L > R )
{
TNode p, m;
m.height = 1000;
m.L = m.R = 1000;
p.height = 1000;
p.L = p.R = -1;
GetLowestInterval(1, &p, &m);
L = m.L;
R = m.R;
H = m.height;
}
int Width = R-L+1, temp=0;
if( Width == Global::MaxS && H != 0 ) return true;
for( int i = Global::Length; i-- > 0 ;)
{
temp = Global::All[i];
if( temp != 0 && temp <= Width )
{
Global::All[i] = 0;
Add( 1, L, L+temp-1, temp);
Global::Square[ H+temp-1 ][ L ] = temp;
if( Dfs( L+temp, R, H ) == true ) return true;
Add( 1, L, L+temp-1, -temp);
Global::All[i] = temp;
}
}
return false;
}
int main(int argc, char** argv)
{
BuildTree( 1, 0, Global::MaxS-1 );
Add( 1, 0, 46, 47);
Add( 1, 47, 92, 46);
Add( 1, 93, 153, 61);
if( Dfs( 1, 0, 0 ) )
{
for( int i = 0,t=0; i < Global::MaxS; i+=t)
{
t = Global::Square[ Global::MaxS-1 ][i];
cout << t << ' ';
}
}
return 0;
} 关联账户
为增大反腐力度,某地警方专门支队,对若干银行账户展开调查。如果两个账户间发生过转账,则认为有关联。如果a,b间有关联, b,c间有关联,则认为a,c间也有关联。
对于调查范围内的n个账户(编号0到n-1),警方已知道m条因转账引起的直接关联。
现在希望知道任意给定的两个账户,求出它们间是否有关联。有关联的输出1,没有关联输出0
小明给出了如下的解决方案:
#include
#define N 100
int connected(int* m, int p, int q)
{
return m[p]==m[q]? 1 : 0;
}
void link(int* m, int p, int q)
{
int i;
if(connected(m,p,q)) return;
int pID = m[p];
int qID = m[q];
for(i=0; i
4.密文搜索
福尔摩斯从X星收到一份资料,全部是小写字母组成。他的助手提供了另一份资料:许多长度为8的密码列表。
福尔摩斯发现,这些密码是被打乱后隐藏在先前那份资料中的。
请你编写一个程序,从第一份资料中搜索可能隐藏密码的位置。要考虑密码的所有排列可能性。
数据格式:
输入第一行:一个字符串s,全部由小写字母组成,长度小于1024*1024
紧接着一行是一个整数n,表示以下有n行密码,1<=n<=1000
紧接着是n行字符串,都是小写字母组成,长度都为8
要求输出:
一个整数, 表示每行密码的所有排列在s中匹配次数的总和。
例如:
用户输入:
aaaabbbbaabbcccc
2
aaaabbbb
abcabccc
则程序应该输出:
4
这是因为:第一个密码匹配了3次,第二个密码匹配了1次,一共4次。
资源约定:
峰值内存消耗 < 512M
CPU消耗 < 3000ms
请严格按要求输出,不要画蛇添足地打印类似:“请您输入...” 的多余内容。
所有代码放在同一个源文件中,调试通过后,拷贝提交该源码。
注意: main函数需要返回0
注意: 只使用ANSI C/ANSI C++ 标准,不要调用依赖于编译环境或操作系统的特殊函数。
注意: 所有依赖的函数必须明确地在源文件中 #include
提交时,注意选择所期望的编译器类型。
思路:因为要求每行密码的所有排列在s中匹配次数的总和,所以可以统计每行密码中所包含的各个字母的个数,然后选取主串中的长度为8的区间,比较是否与密码中包含的各个字母的个数相等。在选取主串中长度为8的区间时,实际上只有只有主串长度-7个长度为8的区间。
例如: 0 1 2 3 4 5 6 7 8 9 10 主串长度为11
则长度为8的区间只有0--7 1-- 8 2--9 3--10这4个,即11-4个。
#include
#include
#include
#include
#include
using namespace std;
int sum1[30],sum2[1000][30];
int sum=0, n;
int main (){
char ch1[1024*1024];
char ch2[10];
scanf("%s",ch1);
scanf("%d",&n);
memset(sum1,0,sizeof(sum1));
memset(sum2,0,sizeof(sum2));
for(int i=0;i<8;i++)
sum1[ ch1[i] -'a' ]++;
for(int i=0;i7){
sum1[ ch1[i-8]-'a' ]--;
sum1[ ch1[i]-'a' ]++;
}
for(int j=0;j 一个用素数解决的不错的方法
#include
#include
#include
#define maxn 1<<20+5
using namespace std;
char str[maxn],s[10];
int le[]={2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97,101,103,107};
long mul[maxn];
int main(){
int k=0;
char c;
mul[0]=1;
while(scanf("%c",&c)!=EOF){
if(c=='\n') break;
str[k++]=c;
mul[k]=mul[k-1]*le[c-'a'];
}
int n;
int res=0;
scanf("%d",&n);
getchar();
for(int i=0;i 5.居民集会
蓝桥村的居民都生活在一条公路的边上,公路的长度为L,每户家庭的位置都用这户家庭到公路的起点的距离来计算,第i户家庭距起点的距离为di。每年,蓝桥村都要举行一次集会。今年,由于村里的人口太多,村委会决定要在4个地方举行集会,其中3个位于公路中间,1个位最公路的终点。
已知每户家庭都会向着远离公路起点的方向去参加集会,参加集会的路程开销为家庭内的人数ti与距离的乘积。
给定每户家庭的位置di和人数ti,请为村委会寻找最好的集会举办地:p1, p2, p3, p4 (p1<=p2<=p3<=p4=L),使得村内所有人的路程开销和最小。
【输入格式】
输入的第一行包含两个整数n, L,分别表示蓝桥村的家庭数和公路长度。
接下来n行,每行两个整数di, ti,分别表示第i户家庭距离公路起点的距离和家庭中的人数。
【输出格式】
输出一行,包含一个整数,表示村内所有人路程的开销和。
【样例输入】
6 10
1 3
2 2
4 5
5 20
6 5
8 7
【样例输出】
18
【样例说明】
在距起点2, 5, 8, 10这4个地方集会,6个家庭需要的走的距离分别为1, 0, 1, 0, 2, 0,总的路程开销为1*3+0*2+1*5+0*20+2*5+0*7=18。
【数据规模与约定】
对于10%的评测数据,1<=n<=300。
对于30%的评测数据,1<=n<=2000,1<=L<=10000,0<=di<=L,di<=di+1,0<=ti<=20。
对于100%的评测数据,1<=n<=100000,1<=L<=1000000,0<=di<=L,di<=di+1,0<=ti<=1000000。
资源约定:
峰值内存消耗 < 512M
CPU消耗 < 5000ms
请严格按要求输出,不要画蛇添足地打印类似:“请您输入...” 的多余内容。
所有代码放在同一个源文件中,调试通过后,拷贝提交该源码。
注意: main函数需要返回0
注意: 只使用ANSI C/ANSI C++ 标准,不要调用依赖于编译环境或操作系统的特殊函数。
注意: 所有依赖的函数必须明确地在源文件中 #include
提交时,注意选择所期望的编译器类型。
dp[i][j]=min(dp[i-1][j]+sum[i-1][j]*(A[i]-A[i-1]),dp[i-1][j-1]);
#include
#include
#include
#include
#include
#include
#include
using namespace std;
#define INF 1.0e14;
const int maxn = 1e5+100;
typedef long long LL;
int A[maxn];
int B[maxn];
LL dp[maxn][4];
LL sum[maxn][4];
int main(){
int n,m;
scanf("%d%d",&n,&m);
int i,j,k;
for(i=1;i<=n;i++)
scanf("%d%d",&A[i],&B[i]);
for(i=1;i<=n;i++){
dp[i][0]=dp[i-1][0]+sum[i-1][0]*(A[i]-A[i-1]);
sum[i][0]=sum[i-1][0]+B[i];
for(j=1;j<=3;j++)
if(i==j){
dp[i][j]=dp[i-1][j-1];
sum[i][j]=B[i];
}
else if(i>j){
dp[i][j]=dp[i-1][j]+sum[i-1][j]*(A[i]-A[i-1]);
sum[i][j]=sum[i-1][j]+B[i];
if(dp[i][j]>=dp[i-1][j-1])
dp[i][j]=dp[i-1][j-1],sum[i][j]=B[i];
}
}
LL ans=dp[n][0];
if(n>1) ans=min(ans,dp[n][1]);
if(n>2) ans=min(ans,dp[n][2]);
if(n>3) ans=min(ans,dp[n][3]+sum[n][3]*(m-A[n]));
cout<
6.模型染色
在电影《超能陆战队》中,小宏可以使用他的微型机器人组合成各种各样的形状。现在他用他的微型机器人拼成了一个大玩具给小朋友们玩。为了更加美观,他决定给玩具染色。
小宏的玩具由n个球型的端点和m段连接这些端点之间的边组成。下图给出了一个由5个球型端点和4条边组成的玩具,看上去很像一个分子的球棍模型。
由于小宏的微型机器人很灵活,这些球型端点可以在空间中任意移动,同时连接相邻两个球型端点的边可以任意的伸缩,这样一个玩具可以变换出不同的形状。在变换的过程中,边不会增加,也不会减少。
小宏想给他的玩具染上不超过k种颜色,这样玩具看上去会不一样。如果通过变换可以使得玩具变成完全相同的颜色模式,则认为是本质相同的染色。现在小宏想知道,可能有多少种本质不同的染色。
【输入格式】
输入的第一行包含三个整数n, m, k,
分别表示小宏的玩具上的端点数、边数和小宏可能使用的颜色数。端点从1到n编号。
接下来m行每行两个整数a, b,表示第a个端点和第b个端点之间有一条边。输入保证不会出现两条相同的边。
【输出格式】
输出一行,表示本质不同的染色的方案数。由于方案数可能很多,请输入方案数除10007的余数。
【样例输入】
3 2 2
1 2
3 2
【样例输出】
6
【样例说明】
令(a, b, c)表示第一个端点染成a,第二个端点染成b,第三个端点染成c,则下面6种本质不同的染色:(1, 1, 1), (1, 1, 2), (1, 2, 1), (1, 2, 2), (2, 1, 2), (2, 2, 2)。
而(2, 1, 1)与(1, 1, 2)是本质相同的,(2, 2, 1)与(2, 1, 2)是本质相同的。
【数据规模与约定】
对于20%的评测数据,1<=n<=5, 1<=k<=2。
对于50%的评测数据,1<=n<=10, 1<=k<=8。
对于100%的评测数据,1<=n<=10, 1<=m<=45, 1<=k<=30。
资源约定:
峰值内存消耗 < 512M
CPU消耗 < 5000ms
请严格按要求输出,不要画蛇添足地打印类似:“请您输入...” 的多余内容。
所有代码放在同一个源文件中,调试通过后,拷贝提交该源码。
注意: main函数需要返回0
注意: 只使用ANSI C/ANSI C++ 标准,不要调用依赖于编译环境或操作系统的特殊函数。
注意: 所有依赖的函数必须明确地在源文件中 #include
提交时,注意选择所期望的编译器类型。