大顶堆的c++实现

Heap

定义

小顶堆：每个节点的值小于或等于孩子节点的值

堆在结构上符合完全二叉树的性质，存储上采用一维数组，利用下标来认亲。

可以使用优先队列实现大小顶堆

#include
#include
#include
	priority_queue, greater()> pq;  //小顶堆

构造

• 节点下沉,使得当前节点符合堆定义
  1. 当前节点与其左右孩子比较(考虑左右孩子只有一个)，取最小值放在根节点。
  2. 若发生交换，且交换子节点非叶，则继续下沉。
     

void sink(vector& v, int len, int root) {

		int minimum = root;
		int lchild = 2 * root + 1;  //从0开始存储
		int rchild = 2 * root + 2;

		if (lchild < len && v[lchild] < v[minimum])
			minimum = lchild;
		if (rchild < len && v[rchild] < v[minimum])
			minimum = rchild;

		if (root != minimum)  //叶子节点恒为假
		{
			swap(v[minimum], v[root]);
			sink(v, len, minimum);  //下沉到叶子节点结束
		}
	}

• 构建树的过程就是将所有非叶子节点调整为符合堆结构，最后一个非叶子节点是n/2-1;

	void buildMinHeap() {
		for (int i = vec.size() / 2 - 1; i >= 0; --i)  //对于每个非叶节点，下沉
			sink(vec, vec.size(), i);
	}

删除

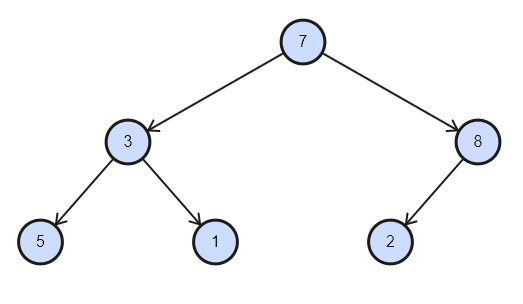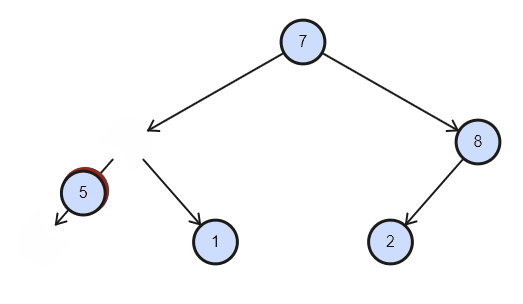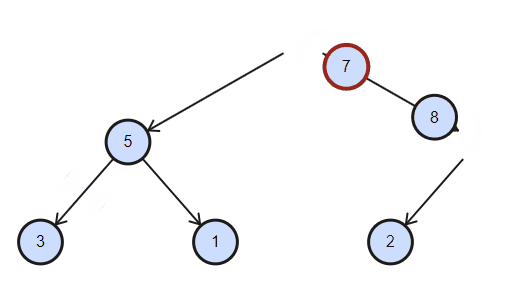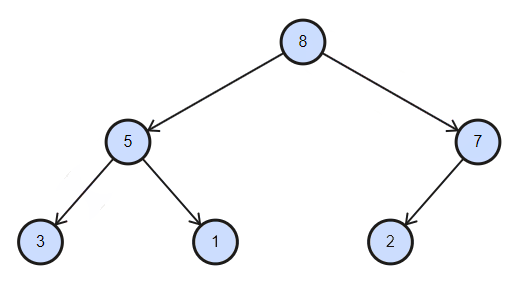
删除总是删除根节点，具体做法是将根节点与最后元素交换，删除最后元素，对根节点作下沉。(若实现任意位置的删除，需要下标合法性的额外检查)

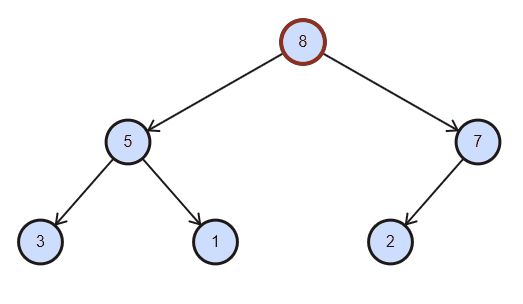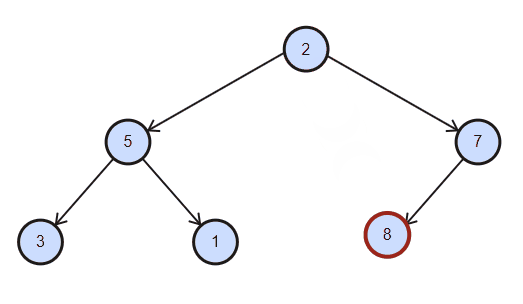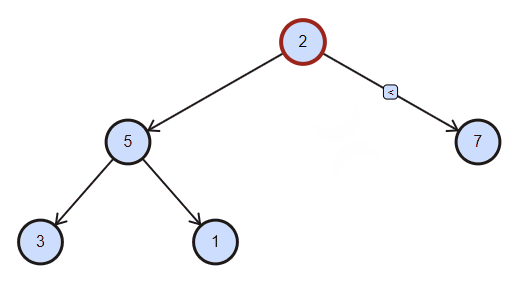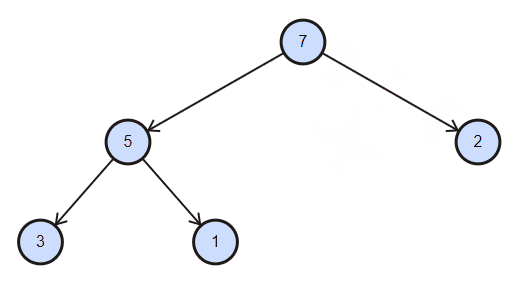
	void remove() {  
		swap(vec.front(), vec.back());
		vec.erase(vec.end()-1);
		sink(vec, vec.size(), 0);
	}

堆排序

堆排序的过程针对已经建立完成的堆，将最小值放在数组末尾，再把数组长度减一，作一次下沉操作就符合堆的结构特性。

	void heapSort() {
		for (int i = vec.size() - 1; i >= 0; --i) {
			swap(vec[0], vec[i]);  //最小值沉到排序序列的最后
			sink(vec, i, 0);  //再对前 n-1 个数排序
		}
	}

Question

为什么堆排序不稳定？

建堆的调整过程中，键值相同的两个记录相对位置会保持，此时是稳定的。在swap的时候，键值相同的记录在序列中的位置就有可能会改变。

测试用例

int main() {
	vector vec{ 7,3,8,5,1,2 };

	Heap heap(vec);
	heap.printHeap(heap.vec);
	heap.buildMinHeap();
	heap.printHeap(heap.vec);
	heap.remove();
	heap.printHeap(heap.vec);
	heap.heapSort();
	heap.printHeap(heap.vec);
}