主成分分析(PCA)与K-L变换
主成分分析与K-L变换
- 1. 主成分分析 —— 基于最大方差的描述
- 1.1 投影数据的方差
- 1.2 高维数据的降维
- 2. K-L变换 —— 基于最小误差的描述
- 2.1 内积空间中的正交变换
- 2.2 信号的正交分解
- 2.3 K-L变换
- 2.4 基于K-L变换的数据压缩
\qquad 主成分分析 ( P r i n c i p a l C o m p o n e n t A n a l y s i s , P C A ) (Principal\ Component\ Analysis,\ PCA) (Principal Component Analysis, PCA) 基于输入数据的协方差矩阵,可实现“去除数据集的相关性” —— 在数据处理中常用于通过“高维数据的降维”来实现特征提取,在信号处理中被称为 K K K- L L L 变换,常用于实现“数据压缩”。
这里的“相关性”是指数据集各维度之间的“线性”依赖关系,采用“协方差”来描述
以二维数据 x = ( x 1 , x 2 ) T \boldsymbol x=(x_1,x_2)^T x=(x1,x2)T 为例,“观测数据集不相关”是指协方差 c o v ( x 1 , x 2 ) = 0 cov(x_1,x_2)=0 cov(x1,x2)=0,即: x 1 x_1 x1 和 x 2 x_2 x2 两个分量不是线性相关的。此时,协方差矩阵为对角阵
详细内容可参考《协方差矩阵与二维高斯分布》
\qquad
1. 主成分分析 —— 基于最大方差的描述
\qquad 考虑观测数据集 { x i } i = 1 K ∈ R N \{\boldsymbol x_i\}_{i=1}^K\in R^N {xi}i=1K∈RN,将每个观测数据投影到某个单位方向 u ∈ R N , u T u = 1 \boldsymbol u\in R^N,\boldsymbol u^T\boldsymbol u=1 u∈RN,uTu=1。从数据处理的角度来看,如果观测数据集在单位方向 u \boldsymbol u u 上的投影值具有最大方差,那么方向 u \boldsymbol u u 就为主成分 ( P r i n c i p a l C o m p o n e n t ) (Principal\ Component) (Principal Component)。
1.1 投影数据的方差
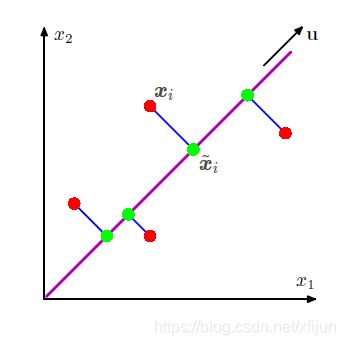
\qquad 如图 1 1 1 所示,(二维)数据集 { x i } i = 1 K \{\boldsymbol x_i\}_{i=1}^K {xi}i=1K (红色点)在投影之后,变成了单位方向 u \boldsymbol u u 上的向量集 { x ~ i } i = 1 K \{\tilde\boldsymbol x_i\}_{i=1}^K {x~i}i=1K(绿色点)。
图1 取自于《PRML》Fig 12.2
观测数据点 x i \boldsymbol x_i xi 经过投影之后为 x ~ i = ( u T x i ) u \tilde\boldsymbol x_i=(\boldsymbol u^T\boldsymbol x_i)\boldsymbol u x~i=(uTxi)u,即方向为 u \boldsymbol u u,长度为 u T x i \boldsymbol u^T\boldsymbol x_i uTxi
\qquad 投影后数据 { x ~ i } i = 1 K \{\tilde\boldsymbol x_i\}_{i=1}^K {x~i}i=1K (在 u \boldsymbol u u 方向上)的方差可定义为:
1 K ∑ i = 1 K { u T x i − u T x ˉ } 2 = u T S u \qquad\qquad\qquad\dfrac{1}{K}\displaystyle\sum_{i=1}^K\{\boldsymbol u^T\boldsymbol x_i-\boldsymbol u^T\bar\boldsymbol x\}^2=\boldsymbol u^TS\boldsymbol u K1i=1∑K{uTxi−uTxˉ}2=uTSu
\qquad\qquad 其中, x ˉ = 1 K ∑ i = 1 K x i \bar\boldsymbol x=\dfrac{1}{K}\displaystyle\sum_{i=1}^K\boldsymbol x_i xˉ=K1i=1∑Kxi 为观测数据集的样本均值
\qquad\qquad S = 1 K ∑ i = 1 K ( x i − x ˉ ) ( x i − x ˉ ) T S=\dfrac{1}{K}\displaystyle\sum_{i=1}^K(\boldsymbol x_i-\bar\boldsymbol x)(\boldsymbol x_i-\bar\boldsymbol x)^T S=K1i=1∑K(xi−xˉ)(xi−xˉ)T 为观测数据集的协方差矩阵
对于观测数据集 { x 1 , x 2 , ⋯ , x K } , ∀ x i ∈ R N \{\boldsymbol x_1,\boldsymbol x_2,\cdots,\boldsymbol x_K\},\ \forall \boldsymbol x_i\in R^N {x1,x2,⋯,xK}, ∀xi∈RN,记 x ˉ \bar\boldsymbol x xˉ 为数据集的样本均值
若将“去掉均值的数据集”写成矩阵形式,记为 X = [ x 1 − x ˉ , x 2 − x ˉ , ⋯ , x K − x ˉ ] N × K \bold X = [\boldsymbol x_1-\bar\boldsymbol x,\boldsymbol x_2-\bar\boldsymbol x,\cdots,\boldsymbol x_K-\bar\boldsymbol x]_{N\times K} X=[x1−xˉ,x2−xˉ,⋯,xK−xˉ]N×K
那么,数据集的协方差矩阵为: S = 1 K X T X S=\dfrac{1}{K}\bold X^T\bold X S=K1XTX
可参考《PCA图像压缩的matlab实现》
\qquad
\qquad 为了求使得方差 u T S u \boldsymbol u^TS\boldsymbol u uTSu 最大的 u \boldsymbol u u 方向,采用以下步骤:
( 1 ) \qquad(1) (1) 采用拉格朗日乘子法构造最优化问题:
max { u T S u + λ ( 1 − u T u ) } \qquad\qquad\qquad\qquad\max\ \{\ \boldsymbol u^TS\boldsymbol u+\lambda(1-\boldsymbol u^T\boldsymbol u)\ \} max { uTSu+λ(1−uTu) }
( 2 ) \qquad(2) (2) 令其对 u \boldsymbol u u 的偏导为 0 0 0,可得到:
S u = λ u \qquad\qquad\qquad\qquad S\boldsymbol u=\lambda\boldsymbol u Su=λu
\qquad 显然, u \boldsymbol u u 是协方差矩阵 S S S 的特征向量
\qquad λ \lambda λ 是 u \boldsymbol u u 所对应的特征值
( 3 ) \qquad(3) (3) 将等式两端左乘 u T \boldsymbol u^T uT,可得到:
u T S u = u T λ u = λ u T u = λ \qquad\qquad\qquad\qquad\boldsymbol u^TS\boldsymbol u=\boldsymbol u^T\lambda\boldsymbol u=\lambda\boldsymbol u^T\boldsymbol u=\lambda uTSu=uTλu=λuTu=λ
\qquad 这就说明,观测数据集在 S S S 的特征向量 u \boldsymbol u u 方向上投影后,“投影数据的方差值”正好等于对应的特征值 λ \lambda λ。
\qquad 如图 2 2 2 所示,若将协方差矩阵 S S S 的特征值按从大到小的顺序排列,最大特征值 λ 1 \lambda_1 λ1 所对应特征向量 u 1 \boldsymbol u_1 u1 的方向,即为第一主成分,该观测数据集“最主要的特征”体现在 u 1 \boldsymbol u_1 u1 方向上,投影后的数据在该方向上分布的散布程度最大; λ 2 \lambda_2 λ2 所对应特征向量 u 2 \boldsymbol u_2 u2 的方向,为第二主成分,“次主要的特征”体现在 u 2 \boldsymbol u_2 u2 方向上; ⋯ ⋯ \cdots\cdots ⋯⋯。
\qquad 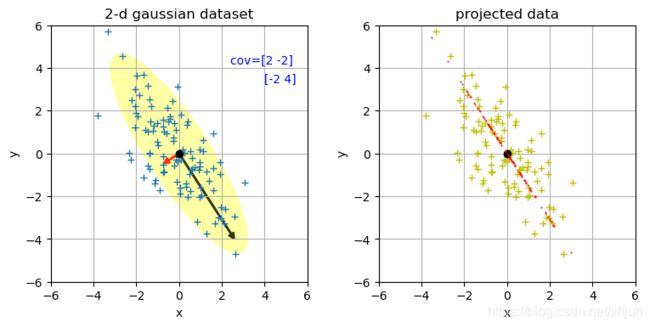
图2 从一个均值为 0 \boldsymbol 0 0,协方差矩阵为 [ 2 − 2 − 2 4 ] \left[\begin{matrix}2&-2\\-2&4\end{matrix}\right] [2−2−24] 的正态分布采样了 100 100 100 个数据(蓝色的 ‘+’ 号)组成观测数据集 { x i } i = 1 100 ∈ R 2 \{\boldsymbol x_i\}_{i=1}^{100}\in R^2 {xi}i=1100∈R2
通过对协方差矩阵进行特征分解,可求出:
( 1 ) (1) (1) 第一主成分为 u 1 = [ 0.5257 − 0.8507 ] \boldsymbol u_1=\left[\begin{matrix}0.5257\\-0.8507\end{matrix}\right] u1=[0.5257−0.8507](黑色箭头),观测数据集在该方向上的投影具有更大的方差
对应了协方差矩阵的最大特征值 λ 1 = 5.2360 \lambda_1=5.2360 λ1=5.2360
( 2 ) (2) (2) 第二主成分为 u 2 = [ − 0.8507 − 0.5257 ] \boldsymbol u_2=\left[\begin{matrix}-0.8507\\-0.5257\end{matrix}\right] u2=[−0.8507−0.5257](红色箭头),观测数据集在该方向上的投影具有更小的方差
对应了协方差矩阵较小的特征值 λ 2 = 0.7639 \lambda_2=0.7639 λ2=0.7639
由 100 100 100 个观测点计算得到的“观测数据集的协方差矩阵” S = [ 1.7809 − 1.7640 − 1.7640 3.6450 ] S=\left[\begin{matrix}1.7809&-1.7640\\-1.7640&3.6450\end{matrix}\right] S=[1.7809−1.7640−1.76403.6450],特征分解之后的两个主成分分别为:
( 1 ) (1) (1) 第一主成分为 u 1 ′ = [ 0.5162 − 0.8565 ] \boldsymbol u_1^{'}=\left[\begin{matrix}0.5162\\-0.8565\end{matrix}\right] u1′=[0.5162−0.8565],较大的特征值 λ 1 ′ = 4.7081 \lambda_1^{'}=4.7081 λ1′=4.7081(右图为投影数据)
可以看出,观测数据的主要变化特征( y y y 随 x x x 的线性变化)是沿着 u 1 ′ \boldsymbol u_1^{'} u1′ 方向(可参考《协方差矩阵与二维高斯分布》)
( 2 ) (2) (2) 第二主成分为 u 2 ′ = [ − 0.8565 − 0.5162 ] \boldsymbol u_2^{'}=\left[\begin{matrix}-0.8565\\-0.5162\end{matrix}\right] u2′=[−0.8565−0.5162],较小的特征值 λ 2 ′ = 0.7178 \lambda_2^{'}=0.7178 λ2′=0.7178
可以看出,即使只采样了 100 100 100 个数据,两组主成分的方向也是非常接近的
\qquad
1.2 高维数据的降维
\qquad 考虑 N N N 维观测数据集 { x i } i = 1 K \{\boldsymbol x_i\}_{i=1}^K {xi}i=1K,当 N N N 值比较大时,会极大增加运算量。例如,一幅 100 × 100 100\times 100 100×100 大小的图像实际上是 R 10000 R^{10000} R10000 空间中的一个元素( N = 10000 N=10000 N=10000)。
\qquad 然而,数据通常都是包含一些冗余的,“高维数据中的有效成分”实际上只包含在一个比较小的 M M M 维子空间( R M ⊂ R N , M < N R^M\sub R^N,\ M
\qquad 采用 P C A PCA PCA 提取出最重要的 M M M 个成分( 最大的 M M M 个特征值所对应的成分)组成 x ~ i ∈ R M \tilde\boldsymbol x_i\in R^M x~i∈RM 来表示完整的 N N N 维数据 x i ∈ R N \boldsymbol x_i\in R^N xi∈RN,从而实现了高维数据的降维。
\qquad
2. K-L变换 —— 基于最小误差的描述
\qquad 主成分分析,在信号处理领域也被称为 K K K- L L L 变换。也就是说,一个信号可以在 K K K- L L L 基上展开。
2.1 内积空间中的正交变换
\qquad 由线性代数理论可知,实对称矩阵 S N × N S_{N\times N} SN×N 可以通过一个正交矩阵 A A A 实现对角化(实对称矩阵的特征分解,可参考本文):
A S A − 1 = A S A T = [ λ 0 λ 1 ⋱ λ N − 1 ] \qquad\qquad ASA^{-1}=ASA^T=\left[\begin{matrix}\lambda_0&&&\\&\lambda_1&&\\&&\ddots&\\&&&\lambda_{N-1}\end{matrix}\right] ASA−1=ASAT=⎣⎢⎢⎡λ0λ1⋱λN−1⎦⎥⎥⎤
S p i = λ i p i ( i = 0 , 1 , ⋯ , N − 1 ) \qquad\qquad Sp_i=\lambda_ip_i\ \ (i=0,1,\cdots,N-1) Spi=λipi (i=0,1,⋯,N−1) 【 p i p_i pi 为特征值 λ i \lambda_i λi 所对应的特征向量】
\qquad\qquad 其中,正交矩阵 A = [ p 0 , p 1 , ⋯ , p N − 1 ] A=[p_0,p_1,\cdots,p_{N-1}] A=[p0,p1,⋯,pN−1] 满足 A − 1 = A T A^{-1}=A^T A−1=AT
\qquad 正交矩阵 A A A 的主要特点在于: A A A 中各列是两两正交的。
A − 1 = A T ⟹ A T A = I ⟹ { p i T p j = 0 , i ≠ j p i T p j = 1 , i = j \qquad\qquad A^{-1}=A^T\Longrightarrow A^TA=\bold I \ \Longrightarrow\left\{ \begin{aligned} \ p_i^Tp_j&=0&,i\neq j \\\\ p_i^Tp_j&=1&,i=j \end{aligned} \right. A−1=AT⟹ATA=I ⟹⎩⎪⎨⎪⎧ piTpjpiTpj=0=1,i=j,i=j
\qquad 若将正交矩阵 A A A 看成两个内积空间 X , Y X,Y X,Y 之间的线性变换,那么
A : X ⟶ Y \qquad\qquad\qquad A:X\longrightarrow Y A:X⟶Y
x ⟶ y = A x \qquad\qquad\qquad\qquad \boldsymbol x\longrightarrow \boldsymbol y=A\boldsymbol x x⟶y=Ax (正变换)
\qquad 正交变换可以保证信号在变换前后的能量保持不变,即: ∥ x ∥ X = ∥ y ∥ Y = ∥ A x ∥ Y \Vert \boldsymbol x\Vert_X=\Vert \boldsymbol y\Vert_Y=\Vert A\boldsymbol x\Vert_Y ∥x∥X=∥y∥Y=∥Ax∥Y
\qquad
2.2 信号的正交分解
\qquad 由于正交矩阵 A A A 中的各列两两正交, A A A 中的列构成了空间的一组“正交规范基”,若认为 y = A x \boldsymbol y=A\boldsymbol x y=Ax 为正变换,反变换也必然存在,即:
x = A − 1 y = A T y \qquad\qquad\qquad\boldsymbol x=A^{-1}\boldsymbol y=A^T\boldsymbol y x=A−1y=ATy (逆变换)
\qquad 上述逆变换意味着,一个信号 x = [ x 0 , x 1 , ⋯ , x N − 1 ] T \boldsymbol x=[x_0,x_1,\cdots,x_{N-1}]^T x=[x0,x1,⋯,xN−1]T 可以在一组正交基 { φ ( ⋅ , n ) } \{\varphi(\cdot,n)\} {φ(⋅,n)} 上展开,展开系数为 y = [ y 0 , y 1 , ⋯ , y N − 1 ] T \boldsymbol y=[y_0,y_1,\cdots,y_{N-1}]^T y=[y0,y1,⋯,yN−1]T,也就是:
x i = ∑ n = 0 N − 1 y n φ ( i , n ) \qquad\qquad\qquad x_i=\displaystyle\sum_{n=0}^{N-1}y_n\varphi(i,n) xi=n=0∑N−1ynφ(i,n), 其中 φ ( i , n ) \varphi(i,n) φ(i,n) 为变换核
逆变换矩阵 A T = [ φ ( 0 , 0 ) ⋯ φ ( 0 , n ) ⋯ φ ( 0 , N − 1 ) ⋮ ⋮ ⋮ φ ( i , 0 ) ⋯ φ ( i , n ) ⋯ φ ( i , N − 1 ) ⋮ ⋮ ⋮ φ ( N − 1 , 0 ) ⋯ φ ( N − 1 , n ) ⋯ φ ( N − 1 , N − 1 ) ] A^T=\left[\begin{matrix}\varphi(0,0)&\cdots&\varphi(0,n)&\cdots&\varphi(0,N-1)\\ \vdots&&\vdots&&\vdots \\ \varphi(i,0)&\cdots&\varphi(i,n)&\cdots&\varphi(i,N-1)\\ \vdots&&\vdots&&\vdots \\ \varphi(N-1,0)&\cdots&\varphi(N-1,n)&\cdots&\varphi(N-1,N-1)\end{matrix}\right] AT=⎣⎢⎢⎢⎢⎢⎢⎡φ(0,0)⋮φ(i,0)⋮φ(N−1,0)⋯⋯⋯φ(0,n)⋮φ(i,n)⋮φ(N−1,n)⋯⋯⋯φ(0,N−1)⋮φ(i,N−1)⋮φ(N−1,N−1)⎦⎥⎥⎥⎥⎥⎥⎤
\qquad 例如,一维离散傅里叶变换的逆变换核为 φ ( i , n ) = e j 2 π i n N \varphi(i,n)=e^{j\frac{2\pi in}{N}} φ(i,n)=ejN2πin,那么
y = A x ⟶ y n = ∑ i = 0 N − 1 x i e − j 2 π i n N , n = 0 , 1 , ⋯ , N − 1 \qquad\qquad\boldsymbol y= A\boldsymbol x\ \ \longrightarrow y_n=\displaystyle\sum_{i=0}^{N-1}x_ie^{-j\frac{2\pi in}{N}},\qquad\ \ \ n=0,1,\cdots,N-1 y=Ax ⟶yn=i=0∑N−1xie−jN2πin, n=0,1,⋯,N−1
x = A T y ⟶ x i = 1 N ∑ n = 0 N − 1 y n e j 2 π i n N , i = 0 , 1 , ⋯ , N − 1 \qquad\qquad\boldsymbol x= A^T\boldsymbol y\longrightarrow x_i=\dfrac{1}{N}\displaystyle\sum_{n=0}^{N-1}y_ne^{j\frac{2\pi in}{N}},\qquad i=0,1,\cdots,N-1 x=ATy⟶xi=N1n=0∑N−1ynejN2πin,i=0,1,⋯,N−1
可以验证一维离散傅里叶逆变换 A T = [ e j 2 π i n N ] A^T=[e^{j\frac{2\pi in}{N}}] AT=[ejN2πin] 为正交矩阵
\qquad
2.3 K-L变换
\qquad 对于一个宽平稳的随机向量 x = [ x 0 , x 1 , ⋯ , x N − 1 ] T \boldsymbol x=[x_0,x_1,\cdots,x_{N-1}]^T x=[x0,x1,⋯,xN−1]T,其协方差矩阵为 S x = E [ ( x − μ x ) ( x − μ x ) T ] S_{\boldsymbol x}=E[(\boldsymbol x-\boldsymbol\mu_{\boldsymbol x})(\boldsymbol x-\boldsymbol\mu_{\boldsymbol x})^T] Sx=E[(x−μx)(x−μx)T],其中 μ x = E [ x ] \boldsymbol\mu_{\boldsymbol x}=E[\boldsymbol x] μx=E[x]。
K \qquad K K- L L L 变换记为 y = A x \boldsymbol y= A\boldsymbol x y=Ax —— 寻找正交矩阵 A A A 将输入信号 x \boldsymbol x x 变换为输出信号 y \boldsymbol y y(变换域),同时使得随机变量 y \boldsymbol y y 的协方差矩阵 S y S_{\boldsymbol y} Sy 为对角阵,即:
S y = A S x A T = [ λ 0 λ 1 ⋱ λ N − 1 ] \qquad\qquad S_{\boldsymbol y}=AS_{\boldsymbol x}A^T=\left[\begin{matrix}\lambda_0&&&\\&\lambda_1&&\\&&\ddots&\\&&&\lambda_{N-1}\end{matrix}\right] Sy=ASxAT=⎣⎢⎢⎡λ0λ1⋱λN−1⎦⎥⎥⎤
\qquad 由于随机变量 y \boldsymbol y y 的协方差矩阵 S y S_{\boldsymbol y} Sy 为对角阵,各分量之间的协方差均为零,原始信号 x \boldsymbol x x 经过 y = A x \boldsymbol y= A\boldsymbol x y=Ax 变换后,完全去除了相关性。
\qquad 
以图像块为例:
(1) 图像像素在空间域中相关性很强(局部区域像素通常比较接近),能量分布比较均匀
(2) 图像块经过正交变换(坐标旋转或变换)后,能量集中在少数坐标轴上,变换系数 { y n } \{y_n\} {yn}之间的相关性近似统计独立
(3) 图像块的能量在变换域中的分布相对集中(集中在直流和少数低频系数),可采用较少的编码比特表示,达到压缩编码的目的
\qquad 在 K K K- L L L 基 { ϕ 0 , ϕ 1 , ⋯ , ϕ N − 1 } \{\phi_0,\phi_1,\cdots,\phi_{N-1}\} {ϕ0,ϕ1,⋯,ϕN−1} 上可以将输入信号 x \boldsymbol x x 在变换域展开:
x = A T y = [ ϕ 0 , ϕ 1 , ⋯ , ϕ N − 1 ] y = ∑ n = 0 N − 1 y n ϕ n \qquad\qquad\boldsymbol x=A^T\boldsymbol y=[\phi_0,\phi_1,\cdots,\phi_{N-1}]\boldsymbol y=\displaystyle\sum_{n=0}^{N-1}y_n\phi_n x=ATy=[ϕ0,ϕ1,⋯,ϕN−1]y=n=0∑N−1ynϕn
\qquad\qquad 其中, y n = ⟨ x , ϕ n ⟩ = x T ϕ n y_n=\langle\boldsymbol x, \phi_n\rangle=\boldsymbol x^T\phi_n yn=⟨x,ϕn⟩=xTϕn 是 x \boldsymbol x x 在 ϕ n \phi_n ϕn 上的投影
\qquad 因此
x = A T y = ∑ n = 0 N − 1 ⟨ x , ϕ n ⟩ ϕ n \qquad\qquad\boldsymbol x=A^T\boldsymbol y=\displaystyle\sum_{n=0}^{N-1}\langle\boldsymbol x, \phi_n\rangle\phi_n x=ATy=n=0∑N−1⟨x,ϕn⟩ϕn
由 A T = A − 1 ⟹ A T A = I A^T=A^{-1}\Longrightarrow A^TA=\bold I AT=A−1⟹ATA=I,说明 A A A 中各列 { p i } \{p_i\} {pi} 两两正交
又由于 A T = A − 1 ⟹ A A T = I ⟹ ( A T ) T ( A T ) = I A^T=A^{-1}\Longrightarrow AA^T=\bold I\Longrightarrow(A^T)^T(A^T)=\bold I AT=A−1⟹AAT=I⟹(AT)T(AT)=I,说明 A T A^T AT 中各列 { ϕ n } \{\phi_n\} {ϕn} 也两两正交
\qquad
2.4 基于K-L变换的数据压缩
\qquad 要对信号 x \boldsymbol x x 做数据压缩,只要舍去变换系数 y \boldsymbol y y 的一些系数。假设只保留 M < N M
x ^ = ∑ n = 0 M − 1 y n ϕ n = ∑ n = 0 N − 1 ⟨ x , ϕ n ⟩ ϕ n \qquad\qquad\hat\boldsymbol x=\displaystyle\sum_{n=0}^{M-1}y_n\phi_n=\displaystyle\sum_{n=0}^{N-1}\langle\boldsymbol x, \phi_n\rangle\phi_n x^=n=0∑M−1ynϕn=n=0∑N−1⟨x,ϕn⟩ϕn
\qquad 压缩后数据 x ^ \hat\boldsymbol x x^ 对原始数据 x \boldsymbol x x 的均方误差为: ε = E [ ( x ^ − x ) 2 ] \varepsilon=E[(\hat\boldsymbol x-\boldsymbol x)^2] ε=E[(x^−x)2]
\qquad 因此, K K K- L L L 变换也可以理解为:在保留 M M M 个系数的前提下,为了获得最大压缩率,选择一组标准正交基 { ϕ 0 , ϕ 1 , ⋯ , ϕ N − 1 } \{\phi_0,\phi_1,\cdots,\phi_{N-1}\} {ϕ0,ϕ1,⋯,ϕN−1},使得上述均方误差最小。
ε = E [ ( x ^ − x ) 2 ] = E { [ ∑ n = M N − 1 y n ϕ n ] 2 } = E { ⟨ ∑ n = M N − 1 y n ϕ n , ∑ n = M N − 1 y n ϕ n ⟩ } , ⟨ ϕ i , ϕ j ⟩ = 0 ( i ≠ j ) = E { ∑ n = M N − 1 y n 2 } , ⟨ ϕ n , ϕ n ⟩ = 1 = E { ∑ n = M N − 1 [ x T ϕ n ] 2 } , [ x T ϕ n ] 2 = ( x T ϕ n ) T ( x T ϕ n ) = E { ∑ n = M N − 1 [ ϕ n T x x T ϕ n ] } = ∑ n = M N − 1 ϕ n T E { x x T } ϕ n \qquad\qquad\begin{aligned}\varepsilon&=E[(\hat\boldsymbol x-\boldsymbol x)^2]=E\left\{\left[\displaystyle\sum_{n=M}^{N-1}y_n\phi_n \right]^2 \right\} \\ &=E\left\{ \langle \displaystyle\sum_{n=M}^{N-1}y_n\phi_n,\displaystyle\sum_{n=M}^{N-1}y_n\phi_n \rangle \right\},\quad \langle\phi_i,\phi_j\rangle=0(i\neq j) \\ &=E\left\{\displaystyle\sum_{n=M}^{N-1}y_n^2 \right\},\qquad\qquad\qquad\quad \langle\phi_n,\phi_n\rangle=1\\ &=E\left\{\displaystyle\sum_{n=M}^{N-1}[\boldsymbol x^T\phi_n]^2 \right\},\qquad\qquad\quad [\boldsymbol x^T\phi_n]^2=(\boldsymbol x^T\phi_n)^T(\boldsymbol x^T\phi_n) \\ &=E\left\{\displaystyle\sum_{n=M}^{N-1}[\phi_n^T\boldsymbol x\boldsymbol x^T\phi_n] \right\} \\ &=\displaystyle\sum_{n=M}^{N-1}\phi_n^TE\left\{\boldsymbol x\boldsymbol x^T\right\}\phi_n \end{aligned} ε=E[(x^−x)2]=E⎩⎨⎧[n=M∑N−1ynϕn]2⎭⎬⎫=E{⟨n=M∑N−1ynϕn,n=M∑N−1ynϕn⟩},⟨ϕi,ϕj⟩=0(i=j)=E{n=M∑N−1yn2},⟨ϕn,ϕn⟩=1=E{n=M∑N−1[xTϕn]2},[xTϕn]2=(xTϕn)T(xTϕn)=E{n=M∑N−1[ϕnTxxTϕn]}=n=M∑N−1ϕnTE{xxT}ϕn
\qquad 假设 x \boldsymbol x x 已去除均值,那么 E { x x T } = S x E\left\{\boldsymbol x\boldsymbol x^T\right\}=S_{\boldsymbol x} E{xxT}=Sx,那么最小均方误差: ε = ∑ n = M N − 1 ϕ n T S x ϕ n \varepsilon=\displaystyle\sum_{n=M}^{N-1}\phi_n^TS_{\boldsymbol x}\phi_n ε=n=M∑N−1ϕnTSxϕn
\qquad 同样采用拉格朗日乘子法构造出最优化问题:
min { ε + λ ( 1 − ϕ T ϕ ) } \qquad\qquad\qquad\min\ \{\ \varepsilon+\lambda(1-\phi^T\phi)\ \} min { ε+λ(1−ϕTϕ) }
\qquad 对 ϕ n \phi_n ϕn求偏导:
∂ ∂ ϕ n { ε + λ ( 1 − ϕ T ϕ ) } = 0 \qquad\qquad\qquad\dfrac{\partial}{\partial \phi_n}\{\ \varepsilon+\lambda(1-\phi^T\phi)\ \}=0 ∂ϕn∂{ ε+λ(1−ϕTϕ) }=0
\qquad 可求得:
S x ϕ n = λ n ϕ n , n = M , ⋯ , N − 1 \qquad\qquad\qquad S_{\boldsymbol x}\phi_n=\lambda_n\phi_n,\quad n=M,\cdots,N-1 Sxϕn=λnϕn,n=M,⋯,N−1
\qquad
\qquad 因此,在变换域截短数据后的均方误差为:
ε = ∑ n = M N − 1 ϕ n T S x ϕ n = ∑ n = M N − 1 ϕ n T λ n ϕ n = ∑ n = M N − 1 λ n \qquad\qquad\qquad\varepsilon=\displaystyle\sum_{n=M}^{N-1}\phi_n^TS_{\boldsymbol x}\phi_n=\displaystyle\sum_{n=M}^{N-1}\phi_n^T\lambda_n\phi_n=\displaystyle\sum_{n=M}^{N-1}\lambda_n ε=n=M∑N−1ϕnTSxϕn=n=M∑N−1ϕnTλnϕn=n=M∑N−1λn
\qquad 为了使均方误差最小,将协方差矩阵 S x S_{\boldsymbol x} Sx 的特征值按照从大到小的顺序排列,即 λ 0 ≥ λ 1 ≥ ⋯ ≥ λ N − 1 \lambda_0\geq\lambda_1\geq\cdots\geq\lambda_{N-1} λ0≥λ1≥⋯≥λN−1,保留最大的 M M M 个特征值,相当于在变换域(保留 M M M个变换系数时)保留了信号的最大能量。
\qquad
\qquad 由于 K − L K-L K−L变换能够完全去除原始信号 x \boldsymbol x x 的相关性,通过保留最大的 M M M 个特征值来进行数据压缩时可以实现截短后数据 x ^ \hat\boldsymbol x x^ 的均方误差最小, K − L K-L K−L变换也被称为“最佳变换”。然而,由于 K − L K-L K−L变换的基取决于协方差矩阵 S x S_{\boldsymbol x} Sx,协方差矩阵的特征值和特征向量的计算没有像 F F T FFT FFT 之类的快速算法,限制了其应用场景。离散余弦变换 D C T DCT DCT 在满足一阶马尔可夫过程假设的前提下,可以极好地近似 K − L K-L K−L变换,又有快速算法,因而在压缩编码中得到了广泛应用。
\qquad
代码实现:PCA图像压缩
实现原理:
(1)将 M × N M\times N M×N 大小的图像进行分块,若每个图像块大小为 B s × B s B_s\times B_s Bs×Bs,整幅图像包含了 N s N_s Ns 个图像块,也就是满足 M N = N s B s 2 MN=N_sB_s^2 MN=NsBs2
(2)相当于构建了一个 B s 2 × 1 B_s^2\times 1 Bs2×1 的随机向量,整幅图像包含了该随机向量的 N s N_s Ns 次实现
(3)PCA 针对该随机向量的 N s N_s Ns 次实现来展开,寻找该随机向量的 B s 2 B_s^2 Bs2 个分量中最重要的 p p p 个主分量
【从K-L变换的角度来看】:一个 B s 2 × 1 B_s^2\times 1 Bs2×1 输入图像数据,经过K-L变换后,在新的 B s 2 B_s^2 Bs2 维空间中仅保留 p p p 个维度(其实就是降维),若采用 PCA 选中的这 p p p 个维度来表示图像,可以使得“变换后图像数据”的能量达到最大。
(4)从K-L变换域回到原始图像的空间域,只需要在 B s 2 B_s^2 Bs2 维变换域空间中保留 p p p 个维度的分量值,将剩余的 B s 2 − p B_s^2-p Bs2−p 个分量置 0 0 0。
上述过程仅仅考虑了图像压缩在变换域的表现,并未考虑其他的量化、编码等过程。