奇异值分解(SVD)摘记——从EVD到SVD

1. 矩阵的对角化(Diagonalization)

\qquad 假设 $A_{n\times n}$ 具有 $n$ 个线性无关的特征向量 $\{x_1,x_2,\cdots ,x_n\},x_i\in R^n$，可以定义特征向量矩阵 $S=[x_1,x_2,\cdots ,x_n]$，那么矩阵 $A$ 可以被对角化 $(diagonalized)$ 为一个对角阵 $\Lambda$（对角线元素为特征值）：

$S^{-1}AS=\Lambda =\left[\begin{array}{cccc}{\lambda }_1& & & \\ & {\lambda }_2& & \\ & & \ddots & \\ & & & {\lambda }_n\end{array}\right]$　　或者　　$A=S\Lambda S^{-1}$

\qquad 为了完成矩阵 $A$ 的对角化，其特征向量矩阵 $S$ 必须可逆（要求 $n$ 个线性无关的特征向量，或者没有重复的特征值）。

\qquad 上述对角化的过程实际上是：

\qquad\qquad 由：　$A{x}_i={\lambda }_i{x}_i,i=1,\cdots ,n$

\qquad\qquad 可得：$AS=A[x_1,x_2,\cdots ,x_n]=[{\lambda }_1{x}_1,{\lambda }_2{x}_2,\cdots ,{\lambda }_n{x}_n]$

\qquad\qquad 而：　$[{\lambda }_1{x}_1,{\lambda }_2{x}_2,\cdots ,{\lambda }_n{x}_n]=[x_1,x_2,\cdots ,x_n]\left[\begin{array}{cccc}{\lambda }_1& & & \\ & {\lambda }_2& & \\ & & \ddots & \\ & & & {\lambda }_n\end{array}\right]=S\Lambda$

\qquad 矩阵的对角化可以简化很多问题。例如，$A^m=\underset{m}{S\Lambda S^{-1}S\Lambda S^{-1}\cdots S\Lambda S^{-1}}=S{\Lambda }^m{S}^{-1}$
\qquad

2. 实对称矩阵的特征分解(Eigenvalue Decomposition,EVD)

2.1 实对称矩阵的对角化

\qquad 假设 $A_{n\times n}$ 为实对称$\text{(}realsymmetric)$矩阵，考虑其对角化过程：
\qquad
$\{\begin{array}{rl}A& =S\Lambda S^{-1}\\ A& =A^T\end{array}$ $⟹$　$A^T={\left(S\Lambda S^{-1}\right)}^T={\left(S^{-1}\right)}^T\Lambda S^T$

$⟹$　$A=S\Lambda S^{-1}={\left(S^{-1}\right)}^T\Lambda S^T=A^T$

$⟹$　$S^{-1}=S^T$ 或 $S^{T}S=\mathbf{I}$
\qquad
\qquad 此时，特征向量矩阵 $S=[x_1,x_2,\cdots ,x_n],x_i\in R^n$ 是正交矩阵 $(orthogonalmatrix)$，具有特殊的性质：$S$ 中任意一个特征向量 $x_i$ 与其他特征向量 $x_j,(j\ne i)$ 都正交。

$S^{T}S=\mathbf{I}⟹\{\begin{array}{rlr}{x}_i^T{x}_j& =0& ,i\ne j\\ x_i^T{x}_j& =1& ,i=j\end{array}$

\qquad 为了区别于一般矩阵的对角化，记实对称矩阵的正交矩阵（特征向量矩阵）为 $V$、特征值对角阵为 $D$，那么实对称矩阵 $A$ 可以对角化为：

$A=VD{V}^{-1}=VD{V}^T$，　其中 $V^{T}V=\mathbf{I}$ 或 $V^{-1}=V^T$
\qquad

2.2 正交矩阵的几何意义

\qquad 在实对称矩阵 $A=VD{V}^{-1}$ 的对角化过程中，正交矩阵 $V$ 的主要作用在于：

• 将实对称矩阵 $A$ 看成 $R^n$ 到 $R^n$ 的线性变换

$A:R^n⟶R^n$
$v_i⟶A{v}_i,v_i,A{v}_i\in R^n$

• 实对称矩阵 $A$ 的特征向量矩阵 $V$ 提供了变换前后的 $R^n$ 中的正交基 $\{v_1,v_2,\cdots ,v_n\}$

\qquad 将 $A$ 的对角化写为 $AV=VD$，也就是 $A{v}_i={\lambda }_i{v}_i$$,v_i\in R^n$，那么：
$(1)$ 向量 $v_i\in R^n$ 经过矩阵 $A$ 变换之后仍在 $R^n$ 中 $(thetransformationtakes{R}^{n}toitself)$
$(2)$ 向量 $v_i$ 的方向没变，只是向量的长度以 ${\lambda }_i$ 的比率进行了缩放
\qquad
\qquad 因此，如果采用正交矩阵 $V$ 中的特征向量 $\{v_1,v_2,\cdots ,v_n\},v_i\in R^n$ 同时作为构建变换前的 $R^n$ 和变换后的 $R^n$ 的基向量，那么变换前后的 $R^n$ 仅仅在尺度上发生了改变（如图 $1$ 和图 $3$ 所示）。

\qquad
例1　　实对称矩阵 $A=\left[\begin{array}{cc}3& 0\\ 0& 1\end{array}\right]$，对应了 $R^2$ 中的线性变换：$\left[\begin{array}{cc}3& 0\\ 0& 1\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]=\left[\begin{array}{c}3x_1\\ x_2\end{array}\right],\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]\in R^2$

\qquad 　　 特征向量为 ${\mathbf{v}}_1=\left[\begin{array}{c}1\\ 0\end{array}\right]$ 和 ${\mathbf{v}}_2=\left[\begin{array}{c}0\\ 1\end{array}\right]$，特征向量矩阵 $V=\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]$

\qquad 　　 特征值为 ${\lambda }_1=3,{\lambda }_2=1$，特征值对角阵 $D=\left[\begin{array}{cc}3& 0\\ 0& 1\end{array}\right]$
\qquad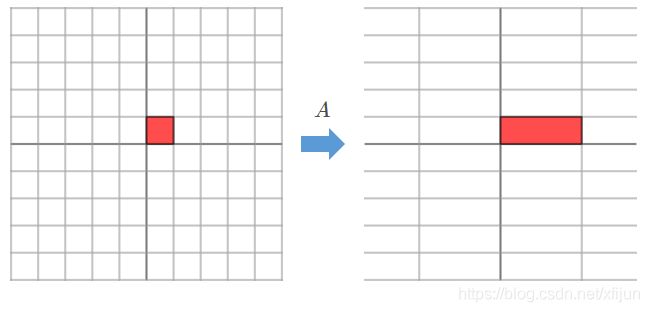

图1 标准坐标轴方向正好是特征向量的方向：${\mathbf{e}}_1=[1,0{]}^T={\mathbf{v}}_1,{\mathbf{e}}_2=[0,1{]}^T={\mathbf{v}}_2$
由 $A{v}_i={\lambda }_i{v}_i$，特征向量 ${\mathbf{v}}_i$ 经过线性变换之后，在新的 $R^2$ 中方向不会改变，只是改变了长度。
因此，对于“标准坐标轴方向”的单位向量 ${\mathbf{e}}_1$ 和 ${\mathbf{e}}_2$ 而言，在新的 $R^2$ 中方向仍保持不变：
$(1){\mathbf{e}}_1$ 方向上的尺度放大了 ${\lambda }_1=3$ 倍
$(2){\mathbf{e}}_2$ 方向上的尺度放大了 ${\lambda }_2=1$ 倍（尺度没变）

例2　　实对称矩阵 $A=\left[\begin{array}{cc}2& 1\\ 1& 2\end{array}\right]$，对应了 $R^2$ 中的线性变换：$\left[\begin{array}{cc}2& 1\\ 1& 2\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]=\left[\begin{array}{c}2x_1+x_2\\ x_1+2x_2\end{array}\right]$

\qquad 　　 特征向量为 ${\mathbf{v}}_1=\frac{1}{2}\left[\begin{array}{c}\sqrt{2}\\ \sqrt{2}\end{array}\right]$ 和 ${\mathbf{v}}_2=\frac{1}{2}\left[\begin{array}{c}-\sqrt{2}\\ \sqrt{2}\end{array}\right]$，特征向量矩阵 $V=\frac{1}{2}\left[\begin{array}{cc}\sqrt{2}& -\sqrt{2}\\ \sqrt{2}& \sqrt{2}\end{array}\right]$

\qquad 　　 特征值为 ${\lambda }_1=3,{\lambda }_2=1$，特征值对角阵 $D=\left[\begin{array}{cc}3& 0\\ 0& 1\end{array}\right]$
\qquad

图2 标准坐标轴方向不再是特征向量的方向：${\mathbf{e}}_1=[1,0{]}^T\ne k_1{\mathbf{v}}_1,{\mathbf{e}}_2=[0,1{]}^T\ne k_2{\mathbf{v}}_2$
“标准坐标轴方向”的单位向量 ${\mathbf{e}}_1$ 和 ${\mathbf{e}}_2$ 经过线性变换之后，在新的 $R^2$ 中为：$x_1^{{}^{\prime }}=2x_1+x_2,x_2^{{}^{\prime }}=x_1+2x_2$
也就是会改变大小和方向：${\mathbf{e}}_1^{{}^{\prime }}=A{\mathbf{e}}_1=[2,1{]}^T,{\mathbf{e}}_2^{{}^{\prime }}=A{\mathbf{e}}_2=[1,2{]}^T$。

\qquad

图3 由 $A{v}_i={\lambda }_i{v}_i$，特征向量 ${\mathbf{v}}_i$ 经过线性变换之后，在新的 $R^2$ 中方向不会改变，只是改变了长度：
$(1){\mathbf{v}}_1=\frac{1}{2}[\sqrt{2},\sqrt{2}{]}^T$ 方向上的尺度放大了 ${\lambda }_1=3$ 倍
$(2){\mathbf{v}}_2=\frac{1}{2}[-\sqrt{2},\sqrt{2}{]}^T$ 方向上的尺度放大了 ${\lambda }_2=1$ 倍（尺度没变）
　
也就是说，如果采用特征向量 ${\mathbf{v}}_1$ 和 ${\mathbf{v}}_2$ 作为基向量来构造 $R^2$，那么变换前后的 $R^2$ 仅仅是尺度发生了改变。

\qquad

3. 奇异值分解(Singular Value Decomposition,SVD)

\qquad 奇异值分解 $SVD$ 可以实现对一般矩阵 $A_{m\times n}$（非方阵）的对角化：

$A=U\Sigma V^T$　或者　$AV=U\Sigma$

\qquad\qquad 其中，$U_{m\times m}$ 和 $V_{n\times n}$ 都是正交矩阵
\qquad\qquad 　　　${\Sigma }_{m\times n}$ 是对角阵 $({\Sigma }_{ii}={\sigma }_i)$

\qquad

3.1 SVD的实质

\qquad 理解 $SVD$ 的本质，还得从线性变换的角度去看待，如图 $4$ 所示：

图4 在《向量空间基础》一文中已经说明：
$1)$ 对于一个秩为 $r$ 的矩阵 $A_{m\times n}$，其中必然包含着一个 $r\times r$ 的可逆方阵 ${\hat{A}}_{r\times r}$
$2)$ 线性变换 $A_{m\times n}:R^n\to R^m$，实际上是由 $A_{m\times n}:C(A^T)\to C(A)$ 完成（图中的 $A{\mathbf{x}}_r=\mathbf{b}$）
$3)$ 去掉空间$N(A)$和$N(A^T)$，线性变换 $A_{m\times n}:C(A^T)\to C(A)$ 实际上是指 $r$ 维子空间上的 ${\hat{A}}_{r\times r}:R^r\to R^r$
　
图片取自于《Introduction to Linear Algebra(Gilbert Strang)》Fig 4.3

\qquad 从线性变换的角度来看：矩阵 $A_{m\times n}$ 将 $R^n$ 中的向量变换为 $R^m$ 中的向量。
\qquad 然而，仅仅使用真实大小的可逆矩阵 $A_{r\times r}$ 来表示矩阵 $A_{m\times n}$ 的对角化，无法完整说明矩阵 $A_{m\times n}$ 作为 $R^n⟶R^m$ 线性变换的过程，只能说明实际的 $C(A^T)⟶C(A)$ 变换过程（图 $4$ 中的 $A{\mathbf{x}}_r=\mathbf{b}$），而 $C(A)$ 和 $C(A^T)$ 空间的实际维度都为 $r$ —— 都只有 $r$ 个线性无关的基向量。

\qquad
\qquad 因此，对于一个秩为 $r$ 的矩阵 $A_{m\times n}$，其 $SVD$ 对角化本质上是指 $r$ 维子空间上的可逆方阵 ${\hat{A}}_{r\times r}$ 所对应的线性变换 ${\hat{A}}_{r\times r}:R^r\to R^r$，也就是：

$\{\begin{array}{r}A{\mathbf{v}}_1={\sigma }_1{\mathbf{u}}_1\\ A{\mathbf{v}}_2={\sigma }_2{\mathbf{u}}_2\\ \\ A{\mathbf{v}}_r={\sigma }_r{\mathbf{u}}_r\end{array}⟹A\left[\begin{array}{ccc}& & \\ {\mathbf{v}}_1& \cdots & {\mathbf{v}}_r\\ & & \end{array}\right]=\left[\begin{array}{ccc}& & \\ {\mathbf{u}}_1& \cdots & {\mathbf{u}}_r\\ & & \end{array}\right]\left[\begin{array}{ccc}{\sigma }_1& & \\ & \ddots & \\ & & {\sigma }_r\end{array}\right]$

\qquad 奇异向量 $(singularvector){\mathbf{v}}_1,\cdots ,{\mathbf{v}}_r$ 都在 $A$ 的行空间 $C(A^T)$ 中，而 ${\mathbf{u}}_1,\cdots ,{\mathbf{u}}_r$ 都在 $A$ 的列空间 $C(A)$ 中。而且，奇异值 ${\sigma }_1,\cdots ,{\sigma }_r$ 都是正数（见 $3.3$ 节 结论 $1$）。

\qquad 因此，矩阵 $A_{m\times n}$ 的奇异值分解也可以写为：

\qquad\qquad $A=U\Sigma V^T=U_r{\Sigma }_r{V}_r^T={\mathbf{u}}_1{\sigma }_1{\mathbf{v}}_1^T+\cdots +{\mathbf{u}}_r{\sigma }_r{\mathbf{v}}_r^T$

\qquad
例3　　假设 $r=2,m=n=r$，奇异值分解的过程如图 $5$ 所示：
\qquad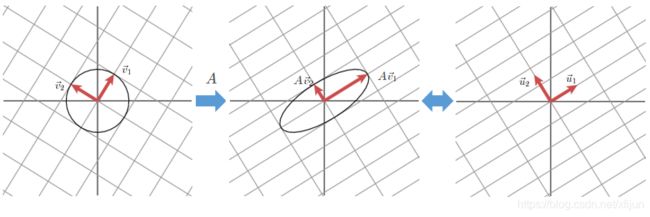

图5 与实对称矩阵的 $EVD$ 不同：
$(1)$ 奇异向量 ${\mathbf{v}}_i\in R^n$ 经过矩阵 $A_{m\times n}$ 变换为 $A{\mathbf{v}}_i\in R^m$ 之后 不一定满足方向不变
$(2)$ 将矩阵 $A_{m\times n}$ 变换后的向量 $A{\mathbf{v}}_1$ 和 $A{\mathbf{v}}_2$ 单位化，就是 $R^m$ 中的向量 ${\mathbf{u}}_1$ 和 ${\mathbf{u}}_2$
　　且满足 $A{\mathbf{v}}_1={\sigma }_1{\mathbf{u}}_1,A{\mathbf{v}}_2={\sigma }_2{\mathbf{u}}_2$（奇异值为长度）
$(3)$ 正交的奇异向量 ${\mathbf{v}}_1$ 和 ${\mathbf{v}}_2$，经过矩阵 $A_{m\times n}$ 变换为 $A{\mathbf{v}}_1$ 和 $A{\mathbf{v}}_2$ 后仍保持正交性，即：向量 ${\mathbf{u}}_1$ 和 ${\mathbf{u}}_2$ 也正交
　
【注】：本例中由于 $m=n=r=2$，因此两个零空间$N(A)=\{0\}$ 和 $N(A^T)=\{0\}$
　　
图1,2,3,5 均取自于：《We Recommend a Singular Value Decomposition》

\qquad
例4　　奇异值分解$A=U\Sigma V^T=U_r{\Sigma }_r{V}_r^T={\mathbf{u}}_1{\sigma }_1{\mathbf{v}}_1^T+\cdots +{\mathbf{u}}_r{\sigma }_r{\mathbf{v}}_r^T$ 过程描述

\qquad 图 $6(a)(b)$ 表示源空间，图 $6(c)$ 表示目标空间，矩阵 $A_{3\times 3}$ 的秩为 $r=2$，其 $SVD$ 过程为：

$(1)$ 图 $6(a)$ 中，$R^3$ 空间 ${\mathbf{v}}_3$ 轴上的所有向量经过 $A_{3\times 3}$ 变换后为 $0$，即零空间 $N(A)=\{k{\mathbf{v}}_3\}$

$(2)$ 在图 $6(a)$ 的 $R^3$ 空间中去掉零空间 $N(A)=\{k{\mathbf{v}}_3\}$，就变成了图 $6(b)$ 中的实际维度为 $2$ 的行空间 $C(A^T)$，即图 $6(b)$ 阴影区域所在平面

$(3)$ 从图 $6(b)$ 的行空间 $C(A^T)$ 中选择出正交的奇异向量 ${\mathbf{v}}_1,{\mathbf{v}}_2$，经过 $A$ 变换后就变成了图 $6(c)$ 中的向量 $A{\mathbf{v}}_1={\sigma }_1{\mathbf{u}}_1$ 和 $A{\mathbf{v}}_2={\sigma }_2{\mathbf{u}}_2$，向量 ${\mathbf{u}}_1,{\mathbf{u}}_2$ 仍保持正交性，以 ${\mathbf{u}}_1,{\mathbf{u}}_2$ 为基向量就构建出了实际维度为 $2$ 的列空间 $C(A)$，即图 $6(c)$ 阴影区域所在平面

$(4)$ 奇异值分解 $A=U\Sigma V^T=U_r{\Sigma }_r{V}_r^T$ 实际上是指 ${\hat{A}}_{2\times 2}:C(A^T)\to C(A)$
\qquad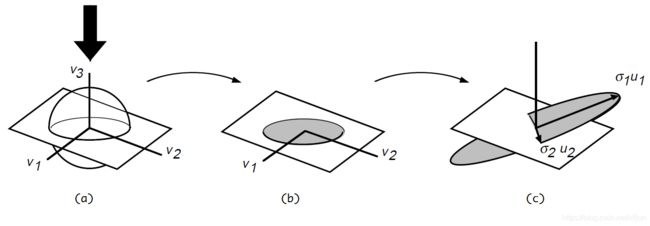

图6 取自于《A Singularly Valuable Decomposition: The SVD of a Matrix》Fig.2

\qquad

3.2 SVD的奇异向量(Singular vector)

\qquad 由上节分析可知，只考虑用 ${\mathbf{v}}_1,\cdots ,{\mathbf{v}}_r$ 作为基向量构建行空间 $C(A^T)$ 、以及用 ${\mathbf{u}}_1,\cdots ,{\mathbf{u}}_r$ 作为基向量构建列空间 $C(A)$ 来完成 $SVD$ 显然不足以描述线性变换 $A_{m\times n}:R^n⟶R^m$ 的完整过程，还必须完成以下内容：

• 使用正交矩阵 $V_{n\times n}$ 中的所有列向量 $\{{\mathbf{v}}_i{\}}_{i=1}^n$ 构建 $R^n$ 空间

$(1)$ 由于 $r$ 个线性无关的 ${\mathbf{v}}_1,\cdots ,{\mathbf{v}}_r$ 都在 $A$ 的行空间 $C(A^T)$ 中，实际上只是构成了 $R^n$ 中的子空间 $R^r\subseteq R^n$，并不足以构成整个 $R^n$

$(2)$ 由于行空间 $C(A^T)$ 在 $R^n$ 中的正交补空间为零空间 $N(A)$，为了构建整个 $R^n$，还必须补充构成 $N(A)$ 的 $n-r$ 个 $\{{\mathbf{v}}_i{\}}_{i=r+1}^n$ 基向量，也就是要使用到 $V_{n\times n}$ 的全部列向量 $\{{\mathbf{v}}_i{\}}_{i=1}^n$

零空间 $N(A)$ 中的 $n-r$ 个 $\{{\mathbf{v}}_i{\}}_{i=r+1}^n$ 基向量，均与行空间 $C(A^T)$ 中的 ${\mathbf{v}}_1,\cdots ,{\mathbf{v}}_r$ 正交
　
由于 $A{\mathbf{v}}_i=0\in R^m,\forall v_i\in N(A)\subset R^n$，矩阵 $A$ 将 $N(A)$ 中的向量变换为了 $R^m$ 的原点
也就是说，$N(A)$ 中的向量没能真正体现出“矩阵 $A$ 作为线性变换”应有的作用，可以认为是“冗余的”

• 使用正交矩阵 $U_{m\times m}$ 中的所有列向量 $\{{\mathbf{u}}_i{\}}_{i=1}^m$ 构建 $R^m$ 空间

$(1)$ 由于 $r$ 个线性无关的 ${\mathbf{u}}_1,\cdots ,{\mathbf{u}}_r$ 都在 $A$ 的列空间 $C(A)$ 中，实际上只是构成了 $R^m$ 中的子空间 $R^r\subseteq R^m$，并不足以构成整个 $R^m$

$(2)$ 由于列空间 $C(A)$ 在 $R^m$ 中的正交补空间为左零空间 $N(A^T)$，为了构建整个 $R^m$，还必须补充构成 $N(A^T)$ 的 $m-r$ 个 $\{{\mathbf{u}}_i{\}}_{i=r+1}^m$ 基向量，也就是要使用到 $U_{m\times m}$ 的全部列向量 $\{{\mathbf{u}}_i{\}}_{i=1}^m$

左零空间 $N(A^T)$ 中的 $m-r$ 个 $\{{\mathbf{u}}_i{\}}_{i=r+1}^m$ 基向量，均与行空间 $C(A)$ 中的 ${\mathbf{u}}_1,\cdots ,{\mathbf{u}}_r$ 正交
　
由于 $A^T{\mathbf{u}}_i=0\in R^n,\forall u_i\in N(A^T)\subset R^m$，矩阵 $A^T$ 将 $R^m$ 中的一些向量 ${\mathbf{u}}_i\in N(A^T)$ 变换为了 $R^n$ 的原点
因此，$N(A^T)\subset R^m$ 中的这些向量对于变换 $A^T$ 而言也是“冗余的”

\qquad
\qquad 使用所有 $\{{\mathbf{u}}_i{\}}_{i=1}^m$ 和$\{{\mathbf{v}}_i{\}}_{i=1}^n$ 构建了完整的 $R^m$ 和 $R^n$ 之后， 矩阵 $A_{m\times n}$ 作为 $R^n⟶R^m$ 的线性变换过程才得以完整体现。此时，完整的奇异值分解就表示为 $AV=U\Sigma$，也就是：
\qquad
$A\underset{V_{n\times n}}{\left[\begin{array}{c}\\ {\mathbf{v}}_1\cdots {\mathbf{v}}_r\cdots {\mathbf{v}}_n\\ \end{array}\right]}=\underset{U_{m\times m}}{\left[\begin{array}{c}\\ {\mathbf{u}}_1\cdots {\mathbf{u}}_r\cdots {\mathbf{u}}_m\\ \end{array}\right]}\underset{{\Sigma }_{m\times n}}{\left[\begin{array}{cccc}{\sigma }_1& & & \\ & \ddots & & \\ & & {\sigma }_r& \\ & & & \end{array}\right]}$

\qquad 或者 $A=U\Sigma V^T=U_r{\Sigma }_r{V}_r^T$ 的形式：

$\begin{array}{rl}A& =\left[\begin{array}{c}{\mathbf{u}}_1\cdots {\mathbf{u}}_r|{\mathbf{u}}_{r+1}\cdots {\mathbf{u}}_m\end{array}\right]\left[\begin{array}{cccccc}{\sigma }_1& & & 0& \cdots & 0\\ & \ddots & & ⋮& 0& ⋮\\ & & {\sigma }_r& ⋮& 0& ⋮\\ 0& \cdots & 0& 0& \cdots & 0\\ ⋮& 0& ⋮& ⋮& \ddots & ⋮\\ 0& \cdots & 0& 0& \cdots & 0\end{array}\right]\left[\begin{array}{c}{\mathbf{v}}_1^T\\ ⋮\\ {\mathbf{v}}_r^T\\ ——\\ {\mathbf{v}}_{r+1}^T\\ ⋮\\ {\mathbf{v}}_n^T\end{array}\right]\\ & =\underset{U_r{\Sigma }_r{V}_r^T}{\left[\begin{array}{c}{\mathbf{u}}_1\cdots {\mathbf{u}}_r\end{array}\right]\left[\begin{array}{ccc}{\sigma }_1& & \\ & \ddots & \\ & & {\sigma }_r\end{array}\right]\left[\begin{array}{c}{\mathbf{v}}_1^T\\ ⋮\\ {\mathbf{v}}_r^T\end{array}\right]}+\left[\begin{array}{c}{\mathbf{u}}_{r+1}\cdots {\mathbf{u}}_m\end{array}\right]\left[\begin{array}{ccc}& & \\ & 0& \\ & & \end{array}\right]\left[\begin{array}{c}{\mathbf{v}}_{r+1}^T\\ ⋮\\ {\mathbf{v}}_n^T\end{array}\right]\end{array}$

\qquad

3.3 SVD奇异向量与EVD的关系

\qquad
结论1 右奇异向量矩阵 $V_{n\times n}=[{\mathbf{v}}_1,\cdots ,{\mathbf{v}}_n],{\mathbf{v}}_i\in R^n$ 是实对称矩阵 $A^{T}A$ 的特征分解 $EVD$ 的特征向量集，且实对称矩阵 $A^{T}A$ 的特征值都是非负的，矩阵 $A_{m\times n}$ 进行 $SVD$ 后的奇异值都是非负的。

$A^{T}A=VD{V}^T$
\qquad\qquad 其中，正交矩阵 $V_{n\times n}=[{\mathbf{v}}_1,\cdots ,{\mathbf{v}}_n],{\mathbf{v}}_i\in R^n$ 就是 $SVD$ 的右奇异向量矩阵
\qquad\qquad 　　　对角阵 $D_{n\times n}$ 的对角线元素 ${\lambda }_i$ 为 $A^{T}A$ 的特征值，假设特征值在对角线上以降序排列

\qquad 由于：
$A^{T}AV=VD⟹A^{T}A{\mathbf{v}}_i={\lambda }_i{\mathbf{v}}_i$

\qquad 可得：
$\begin{array}{rl}(A{\mathbf{v}}_i{)}^T(A{\mathbf{v}}_j)& ={\mathbf{v}}_i^T{A}^{T}A{\mathbf{v}}_j\\ & ={\mathbf{v}}_i^T({\lambda }_j{\mathbf{v}}_j)\\ & ={\lambda }_j{\mathbf{v}}_i^T{\mathbf{v}}_j\\ & =0\end{array}$

\qquad 这就说明，正交矩阵 $V_{n\times n}$ 中正交的列向量 $\{{\mathbf{v}}_1,\cdots ,{\mathbf{v}}_n\},{\mathbf{v}}_i\in R^n$，经过矩阵 $A_{m\times n}$ 变换为 $R^m$ 中的 $\{A{\mathbf{v}}_1,\cdots ,A{\mathbf{v}}_n\},A{\mathbf{v}}_i\in R^m$ 后，仍然是正交的。

\qquad
\qquad 因此：

$(A{\mathbf{v}}_i{)}^T(A{\mathbf{v}}_j)⟹\{\begin{array}{rlr}(A{\mathbf{v}}_i{)}^T(A{\mathbf{v}}_j)& ={\lambda }_j{\mathbf{v}}_i^T{\mathbf{v}}_j=0& ,i\ne j\\ & & \\ (A{\mathbf{v}}_i{)}^T(A{\mathbf{v}}_i)& =\Vert A{\mathbf{v}}_i{\Vert }^2={\lambda }_i\ge 0& ,i=j\end{array}$

\qquad 这就说明，实对称矩阵 $A^{T}A$ 的特征值 ${\lambda }_i$ 都是非负的。

\qquad 又因为，在 $SVD$ 中满足 $A{\mathbf{v}}_i={\sigma }_i{\mathbf{u}}_i,i\in \{1,\cdots ,r\}$，因此：

${\mathbf{u}}_i=\frac{A{\mathbf{v}}_i}{\left|A{\mathbf{v}}_i\right|}=\frac{1}{\sqrt{{\lambda }_i}}A{\mathbf{v}}_i=\frac{1}{{\sigma }_i}A{\mathbf{v}}_i,i\in \{1,\cdots ,r\}$

\qquad 这就说明，矩阵 $A_{m\times n}$ 进行 $SVD$ 后的奇异值 ${\sigma }_i=\sqrt{{\lambda }_i}\ge 0$ ，都是非负的。

\qquad
结论2 左奇异向量矩阵 $U_{m\times m}=[{\mathbf{u}}_1,\cdots ,{\mathbf{u}}_m],{\mathbf{u}}_i\in R^m$ 是实现实对称矩阵 $A{A}^T$ 的特征分解 $EVD$ 的特征向量集，而且具有与实对称矩阵 $A^{T}A$ 相同的非零特征值。

\qquad 由于满足$A{\mathbf{v}}_i={\sigma }_i{\mathbf{u}}_i,i\in \{1,\cdots ,r\}$

\qquad 又因为：
${\mathbf{u}}_i=\frac{1}{\sqrt{{\lambda }_i}}A{\mathbf{v}}_i=\frac{1}{{\sigma }_i}A{\mathbf{v}}_i,i\in \{1,\cdots ,r\}$

\qquad 因此：

$\begin{array}{rl}A{A}^T{\mathbf{u}}_i& =A{A}^T\left(\frac{1}{{\sigma }_i}A{\mathbf{v}}_i\right)\\ & =\frac{1}{{\sigma }_i}A(A^{T}A{\mathbf{v}}_i)\\ & =\frac{1}{{\sigma }_i}A({\lambda }_i{\mathbf{v}}_i)\\ & =\frac{1}{{\sigma }_i}{\lambda }_i(A{\mathbf{v}}_i)\\ & =\frac{1}{{\sigma }_i}{\lambda }_i({\sigma }_i{\mathbf{u}}_i)\\ & ={\lambda }_i{\mathbf{u}}_i\end{array}$

\qquad 也就是 $A{A}^{T}U=UD$ 或者 $A{A}^T=UD{U}^T$

\qquad 这就说明，实对称矩阵 $A{A}^T$ 具有与实对称矩阵 $A^{T}A$ 相同的非负特征值 ${\lambda }_i\ge 0,i\in \{1,\cdots ,r\}$。
\qquad
\qquad
【注】：关于向量空间的基本概念，请参考《向量空间基础知识》