量子力学 or 线性代数（Stern-Gerlach实验）？

一. 实验背景

1920-1922年间,德国科学家O. Stern和 W. Gerlach用高温产生的银原子束在一不均匀的磁场中发生偏转得到2条裂痕的结果,第一次通过简洁的宏观实验验证了A. Sommerfeld等人提出的“微观原子世界的角动量具有空间量子化特征”假说,这一结论也被随后诞生的量子力学所证明. Stern-Gerlach实验提供了测量原子磁矩的一种方法,在此基础上进一步发展的原子束和分子束技术,使Stern获得了1943年的诺贝尔物理学奖。该实验也是1925年G. E. Unlenbeck和S. A. Goudsmit提出电子自旋假设,并确定自旋磁矩大小的重要实验依据之一,不同纠缠量子态的粒子在磁场中分离，是当今量子信息研究热点。正是因为它如此重要，为了给后面量子力学的学习铺路，今天大家一起来学习一下这个 相对来说比较复杂的实验。（大家可以自行百度，大物里面应该都有这个实验 ，但是IT专业的学生可能会有点费劲，比如我）。

本次可能需要大家拥有比较扎实的高中物理电磁学的基础知识，和数学能力，和前 2 次 的博客有所不同，毕竟科学的殿堂是庄严肃穆的，嬉皮笑脸的肯定是不行的！

二 . 实验准备

小伙伴们，先和我一起把记忆拉回到我们共同 怀恋的 ，青涩的 高中时代，高二开始，几乎所有的理科生一起抱着必死的决心 踏上了物理电磁学的不归路（手动滑稽）。。。。
多说无益，先上图：

根据我残破不堪的高中知识，我们知道；这个磁感线是不均匀的穿过这个线圈，且线圈中存在一个逆时针方向的电流（自上向下看），这种情形下，线圈将受到一个向上的安培力 F （姑且先这样认为），其大小和电流强度 $I$ 、线圈围成的面积 $S$ 、磁感应强度的变化率$\frac{\Delta B}{\Delta t}$成正比,即：
$$F=IS\cdot \frac{\Delta B}{\Delta t}$$
注意，这里我们介绍一个新的有关上述表达式的物理量：$\mu =I\cdot S$ ，叫做 “磁矩”。

所以上述安培力$F$可以表示为：$F=\mu \cdot \frac{\Delta B}{\Delta t}$，由于后面实验多次用到 磁矩 的概念，我们在这里简介一下：

磁矩：描述载流线圈或微观粒子磁性的物理量，是一个有方向的矢量，它的方向垂直于线圈所在平面，在均匀外磁场中，平面载流线圈所受合力为零而所受力矩不为零，该力矩使线圈的磁矩m转向与外磁场B的方向相同的方向；在均匀径向分布外磁场中，平面载流线圈受力矩偏转。

在高中我们就知道磁感线与线圈的方向即二者之间的夹角也会对 $F$产生比较大的影响，这个点我们在下面实际试验的时候再说。

上述公式，$F$ 只是一个计算式，为了更适用现实情况，我们将这个式子改写为一个更普适的矢量式：
$$F=▽(\mu \cdot B)$$
这里出现了哈密顿算子，后续数学公式推导的实现需要，在这里我们只要简单的学一下就好：

记号读作“那勃勒”，在运算中既有微分又有矢量的双重运算性质，其优点在于可以把对矢量函数的微分运算转变为矢量代数的运算，从而可以简化运算过程，并且推导简明扼要，易于掌握。

到这里我们做这个试验必备的知识点已经解决一半了 ，但是剩下的一半才是最重要的。同样是回忆高中“美好”的时光，这次将我们记忆的曲线变成以化学为横坐标的时光轴。在物质的《结构与性质》中，我们都知道一个原子核外电子会绕着原子核做圆周运动，并且我们将核外轨道分为 $s,p$ 等能级，基态和激发态 的电子填充规律（遵循泡利原理和洪特规则）等等，除此之外，我们还知道的是每个电子的都存在自旋，且在一个能级的同一个轨道中，2个电子的自旋方向是相反的，下图的2个原子例子我相信你能很快就回忆起来：

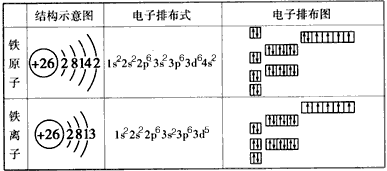
现在我们结合上面刚刚讲解的磁矩的知识，电子在绕和做圆周运动的时候 会产生微弱的感应带电流，同样 ，自旋的时候也会产生。特别注意的是：电子的自旋不是我们所理解的电子的自转，不能和地球公转与自转相类比，电子自旋是量子效应，不能作经典的理解，如果把电子自旋看成绕轴的旋转，则得出与相对论矛盾的结果）。这个时候，由于自旋就会产生磁矩，成为“自旋磁矩”, 其具有固定的大小，后面我们都用$\mu$ 来表示这个自旋磁矩。

三 . 实验过程

实验用具是:一个加热炉、两个挖了小圆孔的挡板、一对磁极和一个接收屏.
就像这样，看上去比较简单：

我们这里在加热炉中对 银子（没错，就是金属银）加强热，使得银原子向各个方向发射大量的银原子，两个挖了小圆孔的挡板是为了筛选出 运动轨迹为一条直线 且方向磁场方向飞去的符合标准的银原子。这些银原子通过两块磁铁间分布于$Z$轴方向的不均匀磁场后，会到达接收屏形成光斑。。。

四 . 实验结果

（1）猜测结果：

刚刚我们才讲过，银原子中电子的磁矩是使得银原子在图示中 $z$ 轴方向上 磁场中发生一切偏转的动力，再根据我们前面 实验准备 中讲的 泡利原理 和 洪特规则 ，银原子的 $47$ 核外电子中，前$46$个每2个的电子（即在同一轨道能级上的，假设这里的所有银原子都处于基态。）的自旋方向相反，所以真正起作用的就是最后一个电子的自旋磁矩。

换句话说，银原子的整体磁矩大小就等于1个电子的自旋磁矩大小 $\mu$ 。
下面我们来推导一下：磁矩的方向。

之前我们将 $F$使用哈密顿算子表示为：$F=\mu \cdot \frac{\Delta B}{\Delta t}$
展开成分量形式为：

显然，根据装置我们可以一眼看出这个偏转的力来自$Z$轴方向，我们只需要取$Z$轴方向即可。。

同理，只取$Z$轴方向上的，最后我们得到的最终结果为：$F_z={\mu }_z\frac{\partial B_z}{{\partial }_z}$

因为每一个银原子的磁矩大小是确定的，就是一个电子的自旋磁矩大小，但是它的方向是随机的，每一个银原子的可能都是不一样的，这里我们可以先假设某颗银原子进入磁场前，磁矩方向与 $+Z$ 方向成 $\theta$ 角度,那么磁矩的 $z$ 分量就是${\mu }_z=\mu cos\theta$，于是银原子飞入磁场后，受力大小就是： $$F_z={\mu }_z\frac{\partial B_z}{{\partial }_z}cos\theta$$
按照高中我们已经学习的经典物理的理解，由于银原子的磁矩方向随机，所以不同的银原子的磁矩方向 $\theta$ ，可以在 0 到 $\pi$之间任意取值，并且机会均等,，所以，银原子所受的力 $F_z$ 和加速度 $a$ 的取值区间为：

$$-\mu \frac{\partial B}{\partial z}\le F_z\le \mu \frac{\partial B}{\partial z}$$
$$-\frac{\mu }{m}\frac{\partial B}{\partial z}\le F_z\le \frac{\mu }{m}\frac{\partial B}{\partial z}$$
如果这样解释的话，最后，当足够多个银原子打到接收屏上后，这些轨迹会在屏幕上形成一条 $Z$方向上的连续线段.
当然这个我们猜测的，实践是检验真理的唯一标准。

（2）真实结果：

相信你已经知道了，如果那么简单，那我们学这个干嘛，和量子力学有个P关系。。
真实结果为:

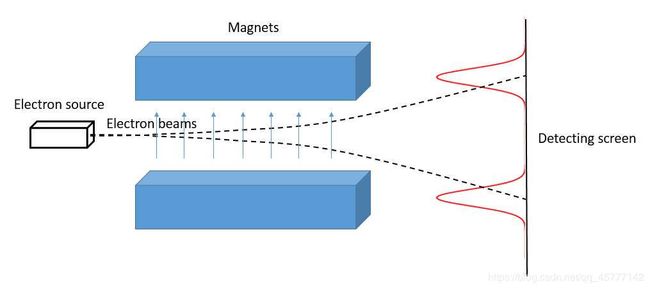
和我们猜测的结果不同的地方在于：银原子一进入磁场，就自动劈裂了泾渭分明的两条轨迹，最后在屏幕上打出两个分离的斑点，介咋嘛和偶们想的不一样啊！！！

五. 实验结果分析解释

虽然经典想法中的随机性会让我们认为打出来的点会均匀的分布以形成一条连续的直线。但实验结果却告诉我们，这个猜测并不对，实验结果背后隐藏的真正的随机性，其实是来自量子层面的，这个时候，我们前面学的叠加态知识在这里就能大展身手了！！

对于任意一颗银原子，只要我们不去测量它在某个方向上(比如 $Z$轴 方向上 )的磁矩，它就处于量子叠加态，而没有确定的方向。而只有当我们去测量它的磁矩时，它才会随机坍缩到这个测量行为所对应的本征态上，被我们测量到，换句话说，测量结果只能是被测量的物理量对应的本征态之一。而我们这个实验就相对于是一种测量磁矩的手段。

所以，如果我们去测量它在$Z$方向的磁矩,那么测量结果就只能是“ Z方向磁矩”这个物理量的两个本征态，这正好就是“磁矩处于 $-Z$方向”和“磁矩处于 $+Z$ 方向”两个结果，于是我们就看到，大量银原子通过磁场后，会形成两条泾渭分明的轨迹。

这个我们还要注意一个问题：我们前面学习过 叠加态测量后会坍缩到本征态，而本征态在态空间中是相互正交的，但是在这个实验中我们发现，在宏观世界中，$-Z$轴与$+Z$轴之间的夹角是 $\pi$ ,并不是正交的。

如果将两个本征态在态空间中的“夹角”记为 $\phi$ 、在真实空间中的夹角记为 $\theta$，那么从上面的分析可以看出，它们之间似乎有着简单的倍数关系： $\theta =2\phi$,是巧合 ，还是必然，后面的陆续学习中我们会逐渐揭晓谜底。。。。。

六 . 级联SG实验

为了更加深刻的解释实验的本质，我们在原有的简单基础上又再次进行三次加强版实验（级联实验）。

（1）级联 S
前面简单的SG实验中，银原子分成了上下两束，说明测量银原子 $Z$ 方向自旋时，原本处于叠加态的银原子状态，随机落到了两个本征态上,我们在这里将这两个本征态分别记为：$|Z_{+}>,|Z_{-}>$。

在这个实验中，我们需要改动的地方是：我们将原来实验装置中的接收屏撤掉，让其中处于 $|Z_{+}>$ 态的银原子(也就是向上走的那一束银原子 )继续往前走。

经典直觉告诉我们：这束银原子具有确定的磁矩方向，即 +Z方向，所以它们通过第二个S-G装置时，依然会向上偏转，而实验的结果也告诉我们的猜测是正确的，就像我们之前用棒棒糖举例的方法一样，当我们测量了它的颜色之后，只要我们不去尝它，无论看多少次，它的颜色都不会再发生改变了。

根据我们 残破不堪 的线性基础知识可以知道：任意向量都可以表示成某个线性算子的一组完备特征向量(也就是一组完备基底)的线性组合。

所以，根据我们前面学过的知识：银原子的任意量子态 $|\phi >$ ，也都可以表示成两个本征态的叠加：
$|\phi >=k_{z+}|Z_{+}>+k_{z-}|Z_{-}>$ 且 ${\left|k_{z+}\right|}^2+{\left|k_{z-}\right|}^2=1$,其中，两个本征态前面的系数 ${\left|k_{z+}\right|}^2,{\left|k_{z-}\right|}^2$就分别对应这个银原子向上偏转和向下偏转是的相应磁矩的概率。

这对本征态本身也成立，比如对于处于 $|Z_{+}>$ 的银原子，它的状态就是：$|Z_{+}1>=1|Z_{+}>+0|Z_{-}>$。
本身已经坍缩到本征态的银原子，我们在用同样的方法去测量它，它还是以1的概率到Z轴的正方向上。

（1）级联 SS

在这次实验中，我们将改变磁场的方向，再来看一看到底发生什么:
首先，我们仍然从简单版的S-G实验装置中筛选出 $|Z_{+}>$ 的银原子，并且撤去接收屏，让这束银原子通过一个通过磁场沿 $X$方向的S-G实验装置, 图示如下：

如果我们还是以经典力学的思维思考的话，会认为 原本筛选出来的磁矩是z轴正方向，所以进入Y轴方向的磁场之后，由于z轴与x轴是相互垂直的，此时，$cos\theta$ = 0，于是，银原子受到的磁场力大小为 $F=0$，但是，吃一堑长一智，这里我并不这么认为，我认为，即使是已经筛序出来的银原子还是会随机的向 $+x$ 和 $-x$方向飞去，并形成两个明显的点。

事实结果证明, “反其道行之” 往往才是正确的，的确，还会分成2个点，并不会不受磁场力的作用，用量子叠加态解释就是：

对于$|Z_{+}>$ 态的银原子，如果去测量它的 $x$方向磁矩，那么银原子的状态会随机坍缩到 $x_{+}>$ 和 $|x_{-}>$ 中的任意一个，因为在这里$x$方向的两个本征态和$z$轴方向的两个本征态是不一样的。

再根据我们前面介绍本征态的正交性和叠加态的知识，我们可以推知： Z 方向自旋磁矩处于确定的本征态时，X 方向自旋磁矩就处于不确定的叠加态 (这里又一次看到了不确定性原理的影子 )

注意这里我们同时出现了四个本征态！前面我们曾经用一个图形象的表示了二维平面内 四个本征态的相互关系：

所以，我们可以根据这个大胆的推测，此时的四个本征态关系为：
$$|Z_{+}>=\frac{1}{\sqrt{2}}|x_{+}>+\frac{1}{\sqrt{2}}|x_{-}>,|Z_{-}>=-\frac{1}{\sqrt{2}}|x_{+}>+\frac{1}{\sqrt{2}}|x_{-}>$$
这个还有待验证，日后再叙。

（1）级联 SSS
这个实验的目的就是对我们前面得到结论有一个“验证”的作用。

步骤:
先让银原子通过一个 $S{G}_z$装置，从中筛选出 $|Z_{+}>$ 那束银原子，让它们通过一个 $S{G}_x$ 装置，然后从中又筛选出 $|x_{+}>$的银原子，让它们再次通过一个 $S{G}_z$装置,看一看结果是怎么样的。
很显然，我们这样做的目的就是：看看这些银原子是否还“记得”自己在上次通过$S{G}_x$前，“曾经”是 $|Z_{+}>$
同样，我相信大家这次都会大胆猜测：还是会分开，形成明显的两个点在Z轴竖直线上。

结果也必然和我们猜测的一样。

关于SG实验的大概内容我们到这里也就结束啦！都看到这了，就用您那发财的小手指点点赞吧！！