量子力学 or 线性代数(四)?
真正的入门
- 一. 特征值与特征向量
- 二. 本征矢,本征值和量子测量
- 三. 两个例子
- (1)SG实验.
- (2)氢原子能级.
一. 特征值与特征向量
看到这个标题就知道这次我们先从线性代数入手,从前面的几次学习中,我们已经大概知道量子力学的一些基本知识和线性代数的联系。但是在上次课中的S-G实验中 似乎并没有线性代数的参与,在这次课中的结尾,会为大家揭晓这一惊天秘密。。(手动微笑~)
先让我们回顾一下大一学习的线代知识,其中最重要的,考试最喜欢考的一节内容就是:特征值与特征向量。
那这么重要的知识在量子力学中有没有特定的物理意义,或者是和量子力学有关的特定概念和数学意义呢?
好,以此为起点,正式进入今天的学习。不知道大家知不知道旋转矩阵这个概念,我们先来看一个小题目:
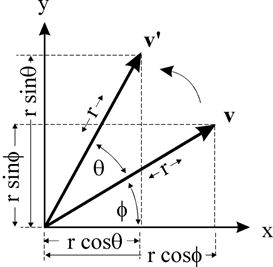
如图所示,假设二维平面中有一个向量 V V V,现在存在一个旋转矩阵 R θ R_{\theta } Rθ 使得, V ′ = R θ V V{}' = R_{\theta } V V′=RθV,那么,易知,这个旋转矩阵为: R θ = [ c o s θ s i n θ − s i n θ c o s θ ] R_{\theta }= \left[ \begin{matrix} cos\theta & sin\theta \\ -sin\theta & cos\theta \end{matrix} \right] Rθ=[cosθ−sinθsinθcosθ]
显然,它作用在向量上时,会把向量旋转 θ \theta θ 角而不改变其大小.当我们想直接改变矩阵的大小而不改变其方向时,我们乘的是: [ λ 0 0 λ ] \left[ \begin{matrix} \lambda & 0 \\ 0 & \lambda \end{matrix} \right] [λ00λ]
除此之外,对于一些矩阵而言,不管它作用在其他向量上时会造成怎样的改变,我们总是能找到一些特殊的向量,使得这个矩阵只能改变其“大小”,而不改变其方向,这时候我们主角之一的 特征向量 就隆重登场了。而它的“大小”改变的比例,就是相应的 特征值。
二. 本征矢,本征值和量子测量
开门见山,其实本征矢(Eigen Vector) 就是前面我们所说的 特征向量,细心的同学会发现 这个2个名词的英文单词都是一样的。而以此类推,不难猜,本征值就是 特征值。
在前面我们已经学过,一个物理量会对应一组本征态,就像一个矩阵可能会对应一组特征向量。
既然一组本征态的数学本质就是一组特征向量,那么它背后对应的那个物理量,在量子力学中是不是也会对应一个矩阵呢?

在这里,我们将介绍量子力学中(当然不仅仅用在量子力学上)的另一个重要的概念:算符,若现在有一个物理量为 P P P,那么它的算符就是 P P P 上加个小尖帽 ,记作: p ^ \widehat{p} p 。那它有啥子作用勒???
使问题从一种状态变化为另一种状态的手段称为操作符或算符。算符在单独存在时是没有什么意义。
量子物理学中,算符是一个函数,作用于物理系统的物理态 (physical state),使这个物理态变换为另外一个物理态,算符概念也是理论表述不可缺少的一部分。
现在,我们可以这样说:当我们对一个处于叠加态 ψ \psi ψ 的物理对象(假设是一个微观粒子 )测量物理量 P P P的时候,体现在数学上,就是 P P P 的算符 p ^ \widehat{p} p 作用在 ψ \psi ψ 上。
注意这里的“作用”两个字,这个词的含义用线代知识来解释就是:将 ∣ ψ > |\psi> ∣ψ> 类比成一个列向量 α \alpha α ,将 P ^ \widehat{P} P 类比成一个矩阵 A A A ,那么上面引号里那句话,其实就是矩阵 A A A 左乘向量 α \alpha α,或者说 A A A 作用在 α \alpha α 上。
当然了,如果这么解释的话,大家可能都会发现:这样我们原来的向量 α \alpha α就会发生一定程度上的改变啊,我去! 这个怎么那么熟悉啊?? 是不是在哪里见过,等一下~~噢呕 ~ 这个怎么和我们前面的棒棒糖(不记得的大哥们赶紧回去翻前面的博客卡看~)这么相似啊 !!
难道我们使用这个算符 p ^ \widehat{p} p 作用在 ψ \psi ψ上的原理和前面的一样 或者说有什么相似之处吗?
且看我柯蓝附体慢慢道来:

在前面的学习中,我们已经知道了,测量一个物理对象的某个物理量 P P P 时,当其处于叠加态的时候,测量过程会使它 坍缩 到其中一个本征态上,它的量子态也就因此改变,但是,在特殊情况下,测量一个物理对象的某个物理量 P P P时,不会改变它的量子态,这种情况,就是这个对象的量子态正好是 P P P 的本征态,也就是算符 p ^ \widehat{p} p 的本征矢。
在线代中:如果向量 α \alpha α假设是矩阵 A A A 的特征向量,那么 A A A 左乘 α \alpha α,会得到
A α = λ α A\alpha =\lambda \alpha Aα=λα
和前面介绍的一样,这样的处理只会改变“大小”,不会改变“方向”,那么同样的,我们平移到量子力学中来说:
当我们使用一个像算符一样的方法去作用该物体的其中一个已经处于本征态的物理量的时候,是否也会像上面的例子一样,只改变所谓的“大小”(乘以一个特征值),而不改变“方向”呢?
其实,在量子力学中,态矢量中 并没有“大小”之说,只有所谓的“角度”(后面我们会学到这个!),这也就能解释:为什么算符作用在它的本征态上时这个本征态不会被改变了。但是,我们前面说了那么多,难道真正的量子力学中只有一种本征矢和线代中的特征向量对应吗?本征值真的就不存在吗??
其实不是。。。往往最重要的东西,在现实生活中是最难发现的 一般也是最后才能发现,哼 ! 正所谓
蓦 然 回 首 , 那 人 却 在 灯 火 阑 珊 处 蓦然回首,那人却在灯火阑珊处 蓦然回首,那人却在灯火阑珊处
其实这个我们找不到的本征值(特征值)就是联系量子和经典物理的桥梁,换句话说:物理量算符作用到本征态上得到的特征值,就是经典世界中测量到的物理量的值 !!!
For example:
比如有一个 X X X 方向上确定动量的粒子(这意味着它的量子态正好是动量算符 P x ^ \widehat{P_{x}} Px 的某一个本征态 ∣ P x > |P_{x}> ∣Px>),去测量它的动量时,测得的动量值 P x P_{x} Px,就是相应的特征值,数学表达式为:
P x ^ ∣ P x > = P x ∣ P x > \widehat{P_{x}}|P_{x}> =P_{x}|P_{x}> Px ∣Px>=Px∣Px>
将上面的所有部分过程简化为一句话就是:当粒子的量子态处于动量算符的某个本征态 ∣ P x > |P_{x}> ∣Px>,我们通过某种手段去测量它的动量后, ∣ P x > |P_{x}> ∣Px>仍然不会改变,但特征值信息会被“释放”出来,表现成测量仪器上的读数 P x P_{x} Px。
OMG!真是盖了帽了,我的老北鼻!!(手动滑稽~~)
然而,上述的情况所需要的前提是:该物理量已经处于本征态,若是其处于非本征态呢?又当如何?
这可又难住老铁们了!

好吧,先让我们把目光的焦点回到线代上,在线代的线性相关性上,我们知道:假设矩阵 A A A有不同的特征值 λ 1 , λ 2 . . . λ n \lambda_{1}, \lambda_{2} ...\lambda _{n} λ1,λ2...λn,以及相应的特征向量 α 1 , α 2 , . . . α n \alpha_{1}, \alpha_{2},...\alpha_{n} α1,α2,...αn。显然,这些特征向量构成一组线性无关的基底,此时,我们可以假设某一个向量 V V V可以由 α 1 , α 2 , . . . α n \alpha_{1}, \alpha_{2},...\alpha_{n} α1,α2,...αn线性表示:
V = c 1 α 1 + c 2 α 2 + . . . + c n α n V=c_{1}\alpha _{1} +c_{2}\alpha _{2} +...+c_{n}\alpha _{n} V=c1α1+c2α2+...+cnαn
这个时候,我们用矩阵 A A A作用于 V V V上得到的新向量是什么呢?
A V = λ 1 c 1 α 1 + λ 2 c 2 α 2 + . . . + λ n c n α n AV=\lambda _{1}c_{1}\alpha _{1} +\lambda _{2}c_{2}\alpha _{2} +...+\lambda _{n}c_{n}\alpha _{n} AV=λ1c1α1+λ2c2α2+...+λncnαn
我相信,您只要学过线性代数,就一定知道,上面的这个两个向量只是系数不一样,并没有产生新的特征向量。
那么,再回到我们刚才的那个问题上:对不处于动量本征态的粒子测量动量时,会不会得到另一个非本征态呢?
我相信只要前面的博客您认真地看了的话,一定知道:不会。
我们前面说过,当处在叠加态的一个物理量被测量时,它会根据概率随机坍缩到其中的一个本征态上,并不会坍缩到我们所希望的另一个本征态。当然了,与此同时,随机坍缩发生后,该物理量 对应的一个本征值会作为测量结果的数值信息被“释放”出来。
三. 两个例子
介绍了上面那么多的内容,接下来我们以2个例子来帮助大家更好的理解和学习。
(1)SG实验.
上个微博中我们向大家详细的介绍了一下S-g实验,我们现在再来一起回顾一下:
银原子通过SG实验装置后,泾渭分明地分裂成了两束,也就是测量它的 z z z方向自旋时,银原子的量子态坍缩到 ∣ Z + > , ∣ Z − > |Z_{+}>,|Z_{-}> ∣Z+>,∣Z−> 两个本征态上,但是这两个本征态实际上是不可能直接观察到的,而我们“看见”的两束银原子,其实间接代表了两个具体的自旋磁矩的值,因为能使得银原子反生这种偏转的只能是收到了磁场力的作用,而这个力的来源 只能是其核外电子的自旋磁矩 μ \mu μ,所以按照这样解释的话,自旋磁矩的值就是这个这两个本征态的本征值。

请叫我 当代福尔摩斯,谢谢!!
(2)氢原子能级.
这个不光要回忆线性代数了,在这个关键的时刻,高中物理的底子才是我们取胜的法宝。
前面我们介绍了算符这个概念,在这里,我们继续学习一种能量算符,它在量子力学中的正式名称叫作哈密顿算符(Hamiltonian),记作 H ^ \widehat{H} H 。
在有势能束缚的条件下(可以简单理解为由于原子核和核外电子相互之间的引力势能),它也对应着一组离散的本征值和本征态,这就是我们熟悉的能级。
注意前方高能!注意调整心态!
将哈密顿算符作用在某个态矢量 ∣ ψ > |\psi > ∣ψ>上时,就可以写成: H ^ ∣ ψ > = E ∣ ψ > \widehat{H}|\psi > = E|\psi> H ∣ψ>=E∣ψ>.
而在数轴坐标中, H ^ \widehat{H} H 可以表示为:
H ^ = − h 2 2 m ∂ 2 ∂ x 2 + V ( x ) \widehat{H} = -\frac{h^{2}}{2m} \frac{\partial ^{2}}{\partial x^{2}} + V(x) H =−2mh2∂x2∂2+V(x)
其中V(x)代表总势能。。这个不理解不要紧,因为目前我也不理解 记住它的完事了,奥利给!!!
我们将 H ^ \widehat{H} H 带入第一个式子得:
[ − h 2 2 m ∂ 2 ∂ x 2 + V ( x ) ] ∣ ψ > = E ∣ ψ > [ -\frac{h^{2}}{2m} \frac{\partial ^{2}}{\partial x^{2}} + V(x)] |\psi > = E |\psi > [−2mh2∂x2∂2+V(x)]∣ψ>=E∣ψ>
这个时候,我们用函数 ψ ( x , t ) \psi(x,t) ψ(x,t)来代替态矢量 ∣ ψ > |\psi > ∣ψ>,这个函数叫波函数,非常重要,我们日后再叙。。。
[ − h 2 2 m ∂ 2 ∂ x 2 + V ( x ) ] ψ ( x , t ) = E ψ ( x , t ) [ -\frac{h^{2}}{2m} \frac{\partial ^{2}}{\partial x^{2}} + V(x)] \psi(x,t) = E \psi(x,t) [−2mh2∂x2∂2+V(x)]ψ(x,t)=Eψ(x,t)
这么一大坨的名字叫定态薛定谔方程。
在经过一些公式的替换和计算可以得到:
[ − h 2 μ 1 r 2 ∂ ∂ r ( r 2 ∂ ∂ r ) + L ^ 2 2 μ r 2 − 1 4 π ϵ 0 e 2 r ] ψ = E ψ [-\frac{h}{2\mu } \frac{1}{r^{2}} \frac{\partial }{\partial r}(r^{2} \frac{\partial }{\partial r}) + \frac{\widehat{L}^{2}}{2\mu r^{2}} - \frac{1}{4\pi\epsilon _{0} }\frac{e^{2}}{r}] \psi =E\psi [−2μhr21∂r∂(r2∂r∂)+2μr2L 2−4πϵ01re2]ψ=Eψ
左边那一大串其实就是替换了的 H ^ \widehat{H} H ,只是看起来比较复杂,不懂也没有关系。。
通过这个方程解出来的 ψ n \psi _{n} ψn其实就是哈密顿算符的本征态 ∣ E n > |E_{n}> ∣En>,而每个本征态对应的本征值 E n E_{n} En,就是我们熟知的氢原子能级了.
其实作为一名计科的学生,这么复杂的公式我是没看懂的,但是我们只需要理解这些公式背后所代表的意义和解的含义即可。。
好了,本次博客所要讲的内容就这么多了,不要忘记用您发财的小手指点一点 关注,点不了上当,点不了吃亏,祝您身体健康,万事如意~~