2021秋招-数据结构-二叉树相关
leetcode 树相关
⭐LeetCode刷题总结-树篇(上)
在LeetCode的标签分类题库中,和树有关的标签有:树(123道题)、字典树(17道题)、线段树(11道题)、树状数组(6道题)。对于这些题,作者在粗略刷过一遍后,对其中的考点进行了总结,并归纳为以下四大类:
一、 树基本特性问题
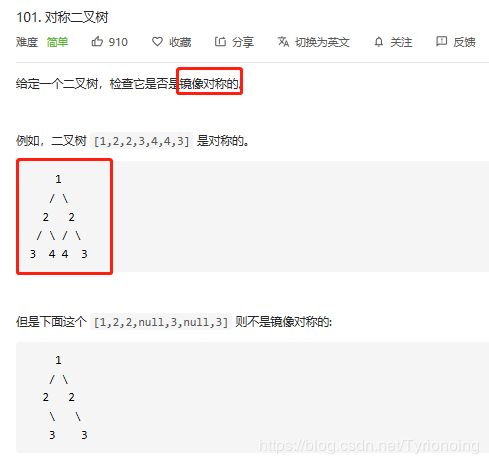
1. lc-101-对称二叉树-简单
- 思路1: 递归思路 : 深度优先遍历
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def isSymmetric(self, root: TreeNode) -> bool:
# 递归思路
def isMirror(root1, root2):
'''
判断两个二叉树是否镜像对称
'''
# 情况1: 如果 左右子树都为空,则这两个树镜像对称
if not root1 and not root2:
return True
# 情况2: 如果左右子树 一空、一不空,则这两个树不镜像对称
if not root1 or not root2:
return False
# 交给框架
return root1.val == root2.val and isMirror(root1.left, root2.right) and isMirror(root1.right, root2.left)
# 根节点做点什么
if not root:
return True
# 交给框架
return isMirror(root.left, root.right)
- 思路2:迭代思路: 层次遍历
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def isSymmetric(self, root: TreeNode) -> bool:
# 迭代思路: 层次遍历, 判断是否每层对称; 本质还是二叉树层次遍历;
queue = [root]
while queue:
# 记录二叉树层次的节点
res = []
queue_len = len(queue)
for i in range(queue_len):
curNode = queue.pop(0)
# 结果存储
if curNode:
res.append(curNode.val)
else:
res.append('None')
# 当前元素相邻节点添加
if curNode:
queue.append(curNode.left)
queue.append(curNode.right)
reverse_res = res[::-1]
if res != reverse_res:
return False
return True
[2.翻转二叉树以匹配前序遍历]
[3. leetcode-655输出二叉树-中等]
4. leetcode-617-合并二叉树
- 深度优先搜索
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def mergeTrees(self, t1: TreeNode, t2: TreeNode) -> TreeNode:
# 解题思路: 选取其中一个根节点作为返回值的根节点。
# 然后利用深度优先搜索的思想, 采用相同顺序同时遍历两棵树, 如果当前节点均存在则相加,
# 否则则选取g含有值的节点
if not t1:
return t2
if not t2:
return t1
t1.val = t1.val + t2.val
t1.left = self.mergeTrees(t1.left, t2.left)
t1.right = self.mergeTrees(t1.right, t2.right)
return t1
[5. leetcode-814-二叉树剪枝]
6.leetcode-199-二叉树的右视图-中等
- 解题思路:
层次遍历的实际应用。只需依次保存每层最右边的一个节点即可。 - 具体代码:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def rightSideView(self, root: TreeNode) -> List[int]:
if not root:
return []
queue = [root]
res = []
while queue:
res_line = []
queue_len = len(queue)
for i in range(queue_len):
curNode = queue.pop(0)
res_line.append(curNode.val)
if curNode.left:
queue.append(curNode.left)
if curNode.right:
queue.append(curNode.right)
res.append(res_line[-1])
return res
7. leetcode-111-二叉树的最小深度-简单
- 层次遍历思路:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def minDepth(self, root: TreeNode) -> int:
# BFS: 时间复杂度相对DFS较低, 但是空间复杂度O(N) > DFS:O(log N)
if not root:
return 0
queue = [root] # BFS使用队列
depth = 1 # 初始化高度/深度
while queue:
# 记录队列中元素数量: 二叉树每一层node数量
queue_size = len(queue)
# 遍历二叉树一层node, 并将周围节点加入 队列
for i in range(queue_size):
# 取最先进入队列元素
curNode = queue.pop(0)
# 判断是否到达终点
if not curNode.left and not curNode.right:
return depth
# 将当前节点周围node加入队列
if curNode.left:
queue.append(curNode.left)
if curNode.right:
queue.append(curNode.right)
# 遍历一层, 深度 +1
depth += 1
- 深度优先搜索思路
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def minDepth(self, root: TreeNode) -> int:
# root做点什么?
if not root:
return 0
# 交给框架
# 如果root左右子树都有,则选择最低深度
if root.left and root.right:
return 1 + min(self.minDepth(root.left), self.minDepth(root.right))
else:
return 1 + self.minDepth(root.left) + self.minDepth(root.right)
104. 二叉树的最大深度
- 递归思路:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def maxDepth(self, root: TreeNode) -> int:
if not root:
return 0
return max(self.maxDepth(root.left), self.maxDepth(root.right)) + 1
- 层次遍历思路: 累加
[8.leetcode-662-二叉树的最大宽度-中等]
[9.leetcode-543-二叉树的直径]
二、构造二叉树
[1. leetcode-889依据前序和后序遍历构造二叉树-中等]
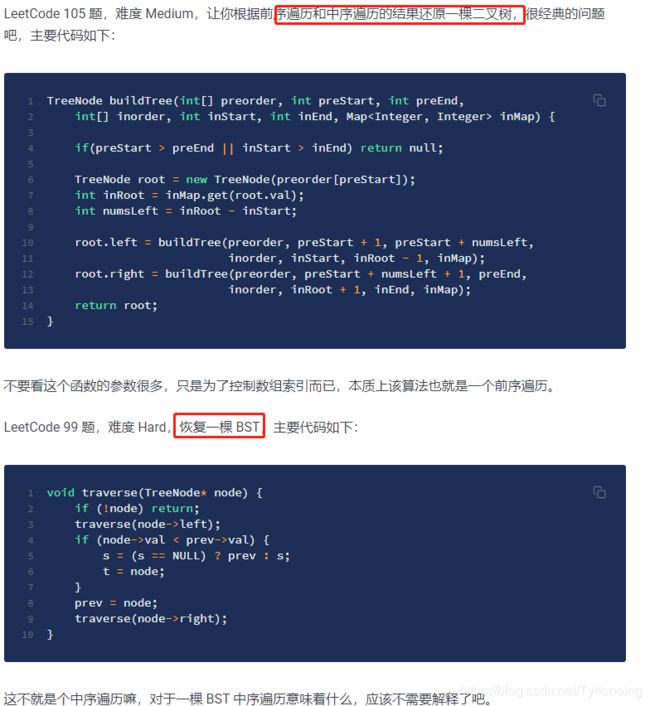
[2. leetcode-1028-从先序遍历还原二叉树-困难]
三、节点问题 11-16
[1. leetcode-236-二叉树的最近公共祖先-中等]
[2. leetcode-337-打家劫舍 III-中等]
[3. leetcode-623-在二叉树中增加一行-中等]
[4. leetcode-863-二叉树中所有距离为K的节点-中等]
[5. lc-968-监控二叉树-困难]
[6.lc-1145-二叉树着色游戏-中等]
四、路径问题
[1. lc-257-二叉树的所有路径-简单]
[2. lc-979-二叉树中分配硬币-中等]
[3.lc-987-二叉树的垂序遍历-中等]
[4.lc-124-二叉树中的最大路径和-困难]
[5.lc-437-路径总和 |||-简单]
二叉树的路径问题总结
112. 路径总和
113. 路径总和 II
437. 路径总和 III
257. 二叉树的所有路径
剑指 Offer 34. 二叉树中和为某一值的路径
1457. 二叉树中的伪回文路径
124. 二叉树中的最大路径和
687. 最长同值路径
1372. 二叉树中的最长交错路径
字节搜索面试:最大路径总和
框架
通过对以上问题的总结,对于二叉树的路径问题有个 屡试不爽 的框架,所有题目都可由该框架求得。可先浏览一下该框架,后面习题代码再对比一下。基本上题解就是填这个框架。
class Solution(object):
def maxPath(self, root, sum):
def dfs(head,path,target):
'''
dfs传入的head必须为非None
dfs由三部分组成 :
1、满足要求的处理
2、左右子树的处理
3、返回结果
'''
if not head.right and not head.left and ###:
# 满足要求做处理
return
if head.left:
# 对左子树dfs
if head.right:
# 对右子树dfs
return ###
####保证传入非None
if not root:
return ###
####调用dfs
dfs(root,[head.val],root.val)
return ###
112、路径总和
class Solution(object):
def hasPathSum(self, root, sum):
def dfs(head, target):
####dfs分三部分,非常简单
if target==sum and not head.right and not head.left:
return True
if head.right:
if dfs(head.right, target+head.right.val):
return True
if head.left:
if dfs(head.left, target+head.left.val):
return True
return False
if not root:
return False
return dfs(root, root.val)
113.路径总和2
class Solution(object):
def pathSum(self, root, sum):
res = []
def dfs(path,head,target):
# path 用于记录路径
#同样分为三部分
if target==sum and not head.right and not head.left:
res.append(path[:])
return
if head.left:
#因为这里要记录路径,回溯这一步不能少
path.append(head.left.val)
dfs(path,head.left,target+head.left.val)
path.pop()
if head.right:
path.append(head.right.val)
dfs(path,head.right,target+head.right.val)
path.pop()
if not root:
return []
dfs([root.val],root,root.val)
return res
-
路径总和3
与113的差别主要是:起点、终点没有限制。
代码主要在这两点上进行更改。
class Solution(object):
def pathSum(self, root, sum):
self.res = 0
def dfs(head,target):
# 终点没有限制,就不管它是否是叶子节点,即是否有左右叶子节点
if target == sum:
self.res += 1
if head.right:
dfs(head.right,target+head.right.val)
if head.left:
dfs(head.left,target+head.left.val)
if not root:
return 0
# 起点没有限制,那就把所有节点都作为起点试验一下
# 这里用到bfs
queue = [root]
while queue:
head = queue.pop()
dfs(head,head.val)
if head.right:
queue.append(head.right)
if head.left:
queue.append(head.left)
return self.res
-
二叉树的所有路径
很简单,注意细节就好
class Solution(object):
def binaryTreePaths(self, root):
res = []
def dfs(path,head):
if not head.right and not head.left:
res.append('->'.join(str(i) for i in path))
return
if head.right:
path.append(head.right.val)
dfs(path,head.right)
path.pop()
if head.left:
path.append(head.left.val)
dfs(path,head.left)
path.pop()
if not root:
return []
dfs([root.val], root)
return res
-
二叉树中的伪回文路径
这里伪回文是指,元素重新排列组合,可以是回文。回文有个特点,就是最多有一个字符的个数为奇数。
这里就可以使用hashmap来记录各各字母的个数。因为涉及路径,其实这里的hashmap起到的作用其实就是也给带计数的path.
class Solution(object):
def __init__(self):
self.res = 0
def pseudoPalindromicPaths (self, root):
"""
:type root: TreeNode
:rtype: int
"""
hashmap = collections.defaultdict(int)
def check(hashmap):
# 用于判断是否为回文
odd = 0
for _, cnt in hashmap.items():
if cnt%2 != 0:
odd += 1
if odd > 1:
return False
return True
def dfs(head):
# 如果为叶节点,判断是否为回文路径。这里不需要传入path,全局变量hashmap作为path
if not head.right and not head.left:
if check(hashmap):
self.res += 1
return
if head.right:
# 因为涉及路径,所以也要回退。这是是对hashmap回退
hashmap[head.right.val] += 1
dfs(head.right)
hashmap[head.right.val] -= 1
if head.left:
hashmap[head.left.val] += 1
dfs(head.left)
hashmap[head.left.val] -= 1
# 不需要return
if not root:
return 0
hashmap[root.val] += 1
dfs(root)
return self.res
-
二叉树中的最大路径和
注意:这里重新定义了路径和,和前面不同。
要求出最大路径和,一个简单的方法就是求出所有路径和,选出最大的。我们以某一节点为根节点,并且要求该根节点对应的最大路径必须过该根节点,这样遍历所有的节点,也就是遍历了所有可能的最大路径。
注意这里的路径和112、113中的路径不同,这个路径不是一路向下的,所以不能简单的用二分递归分治。原因就是根节点的最优路径和左右子节点的最优路径没有简单的相加关系。
解决方案就是,把这里的路径换算成同112、113中的路径,设这里的路径和为 F , 112,113中的路径和为 f ,则有: F(根节点) = max(f(左孩子),0 ) max(f(右孩子),0 )+ 根节点.val
而 f(根节点) = max(f(左孩子),f(右孩子),0 ) + 根节点.val
所以具有最优子结构的是 f 路径。所以这里dfs是对f路径进行的。
注意,其实这里用的的递归分治的dfs,所以和上面的回溯dfs函数有些不同。
class Solution(object):
def maxPathSum(self, root):
self.res = float('-inf')
#dfs()用于计算以head为根节点 f(head)
def dfs(head):
left, right = 0, 0
if head.left:
left = max(dfs(head.left), 0)
if head.right:
right = max(dfs(head.right), 0)
#计算以head为根节点的最大路径,更新最大值
self.res = max(self.res, left+right+head.val)
#注意这里返回的是 f(head)
return max(right,left) + head.val
if not root:
return 0
dfs(root)
return self.res
687 .最长同值路径
注意这里的路径和 124 是一样的,所以道题思路也是一致的
class Solution(object):
def longestUnivaluePath(self, root):
self.res = 1
def dfs(head):
right_cnt, left_cnt = 0, 0
if head.left:
left = dfs(head.left)
if head.left.val == head.val:
left_cnt += left
if head.right:
right = dfs(head.right)
if head.right.val == head.val:
right_cnt += right
self.res = max(self.res, right_cnt+left_cnt+1)
#返回以head为起点的最大值
return max(right_cnt,left_cnt) + 1
if not root:
return 0
dfs(root)
return self.res - 1
-
二叉树中的最长交错路径
因为存在左右交错,所以对于每个节点一定需要两个变量来分别代表左和右。并且,左、右要交错互换。
这里的左、右分别表示该节点左、右交错路径的长度。并且同一个节点,左右交错路径长度最多一个非零。
class Solution(object):
def longestZigZag(self, root):
self.res = 0
def dfs(head, left, right):
self.res = max(self.res, left, right)
# 因为是交互路径,左右要交互。注意对于一个节点,最多只有左、右中一个非零。
if head.left:
dfs(head.left, right+1, 0)
if head.right:
dfs(head.right, 0, left+1)
if not root:
return -1
dfs(root, 0, 0)
return self.res
字节搜索面试:最大路径总和
这道题背景和 437 一样,不同点是要求出最大路径和。因为这个变化,我们不需要像 437 一样使用BFS+DFS的方法,只需要DFS即可。想法和 124 一样,只是更简单了。
这里我们不需要路径和 F , 只需要路径和为 f ,所以只需要一下公式:
f(根节点) = max(f(左孩子),f(右孩子),0 ) + 根节点.val
这是递归的一种写法,f(根节点)即是以根节点作为起点,同样,我们可以设g(根节点)为以根节点作为结束点,这样dfs过程中就不需要递归了。
f(根节点)= max(f(父节点),0) + 根节点.val
总结
对于该框架重点包括:
dfs传入的head必须为非None
dfs由三部分组成 :
1、满足要求的处理
2、左右子树的处理
3、返回结果
二叉树的路径问题总结
112. 路径总和
113. 路径总和 II
437. 路径总和 III
257. 二叉树的所有路径
剑指 Offer 34. 二叉树中和为某一值的路径
1457. 二叉树中的伪回文路径
124. 二叉树中的最大路径和
687. 最长同值路径
1372. 二叉树中的最长交错路径
字节搜索面试:最大路径总和
框架
通过对以上问题的总结,对于二叉树的路径问题有个 屡试不爽 的框架,所有题目都可由该框架求得。可先浏览一下该框架,后面习题代码再对比一下。基本上题解就是填这个框架。
class Solution(object):
def maxPath(self, root, sum):
def dfs(head,path,target):
'''
dfs传入的head必须为非None
dfs由三部分组成 :
1、满足要求的处理
2、左右子树的处理
3、返回结果
'''
if not head.right and not head.left and ###:
# 满足要求做处理
return
if head.left:
# 对左子树dfs
if head.right:
# 对右子树dfs
return ###
####保证传入非None
if not root:
return ###
####调用dfs
dfs(root,[head.val],root.val)
return ###
112、路径总和
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-0WtykroD-1595903287543)(C:\Users\lenovo\AppData\Roaming\Typora\typora-user-images\image-20200724122621304.png)]
class Solution(object):
def hasPathSum(self, root, sum):
def dfs(head, target):
####dfs分三部分,非常简单
if target==sum and not head.right and not head.left:
return True
if head.right:
if dfs(head.right, target+head.right.val):
return True
if head.left:
if dfs(head.left, target+head.left.val):
return True
return False
if not root:
return False
return dfs(root, root.val)
113.路径总和2
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-pclaPcrn-1595903287547)(C:\Users\lenovo\AppData\Roaming\Typora\typora-user-images\image-20200724123420139.png)]
class Solution(object):
def pathSum(self, root, sum):
res = []
def dfs(path,head,target):
# path 用于记录路径
#同样分为三部分
if target==sum and not head.right and not head.left:
res.append(path[:])
return
if head.left:
#因为这里要记录路径,回溯这一步不能少
path.append(head.left.val)
dfs(path,head.left,target+head.left.val)
path.pop()
if head.right:
path.append(head.right.val)
dfs(path,head.right,target+head.right.val)
path.pop()
if not root:
return []
dfs([root.val],root,root.val)
return res
-
路径总和3
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-UgbtYASz-1595903287550)(C:\Users\lenovo\AppData\Roaming\Typora\typora-user-images\image-20200724124427093.png)]
与113的差别主要是:起点、终点没有限制。
代码主要在这两点上进行更改。
class Solution(object):
def pathSum(self, root, sum):
self.res = 0
def dfs(head,target):
# 终点没有限制,就不管它是否是叶子节点,即是否有左右叶子节点
if target == sum:
self.res += 1
if head.right:
dfs(head.right,target+head.right.val)
if head.left:
dfs(head.left,target+head.left.val)
if not root:
return 0
# 起点没有限制,那就把所有节点都作为起点试验一下
# 这里用到bfs
queue = [root]
while queue:
head = queue.pop()
dfs(head,head.val)
if head.right:
queue.append(head.right)
if head.left:
queue.append(head.left)
return self.res
-
二叉树的所有路径
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-eZbZZ0DH-1595903287552)(C:\Users\lenovo\AppData\Roaming\Typora\typora-user-images\image-20200724130637695.png)]
很简单,注意细节就好
class Solution(object):
def binaryTreePaths(self, root):
res = []
def dfs(path,head):
if not head.right and not head.left:
res.append('->'.join(str(i) for i in path))
return
if head.right:
path.append(head.right.val)
dfs(path,head.right)
path.pop()
if head.left:
path.append(head.left.val)
dfs(path,head.left)
path.pop()
if not root:
return []
dfs([root.val], root)
return res
-
二叉树中的伪回文路径
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-eBr1znV5-1595903287554)(C:\Users\lenovo\AppData\Roaming\Typora\typora-user-images\image-20200724134556037.png)]
这里伪回文是指,元素重新排列组合,可以是回文。回文有个特点,就是最多有一个字符的个数为奇数。
这里就可以使用hashmap来记录各各字母的个数。因为涉及路径,其实这里的hashmap起到的作用其实就是也给带计数的path.
class Solution(object):
def __init__(self):
self.res = 0
def pseudoPalindromicPaths (self, root):
"""
:type root: TreeNode
:rtype: int
"""
hashmap = collections.defaultdict(int)
def check(hashmap):
# 用于判断是否为回文
odd = 0
for _, cnt in hashmap.items():
if cnt%2 != 0:
odd += 1
if odd > 1:
return False
return True
def dfs(head):
# 如果为叶节点,判断是否为回文路径。这里不需要传入path,全局变量hashmap作为path
if not head.right and not head.left:
if check(hashmap):
self.res += 1
return
if head.right:
# 因为涉及路径,所以也要回退。这是是对hashmap回退
hashmap[head.right.val] += 1
dfs(head.right)
hashmap[head.right.val] -= 1
if head.left:
hashmap[head.left.val] += 1
dfs(head.left)
hashmap[head.left.val] -= 1
# 不需要return
if not root:
return 0
hashmap[root.val] += 1
dfs(root)
return self.res
-
二叉树中的最大路径和
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-xhucHv3G-1595903287559)(C:\Users\lenovo\AppData\Roaming\Typora\typora-user-images\image-20200724202801723.png)]
注意:这里重新定义了路径和,和前面不同。
要求出最大路径和,一个简单的方法就是求出所有路径和,选出最大的。我们以某一节点为根节点,并且要求该根节点对应的最大路径必须过该根节点,这样遍历所有的节点,也就是遍历了所有可能的最大路径。
注意这里的路径和112、113中的路径不同,这个路径不是一路向下的,所以不能简单的用二分递归分治。原因就是根节点的最优路径和左右子节点的最优路径没有简单的相加关系。
解决方案就是,把这里的路径换算成同112、113中的路径,设这里的路径和为 F , 112,113中的路径和为 f ,则有: F(根节点) = max(f(左孩子),0 ) max(f(右孩子),0 )+ 根节点.val
而 f(根节点) = max(f(左孩子),f(右孩子),0 ) + 根节点.val
所以具有最优子结构的是 f 路径。所以这里dfs是对f路径进行的。
注意,其实这里用的的递归分治的dfs,所以和上面的回溯dfs函数有些不同。
class Solution(object):
def maxPathSum(self, root):
self.res = float('-inf')
#dfs()用于计算以head为根节点 f(head)
def dfs(head):
left, right = 0, 0
if head.left:
left = max(dfs(head.left), 0)
if head.right:
right = max(dfs(head.right), 0)
#计算以head为根节点的最大路径,更新最大值
self.res = max(self.res, left+right+head.val)
#注意这里返回的是 f(head)
return max(right,left) + head.val
if not root:
return 0
dfs(root)
return self.res
687 .最长同值路径
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-LOnudcE5-1595903287561)(C:\Users\lenovo\AppData\Roaming\Typora\typora-user-images\image-20200724130243645.png)]
注意这里的路径和 124 是一样的,所以道题思路也是一致的
class Solution(object):
def longestUnivaluePath(self, root):
self.res = 1
def dfs(head):
right_cnt, left_cnt = 0, 0
if head.left:
left = dfs(head.left)
if head.left.val == head.val:
left_cnt += left
if head.right:
right = dfs(head.right)
if head.right.val == head.val:
right_cnt += right
self.res = max(self.res, right_cnt+left_cnt+1)
#返回以head为起点的最大值
return max(right_cnt,left_cnt) + 1
if not root:
return 0
dfs(root)
return self.res - 1
-
二叉树中的最长交错路径
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-eOft1HMk-1595903287563)(C:\Users\lenovo\AppData\Roaming\Typora\typora-user-images\image-20200724211113192.png)]
因为存在左右交错,所以对于每个节点一定需要两个变量来分别代表左和右。并且,左、右要交错互换。
这里的左、右分别表示该节点左、右交错路径的长度。并且同一个节点,左右交错路径长度最多一个非零。
class Solution(object):
def longestZigZag(self, root):
self.res = 0
def dfs(head, left, right):
self.res = max(self.res, left, right)
# 因为是交互路径,左右要交互。注意对于一个节点,最多只有左、右中一个非零。
if head.left:
dfs(head.left, right+1, 0)
if head.right:
dfs(head.right, 0, left+1)
if not root:
return -1
dfs(root, 0, 0)
return self.res
字节搜索面试:最大路径总和
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-sPWmBOIu-1595903287564)(C:\Users\lenovo\AppData\Roaming\Typora\typora-user-images\image-20200724215238490.png)]
这道题背景和 437 一样,不同点是要求出最大路径和。因为这个变化,我们不需要像 437 一样使用BFS+DFS的方法,只需要DFS即可。想法和 124 一样,只是更简单了。
这里我们不需要路径和 F , 只需要路径和为 f ,所以只需要一下公式:
f(根节点) = max(f(左孩子),f(右孩子),0 ) + 根节点.val
这是递归的一种写法,f(根节点)即是以根节点作为起点,同样,我们可以设g(根节点)为以根节点作为结束点,这样dfs过程中就不需要递归了。
f(根节点)= max(f(父节点),0) + 根节点.val
总结
对于该框架重点包括:
dfs传入的head必须为非None
dfs由三部分组成 :
1、满足要求的处理
2、左右子树的处理
3、返回结果
⭐LeetCode刷题总结-树篇(中)
一、 二叉树搜索树
[1. lc-95.不同的二叉搜索树 II-中等]
[2. lc-99.恢复二叉搜索树-困难 ]
[3. lc-450.删除二叉搜索树中的节点-中等]
[4. lc-701.二叉搜索树中的插入-中等]
二、平衡二叉树
[1. lc-110.平衡二叉树-简单]
三、满二叉树
[1. lc-894.所有可能的满二叉树-中等]
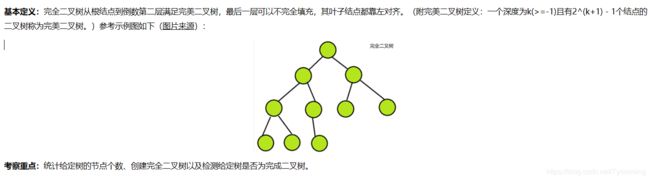
四、完全二叉树
[1. 222.完全二叉树的节点个数-中等(考察统计节点个数)]
[2. 919-919.完全二叉树插入器-中等(考察创建完全二叉)]
[3. 958.二叉树的完全性检验-中等(考察检测是否为完全二叉树)]
五、线段树
六、字典树
[1. 208.实现Trie(前缀树)-中等(考察创建字典树)]
[2. 212.单词搜索II-困难(考察单词搜索)]
[3. 648.单词替换-中等(考察单词搜索)]
七、树状数组
⭐LeetCode刷题总结-树篇(下)
一、新概念定义问题
[1. 117.填充每个节点的下一个右侧节点指针II-中等]
[2. 297.二叉树的序列化与反序列化-困难]
[3. 114.二叉树展开为链表-中等]
[4. 998.最大二叉树II-中等]
[5. 834.树中距离之和-困难]
二、子树问题
[1. 508.出现次数最多的子树元素和-中等]
[2. 652.寻找重复的子树-中等]
[3. 865.具有所有最深结点的最小子树-中等]
[4.1110.删点成林-中等]
LeetCode刷题–二叉树相关
LeetCode大佬总结: 二叉树 先序、中序、后续 三种非递归遍历
旧思路三种遍历统一框架
二叉树的遍历都可以借助栈结构使用DFS算法完成。
首先是最简单的先序遍历,**父>左>右。**见144题 。
每次入栈前先将父节点加入结果列表,然后左节点入栈。
当左子树遍历完后,再遍历右子树。
先序遍历,父>左>右
# 先序遍历,父>左>右
class Solution:
def preorderTraversal(self, root: TreeNode) -> List[int]:
res = [] #结果列表
stack = [] #辅助栈
cur = root #当前节点
while stack or cur:
while cur: #一直遍历到最后一层
res.append(cur.val)
stack.append(cur)
cur = cur.left
top = stack.pop() #此时该节点的左子树已经全部遍历完
cur = top.right #对右子树遍历
return res
后序遍历,左>右>父
后序遍历,左>右>父。见145题 。
能不能借助先序遍历的思路来呢,我们将上面的顺序翻转过来得到,父>右>左。
所以现在可以按照之前的方法遍历,最后把结果翻转一下。
# 后序遍历,左>右>父
class Solution:
def postorderTraversal(self, root: TreeNode) -> List[int]:
res = []
stack = []
cur = root
while stack or cur:
while cur:
res.append(cur.val)
stack.append(cur)
cur = cur.right #先将右节点压栈
top = stack.pop() #此时该节点的右子树已经全部遍历完
cur = top.left #对左子树遍历
return res[::-1] #结果翻转
中序遍历, 左>父>右
中序遍历, 左>父>右。见94题 。
与先序遍历不同的是,出栈时才将结果写入列表。
class Solution:
def inorderTraversal(self, root: TreeNode) -> List[int]:
res = []
stack = []
cur = root
while stack or cur:
while cur:
stack.append(cur)
cur = cur.left
top = stack.pop() #此时左子树遍历完成
res.append(top.val) #将父节点加入列表
cur = top.right #遍历右子树
return res
递归实现三种遍历
# 先序遍历
def preorderTraversal(self, root: TreeNode) -> List[int]:
if not root:
return None
print(root.val)
self.preorderTraversal(root.left)
self.preorderTraversal(root.right)
# 中序遍历
def midOrder(root):
if not root:
return None
self.midOrder(root.left)
print(root.val)
self.midOrder(root.right)
# 后序遍历
def postOrder(root):
if not root:
return None
self.postOrder(root.left)
self.postOrder(root.right)
print(root.val)
python实现树形DP,一般都是后序遍历,理由上述
class Solution:
def rob(self, root: TreeNode) -> int:
return max(self.dp(root))
def dp(curRoot):
if not curRoot:
return [0, 0]
# 后序遍历
left = self.dp(curNode.left)
right = self.dp(curNode.right)
dp = [0, 0]
# dp[0]:以当前 node 为根结点的子树能够偷取的最大价值,规定 node 结点不偷
# dp[1]:以当前 node 为根结点的子树能够偷取的最大价值,规定 node 结点偷
dp[0] = max(left[0], left[1]) + max(right[0], right[1])
dp[1] = curRoot.val + left[0] + right[0]
新思路: 完全模仿递归,不变一行。秒杀全场,一劳永逸
完全模仿递归,不变一行。秒杀全场,一劳永逸
新思路
递归的本质就是压栈,了解递归本质后就完全可以按照递归的思路来迭代。
怎么压,压什么?压的当然是待执行的内容,后面的语句先进栈,所以进栈顺序就决定了前中后序。
我们需要一个标志区分每个递归调用栈,这里使用nullptr来表示。
具体直接看注释,可以参考文章最后“和递归写法的对比”。先序遍历看懂了,中序和后序也就秒懂。
先序遍历
# 先序遍历: 自己未看
def preorderTraversal(self, root: TreeNode) -> List[int]:
if root is None: return [] # 首先介入root节点
result = []
stack = [root]
while stack:
p = stack.pop() # 访问过节点弹出
if p is None:
p = stack.pop()
result.append(p.val)
else:
if p.right: # 右节点先压栈,最后处理
stack.append(p.right) # 先append的最后访问
if p.left:
stack.append(p.left)
stack.append(p) # 当前节点重新压栈(留着以后处理),因为先序遍历所以最后压栈
stack.append(None) # 在当前节点之前加入一个空节点表示已经访问过了
return result
中序遍历
# 中序遍历
else:
if p.right:
stack.append(p.right)
stack.append(p)
stack.append(None)
if p.left:
stack.append(p.left)
后序遍历
else:
stack.append(p)
stack.append(None)
if p.right:
stack.append(p.right)
if p.left:
stack.append(p.left)
二叉搜索树操作集锦
大佬笔记-二叉搜索树操作集锦
相关题目:
leetcode-100.相同的树
leetcode-450.删除二叉搜索树中的节点
leetcode-701.二叉搜索树中的插入操作
leetcode-700.二叉搜索树中的搜索
leetcode-98.验证二叉搜索树
二叉树算法的设计的总路线:明确一个节点要做的事情,然后剩下的事抛给框架。
void traverse(TreeNode root) {
// root 需要做什么?在这做。
// 其他的不用 root 操心,抛给框架
traverse(root.left);
traverse(root.right);
}
举两个简单的例子体会一下这个思路,热热身。
- 如何把二叉树所有的节点中的值加一?
void plusOne(TreeNode root) {
if (root == null) return;
root.val += 1;
plusOne(root.left);
plusOne(root.right);
}
# python
def plusOne(TreeNode root):
if root == None:
return None
root.val += 1
plusOne(root.left)
plusOne(root.right)
- 如何判断两棵二叉树是否完全相同?
leetcode-100. 相同的树-简单
100. 相同的树
给定两个二叉树,编写一个函数来检验它们是否相同。
如果两个树在结构上相同,并且节点具有相同的值,则认为它们是相同的。
示例 1:
输入: 1 1
/ \ / \
2 3 2 3
[1,2,3], [1,2,3]
输出: true
python题解
# python
def isSameTree(TreeNode root1, TreeNode root2):
# 如果都为空, 现然相同
if root1 == None and root2 == None:
return True
# 一个为空, 一个非空, 显然不同
if root1 == None or root2 == None:
return False
# 两个都非空, 但是 val不同,现然不同
if root1.val != root2.val:
return False
# root1, root2 该比的都比完了
return isSameTree(root1.left, root2.left) and isSameTree(root1.right, root2.right)
借助框架,上面这两个例子不难理解吧?如果可以理解,那么所有二叉树算法你都能解决。
二叉搜索树(Binary Search Tree,简称 BST)是一种很常用的的二叉树。它的定义是:一个二叉树中,任意节点的值要大于等于左子树所有节点的值,且要小于等于右边子树的所有节点的值。
如下就是一个符合定义的 BST:

下面实现 BST 的基础操作:判断 BST 的合法性、增、删、查。其中“删”和“判断合法性”略微复杂。
零、判断 BST 的合法性
leetcode-98. 验证二叉搜索树-中等
98. 验证二叉搜索树
给定一个二叉树,判断其是否是一个有效的二叉搜索树。
假设一个二叉搜索树具有如下特征:
节点的左子树只包含小于当前节点的数。
节点的右子树只包含大于当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。
示例 1:
输入:
2
/ \
1 3
输出: true
这里是有坑的, 按照刚才的思路, 每个节点自己要做的不就是比较自己和左右孩子嘛? 看起来代码:
def isVailsBST(TreeNode root):
# root 需要做什么?在这做。
if root == None:
return False
# 若: 根值 <= 左子树,返回False
if root.left and root.val <= root.left.val:
return False
# 若: 根值 >= 右子树, 返回False
if root.right and root.val >= root.right.val:
return False
# 其他的不用 root 操心,抛给框架
return isValidBST(root.left) and isValidBST(root.right)
!!! 但是这个算法出现了错误, BST的每个节点应该要小于 右边子树的所有节点,下面的二叉树现然不是 BST,但上述算法会误认为是。
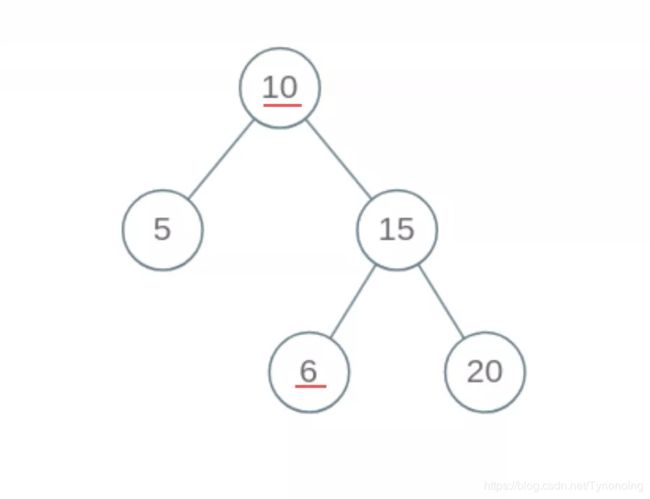
出现错误,不要慌张,框架没有错,一定是某个细节问题没注意到。我们重新看一下 BST 的定义,root 需要做的,不仅仅是和左右子节点比较,而是要和左子树和右子树的所有节点比较。怎么办,鞭长莫及啊!
这种情况,我们可以使用辅助函数,增加函数参数列表,在参数中携带额外信息,请看正确的代码:

python 最终AC版本代码
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def isValidBST(self, root: TreeNode) -> bool:
def isBST(root, minValue, maxValue):
# root 该做的事情
if not root:
return True
if minValue and root.val <= minValue.val:
return False
if maxValue and root.val >= maxValue.val:
return False
return isBST(root.left, minValue, root) and isBST(root.right, root, maxValue)
return isBST(root, None, None)
这样,root 可以对整棵左子树和右子树进行约束,根据定义,root 才真正完成了它该做的事,所以这个算法是正确的。
一、在 BST 中查找一个数是否存在
leetcode-700. 二叉搜索树中的搜索-简单
700. 二叉搜索树中的搜索
给定二叉搜索树(BST)的根节点和一个值。 你需要在BST中找到节点值等于给定值的节点。
返回以该节点为根的子树。 如果节点不存在,则返回 NULL。
例如,
给定二叉搜索树:
4
/ \
2 7
/ \
1 3
和值: 2
你应该返回如下子树:
2
/ \
1 3
根据我们的指导思想,可以这样写代码:
class Solution:
def searchBST(self, root: TreeNode, val: int) -> TreeNode:
# root做的事情
if not root or not val:
return None
if root.val == val:
return root
left = self.searchBST(root.left, val)
right = self.searchBST(root.right, val)
if left:
return left
if right:
return right
python实现: 注意利用 BST性质进行加速搜索
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def searchBST(self, root: TreeNode, val: int) -> TreeNode:
# root做的事情
if not root or not val:
return None
if root.val == val:
return root
if root.val > val:
left = self.searchBST(root.left, val)
return left
if root.val < val:
right = self.searchBST(root.right, val)
return right
一套针对 BST 的遍历框架:
def BST(root, target):
if root.val == target:
# 找到目标, 做点什么
if root.val < target:
BST(root.right, target)
if root.val > target:
BST(root.left, target)
二、在 BST 中插入一个数
leetcode-701. 二叉搜索树中的插入操作-中等
701. 二叉搜索树中的插入操
给定二叉搜索树(BST)的根节点和要插入树中的值,将值插入二叉搜索树。 返回插入后二叉搜索树的根节点。
保证原始二叉搜索树中不存在新值。
注意,可能存在多种有效的插入方式,只要树在插入后仍保持为二叉搜索树即可。 你可以返回任意有效的结果。
例如,
给定二叉搜索树:
4
/ \
2 7
/ \
1 3
和 插入的值: 5
你可以返回这个二叉搜索树:
4
/ \
2 7
/ \ /
1 3 5
或者这个树也是有效的:
5
/ \
2 7
/ \
1 3
\
4
对数据结构的操作无非 遍历 + 访问, 遍历就是‘找’, 访问就是‘改’。 具体到这个问题, 插入一个数, 就是先找到插入位置,然后进行插入操作。
上一个问题,总结了BST中的遍历框架, 就是 “找” 的问题。 直接 套上框架, 加上”改“的操作即可。 一旦涉及”改“, 函数就要返回TreeNode 类型, 并且对 递归调用的返回值进行接收。 (一定一定记住了。 )
python实现
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def insertIntoBST(self, root: TreeNode, val: int) -> TreeNode:
# root该做的事情
if not root:
return TreeNode(val)
# 框架做的事情
if root.val < val:
root.right = self.insertIntoBST(root.right, val)
if root.val > val:
root.left = self.insertIntoBST(root.left, val)
return root
三、在 BST 中删除一个数
leetcode-450. 删除二叉搜索树中的节点-中等
450. 删除二叉搜索树中的节点
给定一个二叉搜索树的根节点 root 和一个值 key,删除二叉搜索树中的 key 对应的节点,并保证二叉搜索树的性质不变。
返回二叉搜索树(有可能被更新)的根节点的引用。
一般来说,删除节点可分为两个步骤:
首先找到需要删除的节点;
如果找到了,删除它。
说明: 要求算法时间复杂度为 O(h),h 为树的高度。
示例:
root = [5,3,6,2,4,null,7]
key = 3
5
/ \
3 6
/ \ \
2 4 7
给定需要删除的节点值是 3,所以我们首先找到 3 这个节点,然后删除它。
一个正确的答案是 [5,4,6,2,null,null,7], 如下图所示。
5
/ \
4 6
/ \
2 7
另一个正确答案是 [5,2,6,null,4,null,7]。
5
/ \
2 6
\ \
4 7
python 初级版本实现
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def getMin(self, root):
# 右子树BST中的最小值
while root.left:
root = root.left
return root.val
def deleteNode(self, root: TreeNode, key: int) -> TreeNode:
# root做的事
if not root:
return None
if root.val == key:
# 情况1: key 左子树为空
if not root.left:
return root.right
# 情况2: key 右子树为空
if not root.right:
return root.left
# 情况3: key 左右子树都非空
minValue = self.getMin(root.right)
root.val = minValue
root.right = self.deleteNode(root.right, minValue)
# 搜索左子树
elif root.val > key:
root.left = self.deleteNode(root.left, key)
elif root.val < key:
root.right = self.deleteNode(root.right, key)
return root
删除操作就完成了。 注意一下,这个删除操作并不完美,因为我们一般不会通过 root.val = minNode.val 修改节点内部的值来交换节点, 而是通过一些列略微复杂的链表操作交换 root 和 minNode 两个节点。 因为具体的应用中, val 域可能会很大,修改起来耗时, 而链表操作无非改一下指针,而不会去碰内部数据。
但这里忽略这个细节, 旨在突出BST基本操作的共性,以及借助框架逐层细化问题的思维方式。
四、最后总结
通过这篇文章,你学会了如下几个技巧:
- 二叉树算法设计的总路线:把当前节点要做的事情做好,其他的交给框架,不用当前节点操心。
- 如果当前节点会对下面的子节点有整体影响,可以通过辅助函数增长参数列表,借助参数传递信息。
- 在二叉树框架之上,扩展出一套BST遍历框架:
def BST(TreeNode root, int target):
# 当前节点该做的事情
if root.val == target:
# 找到目标, 做点什么:
elif root.val < target:
BST(root.right, target)
elif root.val > target:
BST(root.left, target)
4.掌握BST的基本操作: 增、删、改、查。
模板总结篇
二叉树
def traverse(TreeNode root) :
// root 需要做什么?在这做。
// 其他的不用 root 操心,抛给框架
traverse(root.left);
traverse(root.right);